Matematik Dünyası dergisinin eski sayılarının birinde rastladım bu soruya. Geçtiğimiz Şubat’ta kaybettiğimiz Tosun Terzioğlu sormuş ve yanıtlamış. Kendisiyle yaptığım doyumsuz söyleşileri hüzünle hatırlayarak okuduğum Tosun Bey’in bu yazısından alıntıladığım bazı bölümleri Bilim ve Gelecek okurlarıyla paylaşmak istiyor, Tosun Bey’i saygı ve minnetle anıyorum.
“Bir matematikçi hayatta ne yapar?” diye sorulduğunda, “düşünür” derim. Matematikçi elbette ders verir, araştırma yapar, bunun için kitap okur, makale okur. Zaman zaman kâğıt kalemle çalışır, hesap yapar… Ama esas yaptığı bence, düşünmektir.
[…] Matematikle uğraştığım zaman karşılaştığım tanıdıklar zaman zaman sorarlardı, “hayrola, niye böyle düşünceli gözüküyorsun” diye. Doğru cevabım, “düşünceli gözüküyorum, çünkü düşünüyorum”, olmalıydı kuşkusuz. Ama genelde “düşüncesiz görünmemek için düşünceli gözüküyorum. Yoksa kötü bir durum yok” falan gibisinden cevap verirdim. Aslında çalışan bir matematikçiye, “düşünceli görünüyorsun” demekle on bin metre yarışında koşan bir atlete “nefes nefese kalmışsın, çok terliyorsun” demek arasında bir fark yok. Kaldı ki düşünmenin insan sağlığına zararlı bir etkisi olduğunu iddia eden bir doktora, doğrusu şimdiye kadar hiç rastlamadım!
[…] Tabii, salt düşünmek de yetmiyor. Okumak, yapılan araştırmaları takip edebilmek ve yaptığınız bir araştırma sonucunda bulduğunuz sonucu birtakım yerlerde anlatmak, başka meslektaşlarınızın eleştirisine sunmak… Çünkü matematik açık bir eylemdir. Yaptığınız şeyi kendinize saklayıp da sağda solda “ bakın ben neler yaptım neler, ama size anlatamam!” diye böbürlenirseniz, herkes sizden biraz kaçar veya size garip bir şekilde bakar, hatta “bu adam hasta mı acaba?” diye sorar.
Matematikte yeni bir şey yaptığınız zaman, ispatınızı olanca açıklığıyla ya bir bilimsel toplantıda anlatacaksınız veya makale olarak yazacaksınız. Anlatırken veya makalenizi yazarken hiçbir şeyi gizlemeyeceksiniz. Yaptığınız meslektaşlarınızca kontrol edilecek, doğru bulunacak, ondan sonra bu sizin yaptığınız şey tescil olmuş sayılacak.
[…] Bütün bu süreçlerde yaptığınızı kabul ettirmek veya beğendirmek için unvanınızı, pozisyonunuzu falan ortaya atmaktan kesinkes kaçınmalısınız. “Ben şöyle önemli bir kişiyim” veya “ geçmişte ne kadar ödül aldım” gibi laflarla ortaya çıkarsanız matematik toplumunda pek komik, hatta acıklı bir duruma düşersiniz. Çünkü burada büyüteç altında olan siz değilsiniz; büyüteç altındaki yaptığınız matematik. Matematikçiler kerameti matematikte ararlar, kişilerde değil!
Bana göre matematik, insanlığın tarihi boyunca küçük küçük taşları bir araya getirerek zekâsıyla inşa ettiği çok yüce bir anıt. Çağlar boyunca durmadan gelişen ve değişen bir anıt. Diyelim siz de makalenizi yayımlattınız ve anıta bir taş koydunuz; ümit edersiniz ki yıllar sonra o taşı oraya sizin koyduğunuz başkaları tarafından hatırlansın. Başka matematikçiler çıksın sizin koyduğunuz o taşın üzerine bir taş daha koysun. Bir matematikçinin en büyük ümidi ve düşü işte bundan ibarettir.
Matematik yorucu bir iştir… Matematik yaparken, özellikle araştırma yaparken insan kimi zaman hep aynı şeyleri düşünür durur. Başka birisinin yaptığı matematiği bile anlamak kolay değildir. Öyle bir roman okur gibi okuyamazsınız matematik makalesini, hatta bir ders kitabını. Zaman zaman zorlanırsınız, yorulursunuz. “Neden istediğim sonucu almıyorum?” diye sinirlenirsiniz. Kendinizi yıpratmaya başlarsınız. Yılgınlığa kapılmanız, matematiği bırakıp başka şeyle uğraşmayı düşünmeniz işten bile değildir.
Öyle durumlarda ben bırakırım düşündüğüm problemi, unuturum aylarca. Üzerine çalıştığım problemi tamamen bir kenara attığım da çok olur. Ama bazen de, eğer şansım yaver gider ve ilham perisi bana gülerse, birden aklıma yepyeni bir fikir gelir, geri dönerim ve o problemi kolaylıkla çözebilirim. Her şey takır takır yerli yerine oturur. Kafanızda aylarca dönüp dolaşan bulanık fikirler, belirsizlikler bir düzene kavuşur. Toz duman yatışır ve ortaya küçücük de olsa yalın, duru bir mantık yürütme ve güzel bir teorem çıkar.
İşte o anda ufuk çizgisindesiniz. Kimsenin daha önce bakmadığı yerleri görmektesiniz. Etrafta başka bir ayak izi yok. Matematiğin gizemli bahçesinin bir köşesindesiniz tek başınıza. Sessiz ama yoğun bir sevinçle dolusunuz. Böyle anlar ne kadar kısa sürerse sürsün, ne kadar az sıklıkta yaşanırsa yaşansın, belki de en büyük ödüldür bir matematikçi için. Tüm yorgunluklara değen, yol boyunca karşılaşılan zorlukları ve hayal kırıklarını unutturan böyle anlar sizi yeniler. Matematiği bırakmayı düşündüğünüz günleri hatırlayıp kendinize gülersiniz.
Ben matematikçi olmayı seçtim yıllar önce … İyi ki de böyle yapmışım!
Not: Matematik Dünyası dergisinin Aralık 2001 sayısında yayımlanan bu yazı Tosun Terzioğlu’nun 13 Eylül 2000’de Açık Radyo’daki konuşma metninden alıntılanmıştır.
Geçen sayıdaki soruların çözümü:
Birinci Soru. A, B, C, D, E, F harfleri 6×6’lık bir satranç tahtasına Şekil 1’deki gibi yerleştiriliyor. Kalan kareleri de A, B, C, D, E, F harfleriyle dolduracağız, ama her sütun ve her satırda bu harflerin tümü bulunmalı. Bu koşullara göre kalan karelere bu harfleri nasıl yerleştirebilirsiniz?
Çözüm:
İkinci Soru. Şekil 2’deki 7 kare sırayla 1’den 7’ye kadar numaralandırılmıştır. Şekildeki gibi 1, 2, 3 numaralı karelere beyaz, 5, 6 ve 7 numaralı karelere de siyah pullar koyuyoruz. Ortadaki 4 numaralı kare ise boş kalıyor. Amacımız, bütün beyaz pullarla siyah pulların yerlerini karşılıklı olarak değiştirmek, ama şu koşullarla: 1) Beyazları soldan sağa doğru, siyahları ise sağdan sola doğru hareket ettirebiliriz. 2) Bu hareketleri yaparken bir pulu, bulunduğu karenin bitişiğindeki boş kareye getirebiliriz veya zıt renkli bir pulun üstünden atlatıp boş bir kareye koyabiliriz. 3) Pulları, renklerine bakılmaksızın, herhangi bir düzende hareket ettirebiliriz.
Bu koşullara göre, en az sayıda hamle ile, beyaz ve siyah pulların yerlerini değiştirmek ( Şekil 2’deki beyaz pulları siyah pulların bulunduğu karelere, siyah pulları da beyaz pulların bulunduğu karelere taşımak) için pulların numaralarına göre hangi hareketleri yapmalıyız?
Çözüm: Başlangıçtan çözüme kadar aşağıda numaralarla gösterdiğimiz 15 hareket gerekmektedir.
3-4 5-3 6-5 4-6 2-4 1-2 3-1 5-3 7-5 6-7
4-6 2-4 3-2 5-3 4-5
Üçüncü Soru. Üzerlerine A, B, C, D harfleri yerleştirilmiş dört pul, Şekil 3’teki gibi taralı karelere koyulmuştur. Yapacağımız şey, C ile D’nin, A ile de B’nin yerlerini değiştirmek, ama şu koşullarla: 1) Pulları her hangi bir yönde bir veya birden fazla boş karenin üzerinden geçirebiliriz. Örneğin B pulunu saat yönünün tersinde hareket ettirerek, bir tur atıp A pulunun yanına getirebiliriz. 2) Herhangi bir pulu diğer bir pulun üstünden atlatarak hareket ettiremeyiz.
Bu koşullara göre C ile D’nin, A ile de B’nin yerlerini değiştirmek için hangi hareketleri yapmalıyız?
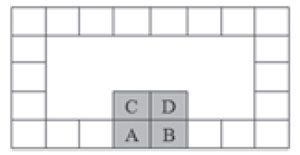Çözüm: A, B, C ve D pullarının bulunduğu karelere sırasıyla 1, 2, 3, 4 numaralarını verelim. İlk adım: B pulunu sağ yönde bir kare hareket ettirelim. Sonraki adım: A pulunu saat yönünde dairesel bir şekilde hareket ettirerek B pulunun sağındaki kareye getirelim. Şimdi de C ve D pullarının yerlerini değiştirmek için, soruda parantez içinde karelere verdiğimiz numaralara göre C ve D’ye şu hareketleri yaptıralım. Önce C: 3-1-2, sonra D: 4-3 ve ardından C: 2-4. Son olarak, B – A pullarını 1 ve 2 karelerinin yerlerine, yani sola doğru kaydıralım.
Dördüncü Soru. Bu problem, Şekil 4’te görüldüğü gibi aynı hat üzerinde bulunan A ve B trenlerinin yerlerinin değiştirilmesini konu etmektedir. Her iki trenin de ikişer vagonu ve birer lokomotifi vardır. Tüm vagonların uzunlukları eşittir. L-K-R ana hat olmak üzere, K kavşağından bir yan hat ayrılmaktadır. Yan hattın uzunluğu sadece bir vagonun uzunluğu kadardır. Bu durumda makinistler hangi manevraları yaparlarsa A treniyle B treninin yerleri değişmiş, yani B, A’nın arkasına geçmiş olur?
Çözüm: Trenlerin yaptığı hamleleri 6 adımda ifade edeceğiz. Adımları daha kolay takip edebilmek için şekil çizmenizi öneririm.
1) B trenini R yönünde ilerletip, K kavşağını geçerek L yönünde geriye doğru hareket ettirip, arka vagonunu yan hatta bırakarak ön vagonunu ana hatta çıkaralım.
2) Sadece ön vagonu bulunan B treni ana hat üzerinde L yönüne doğru geri geri götürerek A treninin lokomotifine bağlayalım ve arkasına A trenini alarak R yönünde ilerleyip K kavşağını geçelim.
3) Bu aşamada A trenin önüne B treninin ön vagonunun bağlı olduğunu ve bu trenlerin bu şekilde R yönünde bulunduklarını hatırlatalım. Şimdi bu trenleri belirttiğimiz biçimde (birbirlerine bağlı olarak) L yönüne doğru geri geri götürelim ve yan hatta bulunan B’nin arka vagonunu A’nın arkasına bağlayalım. Ardından bütün vagonlar birbirine bağlı şekilde (en arkada B’nin arka vagonu, arada A treni, önde de B’nin ön vagonu) trenleri R yönüne hareket ettirerek ana hatta çıkaralım ve sonra da geri geri hareket ettirerek K kavşağını geçip L yönüne götürelim.
4) B treninin lokomotifini ön vagonuyla birlikte konvoydan ayırıp R yönüne hareket ettirerek K kavşağını geçelim ve sonra da geri geri hareket ettirerek yan hatta ön vagonunu bırakalım, lokomotifi R yönünde ilerletelim.
5) A’yı B’nin arka vagonundan ayırarak K kavşağını geçelim, R yönünde ilerletelim ve geri geri L yönünde giderek yan hattan B’nin ön vagonunu alarak, ana hatta geri geri L yönünde gidelim. B’nin arka vagonuyla ön vagonunu birbirine bağlayalım.
6) B’nin lokomotifini R yönünden L yönüne doğru geri geri getirerek yan hatta koyalım ve A’yı K kavşağından geçirerek R yönünde ilerletelim. B’nin lokomotifini yan hattan çıkarıp, geri geri L yönünde götürerek ön vagonuna bağlayalım.
Beşinci Soru. Silindir şeklinde camdan yapılmış 6 litrelik iki kabımız var. Kaplardan ince ve uzun olanının yüksekliği 9 birim, kısa ve geniş olanının yüksekliği 4 birim. Ayrıca, büyük bir üçüncü kabımız var. Bir musluktan istediğimiz kadar su alabileceğimize göre 4 litre suyu nasıl ölçeriz?
Çözüm: Geçen sayıda bu sorunun son cümlesindeki “4” rakamı “6” olarak yazılmış, bu yanlışlık için özür dileyerek çözümü veriyoruz.
Kısa kabı cetvel olarak kullanıp, uzun kabı yüksekliğinin 5/9’una kadar doldururuz. Bu durumda elimizde 6 x 5/9=10/3 litre su olur. Sorasında, yine kısa kabı cetvel olarak kullanarak uzun kabın 1/9’u kadar miktarı kısa kaba boşaltırız. Böylece kısa kapta 6 x 1/9=2/3 litre su vardır. Uzun kabı tamamen boşaltıp, kısa kaptaki suyu üçüncü kaba dökeriz.
Bu işlemi 6 kez tekrar edince üçüncü kapta 2/3 x 6=4 litre su olur.
Altıncı Soru. İki arkadaş İzmir’den saat 6.00’da hareket ederek 6 saatte Bursa’ya varıyorlar.
Ertesi gün yine saat 6.00’da Bursa’dan İzmir’e hareket ederek 4 saat sonra İzmir’de oluyorlar. Aracın sürücüsü dönüş yolunda arkadaşına “Dün tam bu saatte buradaydık.” dediği anda saat kaçtı?
Çözüm: İzmir’den Bursa’ya gidişteki hız 2v ise dönüşteki hız 3v’dir. Bu durumda İzmir Bursa arasındaki yolu 12v olarak gösterebiliriz. “Dün tam bu saatte buradaydık” denildiği andaki saate t dersek aşağıdaki denklem yazabilir.
3v(t–6)+2v(t–6) = 12v
Buradan t=42/5=8,4 olur. O halde, “Dün tam bu saatte buradaydık” denildiği anda saat 8.24.
Yedinci Soru. Bir hekim 5 günde bir nöbet tutmaktadır. İlk nöbetini salı günü tutuyor, ama nöbet tutma sırası tekrar salıya rastladığında 4 günde bir nöbet tutmaya başlıyor. Sonraki nöbeti yine salıya geldiğinde 3 günde bir nöbet tutuyor. Bu şekilde, nöbet tutuğu her salı iki nöbet arasındaki süreyi 1 gün azaltıyor. Bu hekim kaç nöbet tutar?
Çözüm: Salı günü tuttuğu İlk nöbetten sonra 5 günde bir nöbet tutarak ilk kez tekrar salı günü nöbet tutabilmesi için 7 x 5 =35 gün geçmesi gerekir, yani ilk nöbetten sonra 7 nöbet tutarak yine ilk kez salı günü nöbet tutar. 4 günde bir nöbet tuttuğunda ise 7 x 4 =28 gün sonra yine salı günü nöbet tutar. Bu durumda da arada yine 7 nöbet tutacaktır, yani nöbetler arasındaki gün sayısı değişse de salıdan salıya 7 nöbet tutar. Bu şekilde düşündüğümüzde 7 x 5 =35, ilk nöbetle birlikte toplam 7 nöbet tutar.
Sekizinci Soru. Bir kuyrukta bulunan A, B ve C gibi üç kişiden A’nın B ile arasında 11, C ile arasında 15 kişi vardır. B ile C arasındaki kişi sayısı A’nın hem baştan hem sondan sıra sayısına eşitse C kaçıncı sırada olabilir?
Çözüm: Önce B ile C arasındaki kişi sayısına bakalım: İki seçenek var, ya 15 – 11 – 1 = 3 kişi, ya da 11 + 15 + 1 = 27 kişi. Eğer B ile C arasında 3 kişi olsaydı A’nın sırası 4, kuyrukta toplam 7 kişi olurdu ki bu sorunun verilenlerine uymuyor. O halde B ile C arasında 27 kişi var. Bu durumda A’nın sırası 27 ve kuyruktaki toplam kişi sayısı 53 olur. Demek ki C’nin sırası ya 10 ya da 44 olabilir.
