Gezegenlerin yörüngelerinin şeklini, Newton’un çekim yasası belirler diyebiliriz. Ama bunun keşfi pek kolay olmadı. Bütün kapalı yörüngeler (periyodik) genelde elips veya elipsin özel hali olan daire şeklindedir. Gökcisimlerinin yörüngelerinin şekilleri arasındaki farkların kaynağının ne olduğunun belirlenmesi için ise Einstein beklendi.
Soru 1- Gezegenlerin yörüngelerinin şeklini ne belirler?
Gezegenlerin yıldızlı gökyüzü üzerinde dolanımları, eski çağlardan beri insanların ilgisini çekmiştir. Gözlemlere göre, yıldızlar birbirlerine göre durumlarını koruyarak, yekpare bir kubbe gibi Yer’in çevresinde dönerken, gezegenler bazen ileri gidiyor, bazen geri kalıyor, bazen duraksıyor, dönemin bir gözlemcisinin deyimiyle, sinek gibi yıldızlar arasında dolaşıyorlardı. Gezegenlerin bu gizemli hareketlerini açıklamak için önerilen “bilimsel” diye niteleyebileceğimiz ilk çözüm, Platon’un önerisi üzerine, öğrencilerinden Eudoksus (MÖ 406-355) tarafından geliştirildi. Daha sonra, Platon’un diğer bir öğrencisi olan Aristoteles tarafından benimsenip en sonunda İskenderiyeli Ptolemaios tarafından geliştirilip son şeklini alan bu modellerin ortak özelliği, gezegen hareketlerinin dairesel veya dairesel hareketlerin bileşimi olmasıydı. Mistik eğilimleri ağır basan Platon’a göre, en kusursuz hareket dairesel olan idi ve her şeyin kusursuz olması gereken gökyüzünde, hareketler ancak dairesel olabilirdi. Bilimsel nedenlerden çok, değer yargılarına dayalı bu inanç, öylesine kök saldı ki, 2000 yıla yakın süre, gökbilimini egemenliği altında tuttu. Kopernik bile, ayaklarımızın altında sapasağlam ve kıpırdamadan durduğuna herkesin inandığı bir çağda, Yer’i, evrenin tümü sanılan gezegenler sisteminin merkezinden alıp, Güneş çevresinde dolanan sıradan bir gezegen durumuna indirmeyi göze aldığı halde, dairesel hareketlerden vazgeçmeye bir türlü cesaret edememiştir.
17. yüzyıla gelindiğinde, Kopernik kuramı hâlâ tartışma konusu idi. Danimarkalı astronom Tycho-Brahe 1601’de öldüğü zaman, uzun yıllardan beri biriktirmiş olduğu gezegen gözlemlerinin verileri, asistanı Johannes Kepler’in eline geçti. Bu paha biçilmez mirası sahiplenen genç Alman astronom, ilgisini özellikle Mars gezegenine odaklayarak, yıllar süren uzun bir çalışma sonunda, bu gezegenin yörüngesinin, sanıldığı gibi dairesel olmayıp, odaklarından birinde Güneş’in bulunduğu bir elips olduğunu kanıtladı. Kepler’in elde etmiş olduğu bu sonuca, Kepler’in birinci yasası denmektedir. Bu bir devrim niteliğinde idi. İki bin yıllık dairesel yörünge egemenliği sona ermişti.
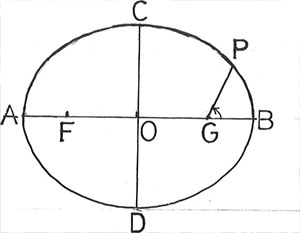
Elips nedir? Elips ile daire arasındaki fark nedir? Kısaca hatırlatalım. Daire, bir düzlem üzerinde seçilen belirli bir noktadan sabit uzaklıktaki noktaların geometrik yeridir. Bu sabite, dairenin yarıçapı denir. Elips ise, bir düzlem üzerinde seçilen ve elipsin odakları denilen iki ayrık noktadan, uzaklıklarının toplamı sabit olan noktaların geometrik yeridir. Bir odağı F olan, diğer odağı G’de ise Güneş’in bulunduğu bir elips göz önüne alalım (Şekil 1). P ise, yörünge üzerindeki gezegen olsun. Elipsin tanımlamasına göre, PG+PF = 2a sabittir. AB = 2a elipsin büyük ekseni, OA = OB = a yarım büyük eksen ve CD = 2b küçük eksen, OC = OD = b yarım küçük eksendir. Odaklar arası uzunluğa FG = 2c diyecek olursak, 2c/2a = c/a = e oranı, elipsin şeklini belirleyen dış-merkezlik (eccentricity) parametresidir. Kolayca görüldüğü gibi, daire, dış-merkezliği sıfır olan elipsin özel halidir. Kopernik sisteminin önemli bir özeliği, gezegenlerin Güneş’e göreceli uzaklıklarını elde etme olanağını vermesi idi.
Örneğin, yörünge elipsinin yarım büyük ekseni (ki bu Yer-Güneş ortalama uzaklığına eşittir) birim olarak alınırsa, gezegenlerin Güneş’e göreceli ortalama uzaklıkları şöyle sıralanıyordu: Merkür (0,39); Venüs (0,72); Yer (1,00); Mars (1,52); Jüpiter (5,20); Satürn (9,55).
Sırası gelmişken hemen belirtelim ki, gezegen yörüngeleri şekillerde çizilirken, bizim de (Şekil 1’de) yapmış olduğumuz gibi elipslerin basıklıkları, daireden iyice ayırt edilebilsin diye, aşırı abartılmaktadır. Örneğin, Yerküre’nin yörüngesinin dış-merkezliği 0,017’dir. Büyük ekseni 10 santimetre olarak çizilen bir şekilde, elipsin büyük ekseni ile küçük ekseni arasındaki fark 0,014 milimetre olur. Böyle bir elips çizimini daireden ayırt etmek olanaksızdır. Kepler, sadece gezegen yörüngelerinin, bir odağında Güneş’in bulunduğu bir elips olduğunu kanıtlamakla kalmamış, önemli bir sonuç daha bulmuştu: gezegeni Güneş’e birleştiren (PG) doğru parçası, gezegen yörünge üzerinde dolanırken, eşit zamanlarda, eşit alanlar süpürür. Buna Kepler’in ikinci yasası (veya alanlar yasası) denmektedir. Ünlü Alman astronom, elde etmiş olduğu bu iki buluşu, 1609 yılında, Astronomia Nova (Yeni Astronomi) adlı kitabında yayınladı.
Güneş merkezli sistemin diğer önemli bir özelliği de, gezegenlerin Güneş çevresindeki sideral (yıldızsal) dolanım sürelerini sağlamasıdır. Yer’den gözlemlendiğinde, Güneş ile aynı doğrultuda görülen (yani ekliptikel boylamı Güneş’inkine eşit olan) gezegene, Güneş ile kavuşma konumunda (conjuction) denir.
Güneş’e, Yerküre’den daha yakın olan iç gezegenler için, biri Güneş ile Yerküre arasında, biri de Güneş’in ötesinde olmak üzere, iki kavuşma oluşur. Güneş’e Yerküre’den daha uzak olan dış gezegenler ise, hiçbir zaman Güneş ile Yer arasında olamayacaklarından, sadece Güneş ötesinde bir kavuşma olur. Buna karşılık, dış gezegenler için, karşı-konum (opposition) denen bir konum vardır: Güneş ile gezegen arasındaki ekliptikel boylam farkının 180 derece oluşu, diğer bir deyimle, Yerküre’nin Güneş ile söz konusu gezegen arasında bulunuşu.
Birbiri ardına gerçekleşen iki kavuşma-konumu veya iki karşı-konum arasında geçen süreye gezegenin sinodal dolanım süresi (periyodu) elenir. Yerküre de Güneş çevresinde dolandığından, sinodal dolanım süreleri, söz konusu gezegenin Yerküre’ye göre, göreceli dolanım süreleridir.
 Güneş’ten bakıldığı zaman, bir gezegenin bir yıldız ile art arda iki kavuşması (yani Güneş merkezli ekliptikel boylamlarının eşitlenmesi) arasında geçen süreye ise, gezegenin sideral (yıldızsal) dolanım süresi (periyodu) denir. Güneş merkezli Kopernik sistemi, gezegenlerin gözlemlenen sinodal dolanım sürelerinden, sideral dolanım sürelerinin, Yerküre’ninkine oranını elde etme olanağı vermektedir. Yerküre’nin Güneş çevresindeki sideral dolanım süresi birim olarak alınırsa, gezegenlerin göreceli dolanım süreleri şöyle sıralanır: Merkür (0,24); Venüs (0,62); Yer (1,00); Mars (1,88); Jüpiter (11,86); Satürn (29,46).
Güneş’ten bakıldığı zaman, bir gezegenin bir yıldız ile art arda iki kavuşması (yani Güneş merkezli ekliptikel boylamlarının eşitlenmesi) arasında geçen süreye ise, gezegenin sideral (yıldızsal) dolanım süresi (periyodu) denir. Güneş merkezli Kopernik sistemi, gezegenlerin gözlemlenen sinodal dolanım sürelerinden, sideral dolanım sürelerinin, Yerküre’ninkine oranını elde etme olanağı vermektedir. Yerküre’nin Güneş çevresindeki sideral dolanım süresi birim olarak alınırsa, gezegenlerin göreceli dolanım süreleri şöyle sıralanır: Merkür (0,24); Venüs (0,62); Yer (1,00); Mars (1,88); Jüpiter (11,86); Satürn (29,46).
Uzaklıklar ve dolanım süreleri (periyotlar) ile ilgili yukarıda verdiğimiz bu bilgilerden, Kepler çok ilginç bir sonuç çıkardı: zaman birimi olarak Yerküre’nin Güneş çevresindeki sideral dolanım süresi, uzunluk birimi olarak da, Yerküre-Güneş uzaklığının ortalaması (yörünge elipsinin yarı-büyük ekseni) alınırsa, bütün gezegenler için, dolanım sürelerinin kareleri, yörünge elipslerinin yarı-büyük eksenlerinin küplerine (3. kuvvet) eşittir. Sideral dolanım sürelerini T ve yarı-büyük ekseni a ile gösterirsek, bu sonucu T2 = a3 şeklinde yazabiliriz. Burada, kareler ile küplerin, orantılı olacak yerde, eşit çıkması, Yerküre’nin dolanım süresi ile Güneş’e uzaklığını birim almış olmamızdan ileri geliyor. Başka birimler ile ifade edilecek olursa, bu bağlantı genel olarak T2 = Ka3 şeklinde yazılabilir. K bütün gezegenler için aynı sabittir.
Kepler’in 3. yasası diye bilinen bu bağlantı, ilk ikisinden dokuz yıl sonra, 1618 de Harmonices Mundi (Dünyanın Uyumu) adlı kitapta yayınlandı.
Sözünü ettiğimiz Kepler’in bu üç ünlü yasası, gözlemlerle elde edilmiş olup, aralarında kuramsal bir bağ bulunmamakta idi. Gezegenlerin neden bu yasalara uyumlu olarak hareket ettiklerinin dinamikel nedeni, daha sonra, Isaac Newton tarafından açıklanacaktı.
Newton Çekim Yasası
Cambridge Üniversitesi’nin yetenekli matematik öğrencisi Isaac Newton, henüz yirmili yaşlarında iken, gök cisimlerinin hareketleri üzerinde düşünmeye başlamıştı. Rivayete göre bir elma ağacının altında oturmuş mehtabı seyrederken, önüne bir elma düştü. Düşen elma ile ay arasında hemen bir bağlantı kurdu. Acaba elmanın yere düşmesine neden olan yerçekiminin etkisi, Ay’a kadar uzanıyor mu?

Galileo Galilei, yatay düzlem üzerinde yapmış olduğu deneylerle, bir cismin hareket etmesi için, Aristotelesçilerin sandığı gibi, sürekli bir kuvvetin etkisi altında olması gerekmediğini, sürtünmeler gibi frenleyici bir etki olmadığı sürece, kazanılmış hareketin devam edeceğini gösterdi. Bu sonuç, şöyle ifade edilir: hareket halinde bir cisim, üzerinde hiçbir kuvvetin etkisi olmadığı sürece, kazanmış olduğu (sabit) hızla hareketine devam eder. Buna eylemsizlik ilkesi (principle of inertia) denir. Eğer Ay üzerinde hiçbir kuvvetin etkisi olmasa, yörünge üzerindeki A1 noktasından, yörünge teğeti A1 A2 boyunca kaçması gerekirken, A1 A3 yayı boyunca gitmesi, eylemsizlik ilkesine göre, onu düz yolundan saptıran, Yer’e doğru bir kuvvetin varlığını kanıtlamaktadır (Şekil 2). Bu kuvvet, yeryüzünde cisimlerin düşmesine neden olan ile aynı kuvvet olabilir mi? Gene Galilei’nin yeryüzünde düşen cisimler üzerinde yapmış olduğu deneylere göre, serbest bırakılan bir cisim, ilk saniyede (bugün kullandığımız birimlere göre) 490 santimetre düşmektedir. Eğer yerçekimi de, ışık şiddeti gibi, uzaklığın karesi ile ters orantılı olarak etkisini kaybediyorsa, o zaman Ay uzaklığında yerçekiminin şiddetinin, Yer-Ay uzaklığının karesi kadar zayıflaması gerekir. Newton döneminde Ay uzaklığının Yerküre yarıçapının 60 katı olduğu biliniyordu. Eğer bu varsayım doğru ise, Ay uzaklığında bir cismin ilk saniyesinde düşme miktarı 490/3600 = 0,136 santimetre olması gerekir. Uzaklık ve Yerküre çevresindeki dolanım süresi bilindiğinden, Ay’ın bir saniyedeki düşme miktarı olan A2 A3 basit bir hesapla bulunabilir.
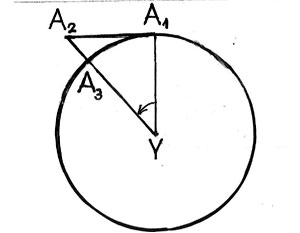
Newton bu hesabı yaptı ve varsayımının doğru olduğunu gördü. Yeryüzünde cisimlerin düşmesine neden olan çekim, uzaklığın karesi ile ters orantılı olarak, etkisini Ay’a kadar sürdürüyordu.
Gezegenlere uygulama
Bundan sonraki adım, Ay için geçerliliği kanıtlanan çekim yasasını, gezegenlere uygulamaktı. Genç Newton’un dehası burada bir kere daha kendini gösterdi. Kepler’in, içi metafiziko-mistik safsatalarla dolu olan kitaplarından, saman yığınından iğne bulup çıkartır gibi, kıymetli bilgiyi bulup çıkardı: Kepler’in gezegen hareketleri ile ilgili üç yasası. Gördük ki, gezegen yörüngeleri her ne kadar elips şeklinde ise de, dış-merkezlikleri (eccentricity) nispeten küçük olduğu için, ilk yaklaşım olarak, bir daire gibi ele alınabilir.

Newton da Ay yörüngesini dairesel varsayarak hesaplarını yapmıştı. Gezegenler için de, ilk yaklaşım olarak, aynı varsayım kabul edilebilir.
Hollandalı matematikçi C. Huygens, dairesel bir yörünge üzerinde harekette, merkezcil (centripedal) ivmenin daire çemberindeki hızın karesi ile orantılı ve daire yarıçapı ile ters orantılı olduğunu göstermişti. Yani hıza v ve yarıçapa r diyecek olursak, ivme= v2 /r dir. Diğer taraftan, bir F kuvvetinin etkisinde hareket eden bir m kütlesi için (Newton’un birinci hareket yasası diye bilinen) Kuvvet= (kütle)(ivme) bağlantısı geçerlidir. r yarıçaplı, gezegen yörüngesinin çemberinin uzunluğu 2πr, gezegenin çember üzerindeki v hızı ise (T sideral dolanım süresi olmak üzere) v=2πr/T dir.
Hızın bu değerini, dairesel hareketin merkezcil ivmesini veren v2 /r formülünde yerine koyarak ivme için
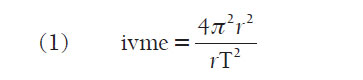
değerini ve (1) denkleminin pay ve paydasını r ile çarparak, nihayet,
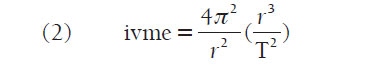
denklemini elde ederiz. Kepler’in 3. yasası gereği parantez içerisindeki (r3 /T2) sabit olduğundan, gezegenin ivmesinin uzaklığın karesi ile ters orantılı olduğu görülür.
Galileo Galilei düşen cisimler üzerinde yapmış olduğu deneyler ile, Aristotelesçilerin sandığı gibi, ağırlar daha hızlı, hafifler daha yavaş değil, bütün cisimlerin ağırlığı ne olursa olsun, aynı artan hızla (yani aynı ivme ile) düştüğünü göstermişti. Oysa, Newton’un birinci hareket yasası gereği, kuvvet = (kütle)(ivme) bağlantısına göre, farklı kütlelerdeki cisimlerin aynı ivmeyi kazanmaları için, onları harekete geçiren kuvvetin, kütle ile orantılı olması gerekmektedir. Böylece Newton, çekim kuvvetinin, kütleler ile düz orantılı, uzaklığın karesi ile ters orantılı olması gerektiği sonucuna vardı.
Newton hesaplarını yaparken, gök cisimlerinin bütün kütlelerinin merkezlerinde toplanmış noktasal kütleler olarak varsayılabileceğini sezgisel olarak varsaymıştı. Ancak bunun matematiksel olarak kanıt1anması gerekiyordu. Diğer taraftan, Kepler’in yasaları gereği, öngörmüş olduğu çekim yasasının geçerli olacağını göstermişti, bir de bunun “ters problemi”ni, yani çekim yasası gereği, Kepler yasalarının elde edildiğini göstermesi gerekiyordu.
O çağın matematiği, bu problemleri çözmek için yetersizdi. Kendisinin “flüksiyonlar metodu” dediği, bugün ise diferansiyel ve integral hesap dediğimiz, yeni bir matematiksel yöntem geliştirerek, karşılaştığı güçlüklerin üstesinden gelebildi, ve yirmili yaşlarında başlamış olduğu çalışmalarını, 20 yılı aşkın bir süre sonra, ancak 45 yaşına geldiğinde, Philosophiae Naturalis Principia Mathematica adlı ünlü eserinde, 1687 yılında yayımladı. Evrensel çekim, yasası dediği bu yasa, sözlü olarak şöyle ifade edilebilir: iki cisim birbirini kütleleri ile orantılı ve aralarındaki uzaklığın karesi ile ters orantılı olarak çeker. Matematiksel olarak ifade edersek, kütleleri m1 ve m2 ve aralarındaki uzaklık r olan iki cismin çekim kuvveti

‘dir.
G sabitine gravitasyon (çekim) sabiti denir ve sayısal değeri birim sistemine bağlıdır. Newton çekimi yasasından elde edilen hareket denkleminin çözüm eğrisi, integreasyon sabitinin aldığı değerlere göre, şu koni kesitlerinden birini verir:
e = 0 ise daire
0 < e < 1 ise elips
e = l ise parabol
e > l ise hiperbol
Bu eğrilere koni-kesiti veya kısaca konik denmesinin nedeni ise, bir koni yüzeyini, çeşitli açılarda kesen bir düzlem ile, koni yüzeyinin ara kesitinin, bu eğrileri verdiği, 2000 küsur yıl önce Pergeli Apollonios tarafından gösterilmiş olmasından kaynaklanmaktadır.
Newton’un elde etmiş olduğu ilginç bir sonuç daha vardı. Kepler’in üçüncü yasasının matematiksel ifadesinin doğru şekli,
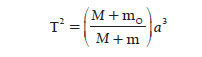
idi. Burada M Güneş’in kütlesi, m0 Yerküre’nin kütlesi ve m göz önüne alınan gezegenin kütlesidir. Ancak, gezegenlerin kütlesi en büyük olanı, Jüpiter’in bile kütlesi, Güneş’inkinin binde birinden küçük olduğu için, yasanın Kepler tarafından verilmiş olan şekli, çok iyi bir yaklaşımdır. Birinci sorunun yanıtını bir cümle ile özetleyecek olursak, gezegenlerin yörüngelerinin şeklini, Newton’un çekim yasası belirler diyebiliriz.
Soru 2- Kuyruklu yıldızlar, doğal ve yapay uyduların yörüngelerinin şekli nasıldır?
Newton’un uygulamak istediği bir alan da, kuyruklu yıldızların hareketi idi. Kuyruklu yıldızların da, gezegenler ile aynı çekim yasasına uyduklarına, ancak yörüngelerinin çok basık elipsler veya parabol, hiperbol gibi açık yörüngeler olduğunu düşünüyordu Newton. Yakın dostu Edmund Halley, bu varsayımı ilk uygulamaya koyan kişi oldu. Kasım 1682’de, Greenwich’de parlak bir kuyruklu yıldız gözlendi. Halley, bu kometin yörüngesinin hesabı için, Newton tarafından önerilen yöntemi uyguladı ve aynı kometin 1753 yılında tekrar geleceğini ilan etti. Ancak, 75 yıl sonra kendisinin bu olayı gözlemlemesinin olanaksızlığını bildiğinden öngörüsü doğru çıkarsa, bunun bir İngiliz tarafından yapılmış olduğunun anımsanmasını istedi.

Halley’in öngörüsünün gerçekleşmesine az bir süre kala, Fransız matematikçi Alexis Clairaut, söz konusu kuyruklu yıldızın yörüngesini yeniden ve daha geliştirilmiş matematiksel bir yöntem uygulayarak hesapladı ve kometin Güneş’e, en yakın durumu olan “perihel”den 1759 Nisan ayında geçeceğini, bir aylık bir belirsizlikle, açıkladı. Kuyruklu yıldız, 12 Mart 1759’da perihelden geçti. Bu geçiş, Newton kuramının büyük bir başarısı olarak kabul edildi ve adına Halley kometi denildi. Daha sonraki geçişleri de gözlenen bu komet, halk arasında en iyi tanınan kuyruklu yıldız oldu.
Uydulara gelince, zaten Newton ilk uygulamasını, doğal bir uydu olan Ay üzerinde gerçekleştirmişti. Yapay uydulara gelince, onların da genelde yörüngeleri elips şeklindedir. Ancak, uydunun kullanım amacına göre, yörüngenin dairesel olması da gerekebilir. Telekomünikasyon için gönderilen ve yeryüzeyinin hep aynı dikey doğrultusunda bulunması istenen (geostationary) uydular, dairesel yörüngeler üzerinde bulunurlar. Bir uyduyu yeryüzeyinden 35.727 km (veya Yer merkezinden 42.092 km) uzağa gönderir ve Yer merkezi ile uydu arasındaki doğrultuya dik olacak şekilde, o yükseklik için gereken hızı verirseniz, uydunun yörüngesi dairesel olur. Bu durumda uydu, Yer çevresince, Yer’in dönüş yönünde ve açısal dönüş hızına eşit hızla döner ve sürekli olarak yeryüzeyinin aynı bölgesi üzerinde durur.
Bu sorunun yanıtını da bir cümle ile özetleyecek olursak, diyebiliriz ki, bütün kapalı yörüngeler (periyodik) genelde elips veya elipsin özel hali olan daire şeklindedir. Kapalı (periyodik) yörüngelerin çoğunluğunun elips olmasına gelince, dış-merkezlik (eccentricity) denilen büyüklüğün sıfır ile bir arasındaki sonsuz sayıdaki değerlerden birini alma olasılığı, e = 0, e = 1 gibi özel değerler alma olasılığından daha büyüktür.
Soru 3- Gökcisimlerinin yörüngelerinin şekilleri arasındaki farkların kaynağı nedir?

Birinci sorunun yanıtında gördük ki, yörüngeler, konik denilen (elips, parabol, hiperbol) eğrilerden oluşur. Bu eğrilerden hangisinin olacağı ise, göz önüne alınan cismin hızına bağlıdır. Parabolik hız diye tanımlanan bir hız vardır. Eğer söz konusu cismin hızı bu değerden küçük ise, yörünge bir elips (veya özel halde daire) olur. Tam bu hıza eşit ise parabol, bu hızdan büyük ise hiperbol olur. Gezegen, uydu (doğal veya yapay) gibi kapalı yörünge üzerindeki periyodik hareketlerde, yörünge eğrisi, ancak elips (özel olarak daire) olabilir. Parabolik hıza eşit veya bu hızdan büyük hızlara sahip olan gök cisimleri ise, açık bir yörünge üzerinde olduklarından, matematiksel olarak ifade edecek olursak, sonsuzdan gelir, çekim merkezi çevresinde bir defa dolanır ve tekrar gelmemek üzere, sonsuz uzağa giderler. Her ne kadar, kuyruklu yıldızların çoğunluğu basık eliptikel yörüngeler üzerinde iseler de, bazılarının parabolik yörünge üzerinde olmaları olasılığı da vardır.
Newton kuramı üzerindeki tartışmalar
1687 yılında Newton’un başyapıtı Principia yayınlanır yayınlanmaz, karşı çıkanların da sesi yükselmeye başladı. Huygens, Newton’un yapmış olduğu hesapların doğru olduğunu kabul ediyor, ancak birbirinden bu kadar çok uzak gökcisimlerinin, aralarında hiçbir temas olmadan, uzay boşluğunda bir kuvvetin etkisinde olabileceğine inanmıyordu. Leibniz de, Principia’yı okuduktan sonra, Huygens’e göndermiş olduğu bir mektupta aynı eleştirileri dile getirmişti. Her ikisi de, Newton’un, çekim kuvveti diye ileri sürdüğünün açıklanması gereken gizemli bir şey olduğunda birleşiyorlardı.
Newton da Principia’yı yayınlarken, bu gibi eleştirilerle karşılaşacağını öngörmüştü ki, çekim yasasından söz ederken, nedeni hakkında “bir varsaym ileri sürmüyorum” demiş ve “sanki her şey, kütlelerle orantılı ve uzaklıkların karesi ile ters orantılı bir kuvvet varmış gibi oluşuyor” diye eklemişti. Huygens ve Leibniz’in başlatmış oldukları tartışmalar, biliminsanları arasında yıllarca sürecek, ancak kuramın uygulamalardaki büyük başarısından sonra, güncelliğini kaybederek, küllenmeye yüz tutacaktır, ta ki… Albert Einstein adında bir gencin bu konuya ilgi duymasına kadar.
Hemen hemen bütün ömrünü elektrik ve magnetik olayları incelemeye adamış olan ünlü İngiliz bilgin Michael Faraday, deneylerini açıklamak için yeni bir kavram geliştirmişti: “kuvvet çizgileri” ve bu çizgilerin oluşturduğu “kuvvet alanı”. Somut olarak bunu göstermek için de, ilginç bir deney gerçekleştiriyordu: bir mıknatısın üzerine örtülen kâğıda demir kırıntıları dökmek. Demir tanecikleri hemen kendiliğinden mıknatısın bir kutbundan ötekine doğru giden yollar boyunca dizilerek, ilginç bir görüntü oluşturuyordu. Faraday bunlara “kuvvet çizgileri” ve tümünün oluşturduğu görüntüye de “kuvvet alanı” diyordu. Faraday’ın bir öğrencisi olan James Clerk Maxwell, bu kavramlardan hareket ederek, elektromagnetik alan teorisinin genel denklemlerini oluşturdu. “Newton zamanından beri fizikteki en önemli gelişme” dediği Maxwell kuramına, Albert Einstein, öğrencilik yıllarından beri büyük bir hayranlık duymakta idi. Maxwell kuramına göre, elektromagnetik etkileşim, belirli sabit bir hızla yayılıyordu, ve bu hız da ışık hızına eşitti. Oysa iki cisim arasındaki çekim kuvvetini belirleyen Newton denklemine göre, bu kuvvet, sadece iki cisim arasındaki uzaklığa ve kütlelere bağlı idi: zaman, dolayısıyla etkileşimin yayılma hızı, Maxwell kuramında olduğu gibi denklemin içerisinde yer alıyordu.
İki cisim arasındaki çekim kuvveti birinden ötekine anında geçiyordu. Bu ise, etkileşimin, sonsuz bir hızla yayıldığı anlamına geliyordu. Newton yasasına, Principia’nın yayınından beri yapılan eleştiri de buydu.
Euklides geometrisinde yüzeyler için kullanılan “yüzeyin eğriliği” kavramını, Alman matematikçi Bernhard Riemann, üç boyutlu uzaya genelleştirerek, yeni bir geometri türü geliştirmişti. Einstein bu kavramı Genel Görelilik Kuramında kullanarak, Newton’un “çekim kuvveti” diye algıladığı şeyin, maddenin çevresindeki uzayı eğip bükmesinden yani üç boyutlu uzayı “eğriltmesinden” kaynaklandığını varsaydı. Riemann geometrisini kullanarak geliştirdiği Genel Görelilik Kuramının denklemlerine göre, kütle çevresinde belirli bir hızla yayılan bir “eğrilik alanı” oluşturuyor ve nasıl ki viraja giren tren, eğik rayların yönlendirmesi ile doğru yolundan sapıyorsa, uzayı eğen kütle de, çevresinden geçen cisimlerin yollarından sapmalarına neden oluyordu.(1) Rayları görmeyen birisi, trenin doğru yolundan sapmasını, virajdaki eğik rayların geometrik eğrilik merkezinde, sanki bir çekim kuvveti varmış gibi algılayabilir. Zaten Newton da sezmiş olmalı ki “her şey sanki bir çekim kuvveti varmış gibi oluşuyor” diye bunu belirtmişti. Eğilen uzayın görünen etkisi, sanki bir çekim kuvvetinden kaynaklanıyormuş gibi belirdiğinden, bugün de “çekim kuvveti” ve “çekim alanı” gibi deyimleri hâlâ kullanmaya devam ediyoruz. Böylece, uzun süreden beri tartışma konusu olan, hiçbir temas olmadan uzaktan etkileşen kuvvet kavramı terk edilmiş oldu.
Ancak, Genel Görelilik Kuramı, her ne kadar temel bir kavram değişikliği getirmiş ise de Newton teorisi ile arasındaki ayrılık, ancak ışık hızına yakın “relativist hızlar” ve güçlü çekim alanlarında etkisini gösterir. Küçük hızlar ve zayıf çekim alanlarında, her iki teorinin verdiği sonuç arasındaki fark, gözlem ve deney verilerinin duyarlılık sınırlarının altında kalır.
Bugün, gerek gök mekaniğinde (Güneş’in çekim alanına en yakın ve en hızlı hareket eden Merkür gezegeninin yörüngesindeki ufak bir uyumsuzluk hariç) gerekse yeryüzündeki en hızlı araçları ilgilendiren problemlerde, (uzaya gönderilen araçların yörünge hesaplarının bir kısmi dahil) hâlâ klasik Newton mekaniği geçerliliğini korumakta ve uygulanmaktadır.
İki yüz küsur yıldan beri, en seçkin matematikçilerin özenle geliştirmiş oldukları bu görkemli kuramın denklemleri, ünlü Fransız matematikçi Henri Poincaré’nin deyimi ile “daha kullanışlı”dır. Bundan dolayı, okulların ve üniversitelerin programlarının başköşesinde saygın yerini korumaktadır.
Dipnot
1) Genel Görelilik Kuramının öngördüğü çekim dalgalarının (gravitational waves) deneysel olarak saptanması, bugün astronominin güncel konularından biridir.