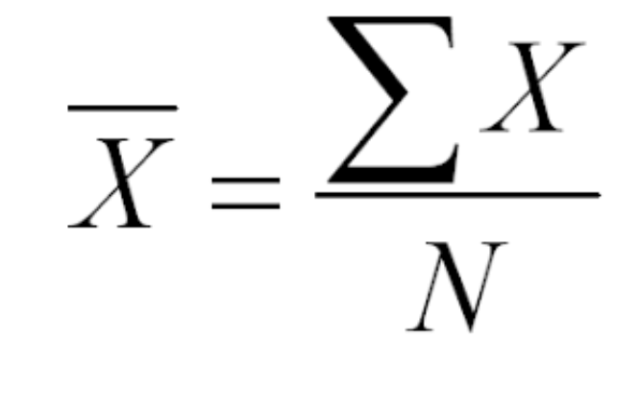Tülin Acar Otbiçer
Ortalama, çoğu kişi için dört işlem bilgisi gerektiren bir denklemdir. Ancak ortalama kavramını açıklamak, hesaplamak kadar kolay değildir. Çünkü salt matematiksel bir işlemden ziyade ortalama kavramının çok daha farklı belirlenimleri söz konusudur. Ortalama;
– Bir orta nokta mıdır?
– Ne çok ne de az olan bir denge seviyesi midir?
– Sıklık bakımından en çok gözlenen midir?
– Kabaca tahmin edilen bir ölçü müdür?
– İki şeyin arasında olan mıdır?
Ortalama kavramının tarihsel köklerine indiğimizde ilkin İskenderiyeli Öklid ve onun Elemanlar isimli eseriyle karşılaşmaktayız. Çünkü Öklid’in Elemanlar eserinde orta değer, orta orantı (geometrik ortalama) üzerine önermeler bulunmaktadır. Diğer taraftan Antik Yunan filozofu Aristoteles Nikomakhos Etik isimli eserinde erdemlerin yapısı üzerinden bir kavram olarak ortalamanın, ortanın felsefesini yapmıştır ve “bize göre ortalama” ile “matematiksel ortalama” üzerine ayrımda bulunmuştur.
Diğer taraftan aritmetik, geometrik ve harmonik ortalama söylemleri arasındaki ayrımları düşünmek oldukça yararlıdır. Çünkü aritmetik ortalama ile harmonik ya da geometrik ortalama aynı şey değildir. Bugün yaygın olarak “average” sözcüğüyle kastedilen ölçümlerin aritmetik ortalamasıdır. Türkçeye çevirisi ortalama olarak yapılan “mean” ile “average” olan İngilizce sözcüklerinin tarihte aynı anlamı ifade etmediğini görürüz. Bugün her ne kadar mean ile average sözcükleri eş anlamlı olarak kullanılsa da işin aslı öyle değildir. Dilsel köklere indiğimizde İngilizce “mean” sözcüğü middle (orta) ve istatistiksel bir terim olan median (ortanca) terimlerinden türemiştir. Middle sözcüğünün kökü ise Latinceden “medium” sözcüğüne dayanmaktadır. “Average” sözcüğünün ise 1558’li yıllarda İngiltere’de I. Elizabeth zamanında “gemiyle taşınan malların hasar görmesi sonucunda alıcı ve satıcı arasında gider veya zararın eşit dağılımını” ifade etmek amacıyla kullanıldığını görmekteyiz. Dolayısıyla 15. yüzyıllarda “ortalama” kavramı, bir tür eşitsizlik problemine işaret etmektedir. Tam bu noktada şunu söylemek yanlış olmayacaktır: Doğada birbirine eşit olmayan ölçümler pekâlâ vardır, ancak bu eşitsizlikleri eşit kılmanın bir yolu, aritmetik ortalamadır!
– Türkiye’de beklenen yaşam süresi, 78 yıldır.
– 2019 yılı insani gelişim raporuna göre 25 yaş ve üzerindeki bireylerin ortalama eğitim süresi 8 yıldır.
– Türkiye İstatistik Kurumu’nun yaptığı araştırmaya göre günde 6 saat televizyon izliyoruz, 3 saat internete giriyoruz ancak kitap okumaya sadece 1 dakika ayırıyoruz.
– Dünyada kişi başına yapılan kitap harcaması 1,3 dolar, Türkiye’de ise çeyrek dolardır (25 sent).
– 15 yaş ve üzerindeki bireylerin kültür ve eğlence amacıyla müzik ve sahne sanatları faaliyetlerine bir ayda ayrılan ortalama süre 25 dakikadır.
– IMF raporuna göre 2017 yılında gelişmekte olan ülkelerin milli geliri 11 bin 760 dolardır.
Bu ifadelerin benzerlerini zaman zaman TV haberlerinde duyuyoruz ya da sosyal medyanın kaynaklarında okuyoruzdur. Yukarıdaki ifadelerin her biri bize -açıkça ifade edilmemiş olsa bile- “ortalama” kavramına ilişkin bir bilgi sağlamaktadır. Bu bilgi kimi zaman yaklaşık olarak beklenen bir değeri, kimi zaman sıklıkların en fazlasını, kimi zaman da merkezi bir yığılım noktasını ifade etmektedir.
Bir ölçüm kümesindeki nicel ölçümlerin toplanıp, toplamın ölçüm sayısına bölünmesi sonucunda elde edilen değere “aritmetik ortalama” denir.
Aritmetik ortalama, tanımı gereği ölçme sonuçlarının toplamını gerektirdiği için en az iki ölçme sonucu olmak durumundadır. Dahası toplama işleminin, nicel ölçme sonuçları üzerinde yapıldığında anlamlı olduğu unutulmamalıdır. Sınıflama ya da sıralama düzeyindeki kategorik ölçümler için “aritmetik ortalama” istatistiğinin hesaplanması, özü gereği bir anlam ifade etmemektedir. Örneğin ölçülen nitelik cinsiyet olsun. Kız ve erkek olan ölçme sonuçları, kategorik sınıflama düzeyindedir. 15 kız öğrenci ile 25 erkek öğrencinin ortalaması cebirsel bir işlem olarak (15+25)/2=20 eder. Ancak bu ölçüm kümesinin ortalaması ya 20 kız ya da 20 erkek öğrencidir söylemi, işin özü gereği doğru olmayacaktır. Aritmetik ortalamanın tanımına dikkat edilirse, aritmetik ortalama doğrudan bir ölçme sonucu değildir, ölçüm kümesindeki tüm ölçümlerden elde edilen noktasal bir değerdir.
X üzerinde yatay çizgi olan bu sembol ( ) aritmetik ortalama işleminin kabul görmüş istatistiksel gösterimidir. Aritmetik ortalamanın elde ediliş işlemini şu şekilde sembolize ederiz:
![]()
X sembolü, ölçüm kümesindeki ölçme sonuçlarının her birini ifade etmektedir. N, ölçüm sayısının sembolik gösterimidir. ∑ simgesi ise veri setindeki ölçümlerin toplanacağının ifadesidir.
∑, , X, N, = ve / olmak üzere toplam 6 adet sembol bize şunu söyler: Aritmetik ortalama, ölçme sonuçlarının toplamının, toplanan ölçüm sayısına bölünmesi işlemine eşittir.
Boşluksuz 92 karakterden ya da 11 sözcük ve 1 cümleden oluşan bir dili, tasarruf yaparak 6 karakterli bir dile indirgemiş olduk. Bir başka deyişle, 92 karakterle ifade edilen bir düşünceyi 6 karakterle ifade edilen bir düşünce sistemine eşdeğer de tutmuş olduk. Yani, gündelik bir dili, matematiğin diliyle ifade etmiş olduk. Matematik bir düşünce sistemidir. Her düşünce sisteminin de bir dili vardır. Şimdi aritmetik ortalama işleminin elde edilişine bir örnek verelim.
6 bireyin boy uzunlukları 170, 164, 178, 162, 174 ve 158 cm olarak ölçülmüş olsun. Bu ölçme sonuçları toplanıp, toplam değer ölçüm sayısına bölünürse “aritmetik ortalama değeri” elde edilmiş olacaktır. Aritmetik ortalamanın hesaplanması, bir tür toplama ve bölme işlemi yapabilme bilgisidir.
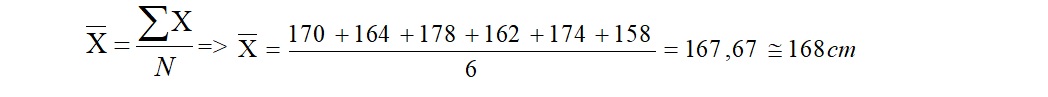
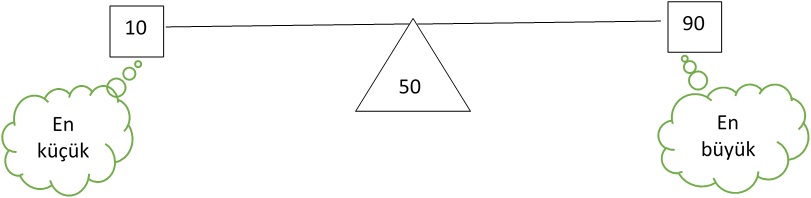
Örneğin, farklı uzunluklardaki iplerin her birinin yaklaşık olarak tam ortasının bulunması, özünde orta değerin bulunmasıdır. Fakat başka bir açıdan da aritmetik ortalama işlemidir. Ölçümlerin uç (en düşük ve en yüksek) değerlerinin bilinmesi durumunda, öteki ölçümleri hiç bilmesek de, hiç ölçmeksek de ölçümlerin orta değerini aritmetik ortalama işleminden yararlanarak elde ederiz. Bunun adı, beklenen aritmetik ortalamadır. Örneğin 10 ile 90 puan arasında değişen puanların orta noktası, bir başka deyişle orta değeri, 50 puandır. Yani 50 puan, hem 10 hem de 90 puanına eşit uzaklıkta bulunan bir orta noktadır. Bu örnekten şu çıkarımı rahatlıkla yapmak mümkündür, en düşük ve en yüksek ölçümlerden veya uç değerlerden elde edilen aritmetik ortalama, aynı zamanda hem beklenen aritmetik ortalama hem de orta değeridir.
Pratikte ölçme sonuçlarının aritmetik ortalaması, bir değer olarak, en küçük ve en büyük ölçme sonuçları arasında bir değerde olmak zorundadır. Bir başka deyişle, aritmetik ortalama en küçük ölçme sonucundan daha küçük; en yüksek ölçme sonucundan da daha büyük olamaz.
Nicel ölçümlerin bulunduğu bir ölçüm kümesinde, ölçümlerin uç değerlerinden ortanca ve tepe değer istatistiği etkilenmez. Ancak, aritmetik ortalama, uçlardaki ölçümlerin değerlerinden bilhassa en çok etkilenen bir istatistiktir. Nasıl yani? Anlamak için aşağıda verilen ölçümlerin tepe değerini, ortancasını ve ortalamasını hesaplayalım.
| Birey no | Ölçme sonucu (kg) |
| 001 | 55 |
| 002 | 60 |
| 003 | 60 |
| 004 | 60 |
| 005 | 65 |
| 006 | 72 |
| 007 | 72 |
| 008 | 75 |
| 009 | 155 |
9 bireyin kütlelerine ilişkin ölçümlerin tepe değeri 60 kg; ortanca değeri 65 kg, aritmetik ortalaması 74,89 kg’dır. Veri setinin uçlarındaki değerler 55 kg ve 155 kg’dır. Fakat 155 kg aynı zamanda aşırı uç bir değerdir ve aritmetik ortalamayı kendine doğru çekmektedir. Bu ölçümler, 25 yaşındaki sporcular üzerinde elde edildiği için 155 kg gibi bir ölçme sonucu beklenen kütle normunun üstündedir. 155 kg olan uç değerin, 60 olması durumunda ölçümlerin aritmetik ortalaması 64,33 kg olacaktır. Bu örnekte, 155 kg ölçümünün olması aritmetik ortalamayı 155’e doğru çekmiştir. Dolayısıyla bir veri setinde aşırı uç değerin mevcudiyeti dikkatle incelenmeli, araştırma nesnesine, ölçüm sayısına ve ölçümün niteliğine bağlı olarak değerlendirilmelidir. Aşırı uç değer(ler), veri setinden ayıklandıktan sonra aritmetik ortalama istatistiği hesaplanmalıdır dense de bunun adı, gerçeği çarpıtmaktır. Burada önemsenmesi gereken öncelikli husus uç değerin gerçeği yansıtıp yansıtmadığıdır. Örneğin 7-10 yaş arasındaki çocukların boy uzunlukları ölçülmüş olsun ve boy uzunlukları 109 ile 172 cm arasında değişkenlik göstermiş olsun. Ölçüm ile ölçülenin mutabakatı var mı yok mu sorgulanmalıdır. 7-10 yaş grubunda 109 cm ve 172 cm ölçümleri, ölçümlerin iki uç değeridir. Peki, bu uç değerler, aşırı uç değer midir? Karar vermek için önce bu uç değerlerin, gerçeğin bir parçası olup olmadığı araştırılmalıdır. 7-10 yaş grubundaki çocukların boy uzunluğu normu 109-150 cm arasında değişkenlik gösterdiği bilgisine dayanarak ölçüm setindeki 172 cm aşırı bir uç değerdir ve gerçeği yansıtmamaktadır. İşte bir uç değerin gerçeği yansıtmaması durumunda ölçümün ölçüm setinden çıkarılması uygundur.
Örneğin 10 kişiden oluşan bir arkadaş grubunun aylık kazançları TL cinsinden tabloda gösterilmiş olsun. Bu gruptaki kişilerin kazançları 2340 TL ile 25000 TL arasında değişkenlik göstermektedir. Bir bakıma ölçümlerin hipotetik uç değerleri 2340 TL ve 25000 TL’dir. Ölçümlerin aritmetik ortalaması, [(2340+2340+2340+2500+2340+2340+2340+2340+2340+25000)/10]= 4622 TL’dir.
| Kişi no | Gelir (TL) |
Bu durumda bu arkadaş grubunun ortalama aylık kazancı, 4622 TL’dir. Bir bakıma 10 kişinin her biri için aylık kazanç 4122 TL’ye eşitlenmiş oldu. Bireylerin aylık kazançlarına tablodan bakınız. 9 kişinin aylık kazancı birbirlerine çok benzer değil mi? Ancak 25000 TL diğerlerinden oldukça ayrık. Bu ölçümü, uç değer olarak atfedip ölçüm setinden çıkarıp aritmetik ortalama hesaplandığında gerçeği yamultmaya başladık demektir. İlkin, 10 kişilik arkadaş grubu, 9 kişiye indirgenmiş oldu. 9 kişinin kazanç ortalaması 2358 TL’dir. |
| 1 | 2340 | |
| 2 | 2340 | |
| 3 | 2340 | |
| 4 | 2500 | |
| 5 | 2340 | |
| 6 | 2340 | |
| 7 | 2340 | |
| 8 | 2340 | |
| 9 | 2340 | |
| 10 | 25000 |
Peki, başlangıçta ilan ettiğimiz 10 kişiden oluşan arkadaş grubunun aylık kazanç ortalaması 2358 TL denebilir mi? Hayır. Dahası bazı meslek grupları için 25000 TL’lik aylık kazanç olağandır ve kazanç normunun dışında değildir. Misal 25000 TL’lik kazanca sahip kişi, bir doktor olabilir. Ölçümlerin birbirine daha çok benzeştiği küçük fakat gerçeklikle bağı bulunan uç değerli örneklemlerde, uç değerler budanmamalıdır. Peki, ne yapılabilir? Bu ölçüm kümesi için tepe değer ve ortanca istatistiği, aritmetik ortalamaya nispetle bilgi verme gücü daha yüksektir. Bu 10 kişilik arkadaş grubunun kazanç ortancası, 2340 TL’dir. Ölçümlerin tepe değeri 2340 TL’dir. Bir başka deyişle kişilerin %80’inin (8’inin) aylık kazancı, 2340 TL’dir. Buna mukabil, bu arkadaş grubunun kazanç ortalaması 4622 TL’dir. Ortanca değer ile aritmetik ortalama arasındaki fark 2282 TL’dir. Aritmetik ortalamaya göre gerçekte 9 kişinin aylık kazancını, 2282 TL artırılırken gruptaki bir kişinin aylık kazancını da 20378 TL azaltmış olduk. Böylece eşit olmayan ölçümleri eşit kılmış olduk.
Sonuç olarak aritmetik ortalama, ölçümlerin toplamının ölçüm sayısına bölünmesiyle elde edilen bir değer olsa da kavramın ne’liğini tam olarak yansıtmayabilir. Kavramın tarihsel kökleri Antik Yunan’a kadar uzanıyor olması “ortalamanın” sadece bir “orta nokta” olmanın ötesinde, denge, sıklık ve tahmin gibi farklı belirlenimleri bulunmaktadır. Özellikle bir ölçüm kümesinde aşırı uç değerlerin varlığında aritmetik ortalamanın gerçekliği çarpıttığı göz ardı edilmemeli ve ortanca ve tepe değer gibi diğer istatistikler bize daha doğru bir resim sunabilir.
Not: Acar Otbiçer, Tülin (2024). Kavramları, İlkeleri ve Uygulamalarıyla Ölçme ve Değerlendirme isimli kitaptan alıntılanmıştır.