Escher “Gerçek bilimlerde hem öğretim hem bilgi olarak cahil olsam da, meslektaşım sanatçılara kıyasla matematikçilerle daha çok ortak noktam bulunuyor” demişti. Bir öğrenci olarak matematikle çatışmış olsa da, bir grafik sanatçısı olduğunda matematiksel araştırma yürütmeye, yeni geometrik fikirler öğrenmeye, matematiksel kavramları tasvir etmeye ve matematikle ilgili sorular sormaya itilmişti. Çalışmalarının bilim topluluğu için yarattığı etkinin ölçeğini tahmin bile edemezdi.
Yazar: Doris Schattschneider
Bethlehem/Pennsylvania’daki Moravian College’de matematik profesörü
Hollandalı grafik sanatçısı M. C. Escher’in matematiksel yönü genellikle kabul edilmiş olmakla birlikte, az sayıda hayranı, çalışmalarındaki matematiksel derinliğin farkındadır. Muhtemelen Rönesans’tan bu yana ilk kez bir sanatçı matematiğe, sadece matematiksel fikirleri sanatına uygulamak adına, Escher’in odaklandığı genişlikte odaklanmıştır. Matematiği (özellikle geometriyi) birçok resim ve baskısını yaratırken kullanmıştır. Birçok çalışmasını matematiğe borçludur. Çok sayıda çalışması soyut matematiksel kavramların görsel metaforlarını ortaya koyar. Escher, özellikle sonsuzluğu tasvir etme konusunda saplantılıdır. Çalışmaları biliminsanları ve matematikçilerin çalışmaları için kıvılcım niteliğinde olmuştur. Ancak en ilginci, Escher, yıllar boyunca bazıları daha sonraki keşiflere önayak olan, kendi matematiksel araştırmalarını yürütmüştür.
Ancak bütün bunlara rağmen Escher matematiği anlamak veya üretebilmekle ilgili herhangi bir yeteneğe sahip olduğunu kararlılıkla reddetmiştir. Oğlu George, bunu şöyle açıklamıştı:
“Babam aklının çalışma biçiminin bir matematikçiye yakın olduğunu idrak etmekte zorlanırdı. Çalışmalarına, resimlerinde konuştuğu ortak dili anlamaya hazır olan matematikçilerin ve biliminsanlarının ilgi duymasından büyük keyif alırdı. Maalesef matematiğin özelleşmiş dili, matematikçilerin de onun uğraştığı kavramlarla uğraştığı gerçeğini ondan sakladı. Biliminsanları, matematikçiler ve M. C. Escher bazı çalışmalarına aynı şekilde yaklaşıyorlar. Soyut bir dünyada izin verilen olayları tanımlayan olası kurallar kümesini ilham ve tecrübe ile seçiyorlar. Daha sonra bu kuralları uygulamanın sonuçlarını daha ayrıntılı keşfetmek adına devam ediyorlar. Kurallar iyi seçilmişlerse, heyecan verici keşiflere, teorik gelişmelere ve tatmin edici çalışmalara yol açıyorlar.”(1)
Escher’in zihninde matematik, okulda karşılaştıklarıydı: Semboller, formüller ve problemleri çözmek için uygulanması gereken tarif edilmiş teknikler. Kendi sorularını formüle etmek ve bunlara kendi tarzında yanıtlar aramak ona matematik yapmakmış gibi görünmüyordu.

1937’ye kadar
M. C. Escher Arnhem/Hollanda’da 4 erkek kardeşin en küçüğü olarak büyüdü. Babası inşaat mühendisiydi ve diğer 3 kardeşinin tamamı biliminsanı oldu. Evdeki atmosfer ona, daha sonraki çalışmalarını karakterize edecek olan sabırlı metodik yaklaşımı da içeren bilimsel araştırmanın alışkanlıklarını aşılamış olabilir. Ayrıca genç adamlara, daha sonra Escher için tahta baskılarda çok faydalı olacak marangozluk teknikleriyle ilgili düzenli dersler veriliyordu.
Okul hayatı ev hayatından daha faydasız olmalıydı. Okul yıllarını hatırladığında Escher, bir seferinde “Aritmetik ve cebirde inanılmaz zayıf bir öğrenciydim ve hâlâ figürler ve harflerin soyutlanmasında büyük zorluk yaşarım. Katı geometrisinde, hayal gücüme cazip geldiği için bir parça daha başarılıydım ama o konuda bile okulda üstün bir durumda değildim” demişti.(2) Yine de resimde iyiydi ve lise resim öğretmeni linolyum baskı yapması için onu cesaretlendirdi.
1919’da Escher, Haarlem Mimarlık ve Süsleme Sanatları Okulu’na mimarlık okuma niyetiyle girdi, ama resim ve grafik sanatları öğretmeni Samuel Jessurun de Mesquita’nın tavsiyesi ve ailesinin izniyle kısa süre sonra grafik sanatlar bölümüne geçti. Haarlem’deki çalışmalarından üçü düzlemlerin doldurulması şeklindeydi: İki tanesi eşkenar dörtgenlerin doldurulması temelliydi, diğeri de dördü baş aşağı olmak üzere sekiz seçkin baş figürüyle doldurulmuş bir dikdörtgendi. Düzlemin doldurulması kısa süre sonra bir saplantı haline dönüşecekti.

baskı çalışması.
Haarlem’i 1922’de bitirdikten sonra İtalya ve İspanya’da neredeyse bir yıl seyahat etti ve portfolyosunu manzara taslaklarıyla, binaların ayrıntılarıyla ve doğadaki bitkiler ve küçük canlıların kılı kırk yaran çizimleriyle doldurdu. Bu gezi esnasında Granada/İspanya’daki El Hamra Sarayı’nı ziyaret etti ve özellikle “büyük karmaşıklığı ve geometrik sanatsallığı” nedeniyle ilgisini çeken bir bölümünün taslağını çizdiği mayolika karo süslemelerinin (Endülüs çinilerinin) zenginliği karşısında büyülendi. El Hamra’nın çinileriyle bu ilk karşılaşması, kendi çinilerini yapma konusundaki ilgisini artırdı. Her şekilde, 1920’lerin ortalarında, bazıları ipek üzerine elle çizilen, tek şekle sahip birkaç “mozaik” üretti. Her zaman geometrik şekillere sahip olan Mağrıbi çinilerin aksine (kendisinin “motif” olarak adlandırdığı) Escher’in çini şekilleri ana hatlarıyla canlı yaratıklar olarak tanınabilir olmalıydı. Bu erken denemeler, uyumu koruyarak, öteleme, yarım dönme (180 derece dönüşler), yansıma ve ötelemeli yansıma gibi basit dönüşümleri en azından sezgisel olarak nasıl yapabileceğini bildiğini gösterir.
Escher 1924’te evlendi ve çift, iki oğlan çocuklarının doğacağı Roma’ya yerleştiler. 1935’e kadar sık sık, çoğunlukla güney İtalya’ya taslak gezileri düzenledi ve daha sonra Roma’daki stüdyosuna dönerek bunları taş ve ahşap baskılarında kullandı. 1935’de İtalya’da faşizmin yükselişiyle ve oğullarının hastalıkları nedeniyle, ailesini İtalya’dan İsviçre’ye taşıdı. 1936’da uzun bir deniz yolculuğuna çıktı ve bu yolculuk sırasında eşi Jetta’nın da katılımıyla El Hamra’da üç gün geçirdi. Bu ikinci El Hamra ziyareti, İtalya’dan ayrılış dekoruyla birleşince, çalışmasında büyük bir dönüşüme neden oldu: Doğa manzaraları yerini fikir manzaralarına bıraktı.(3) Bundan sonra artık taslak ve baskıları, dağlık köylerde, doğada ve mimaride bulduklarından ilham almayacaktı. Artık fikirleri ancak zihninin girintilerinden bulunabilirdi.

Escher bu El Hamra ziyaretinden sonra “hayvan şekilleriyle bulmaca çözmek adına zamanımın önemli bir parçasını harcadım” diye yazmıştır. El Hamra taslaklarını ve çinilerin birbirleriyle olan geometrik ilişkilerini inceleyerek birbirleriyle bağlantılı motiflerden oluşan bir düzine yeni simetri çizimleri yapabilmişti.(4) Bunlardan biri, birbirine bağlı Çinli çocukları gösteriyordu. 1937 ilkbaharında figürlerin metamorfozunu yaratmak adına düzlem doldurmayı ilk kez biraz da olsa kullandığı çalışmasını yaptı. Metamorphosis I’de Atrani kıyı kasabasının binaları sırasıyla küplere ve sonrasında Çinli çocuklara dönüşüyordu. Çalışma bir hayal ürünüydü, yeni oluşan düzlem doldurma ilgisini Amalfi kıyılarına olan sevgisiyle birleştiriyordu ama Escher bu çalışmasını hiçbir zaman sevmedi çünkü bir öyküsü yoktu; Çinli çocuklarla bir İtalyan kentini nasıl birbirine bağlayabilirsin ki?
1937 Temmuz’unda Escher ailesi, üçüncü oğullarının doğacağı bir Brüksel banliyösüne taşındı. O yılın Ekim ayında Escher fakir simetri portfolyosunu, kristalografların ilgisini çekebileceğini düşündüğü jeoloji profesörü büyük ağbisi Beer’a gösterdi. Beer, Escher’e faydalı olabileceğini düşündüğü bazı teknik araştırmaların listesini gönderdi. Beer’ın listesinde, tamamı Zeitschrift für Kristallographie’den olmak üzere, 1911 ile 1933 arasında F. Haag, G. Polya, P. Niggli, F. Laves ve H. Heesch tarafından yazılmış 10 makale vardı. Escher sadece Haag ve Polya’nın makalelerini faydalı buldu.
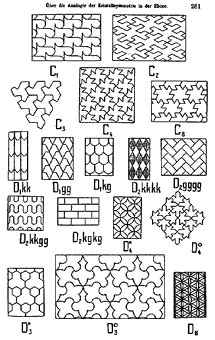
tablosunun, Polya tarafından imzalanmış bir kopyası.
Haag’ın makalesi, Escher’in “düzenli” düzlem doldurması için berrak bir tanım ve bazı tasvirler sağlıyordu. Defterlerinden birine Escher, Haag’ın “düzlemin düzenli bölünmesi” üzerine tanımını dikkatle not etmişti:
“Düzlemin düzenli bölünmesi bir araya gelmiş benzer dışbükey çokgenlerden oluşuyor; çokgenlerin birbirleriyle bitişik olduğu düzenleme baştan başa aynı.”
Aynı defterde Escher, Haag’ın çokgen döşemelerinin taslaklarını da çizmişti. Bunları çalıştıktan sonra Haag’ın tarifindeki “dışbükey” kelimesinin gereksizliğini fark etti, döşemelerin şeklini değiştirerek dışbükey olmayan çok kenarlı döşeme örneklerini kolaylıkla elde ediyordu. Muhtemelen Haag’ın tanımındaki “dışbükey” kelimesine bu noktada parantezi koymuştu. Elbette “çokgen” kelimesinin kendi amaçları için tereddütsüz çok kısıtlayıcı olduğunu keşfetmişti, “şekil” veya “döşeme” kelimeleriyle kolaylıkla değiştirilebilirdi. Haag’ın tanımı (Escher’in düzeltmeleriyle) Escher tarafından ödünç alınmış ve bütün simetri araştırmaları için rehber olmuştu. Daha sonra bu tanımı kertenkele çiziminin arkasına dikkatle not etti (Çizim Escher’in Reptiles -Sürüngenler- isimli taş baskısında kullanıldı).
Polya’nın makalesinin Escher üzerinde büyük bir etkisi oldu. Escher düzlemin dört izometrisini (elle, mürekkeple) anlatan bütün metni ve Polya’nın düzlemsel döşemeleri simetri gruplarıyla sınıflandırmasını dikkatle not etti. Polya’nın bunun Fedorov tarafından 30 yıldan daha önce yapıldığından habersiz olduğu açıktır. Escher sezgisel olarak Polya’nın bahsettiği uyumu koruyan dönüşümlerden haberdardı, ama simetri gruplarına dair tartışmalardan hiçbir şey anlamamıştı. Onun esas olarak vurulduğu Polya’nın 17 düzlemsel simetri grubunu tasvir eden tam sayfa tablosuydu (Figür 1). Escher bu 17 çizimi tek tek defterine kopyaladı, bazılarını renklendirdi. Bunların arasında, El Hamra’da kaydetmediği simetrileri içerenler de vardı. Bunlar öteleme haricindeki içerdikleri simetriler, ötelemeli yansımalar ya da dörtte bir (90 derece) ve yarım dönüşlerden (180 derece) ibaret olanlardı. Bir ay süren çalışmasının ardından Escher, ilk kez dörtte bir dönüşlü simetriler içeren çizimlerini tamamladı: Dört ayağın birleştiği yerde bir dönüş oluşan, her seferinde birbiriyle bağlantılı dört kertenkele. Bu çizimlerinden bir parçayı, aynı ay içerisinde tamamlanan Development I (Gelişim I) isimli ahşap baskısının merkezinde kullandı.
Escher, Polya’nın çalışmasının kendisine sağladıklarına o kadar minnettardı ki, matematikçiye teşekkür etmek adına ona bir mektup yazdı. Polya’ya Development I isimli çalışmasının bir baskısını gönderdi ve matematikçiye konu hakkında uzman olmayanlar için, makalenin umut ettirdiği üzere, simetri hakkında bir kitap yazıp yazmadığını sordu. Bir yazar Polya’nın umut edilen kitabın yazılmadığını söyleyen yanıtını kibar ama resmi olarak nitelendirse de, Polya 1977’de bana Escher ile birden çok kez yazıştığını ve 1940’da Amerika’ya göç etmesi nedeniyle onunla bağlantıyı kaybetmekten ötürü pişman olduğunu yazmıştı. Şimdi Polya’nın Stanford Üniversitesi’ndeki arşivinde bulunan notları, mektupları ve çalışmalarıyla dolu unutulmuş bir bavulun yakın zamandaki keşfi, onun Escher’e, Escher benzeri bir çizim denemesini bile gönderdiğini göstermiştir. Bu belgeler arasında Polya’nın yılan desenli bir çizimi, Escher’in 1937 -1940 arasında yaşadığı adresiyle ve “MCE’ye gönder” alt notuyla bulunuyordu. Ayrıca Polya’nın hiçbir zaman bitirilememiş kitabı “Süslemenin Simetrisi”nin bir taslağı, planlanan kitap ve 1924 yılındaki makalesi için çok sayıda çizim taslağı da arşivde bulunuyordu.
Bir matematik araştırmacısı olarak Escher
Escher 1937’den 1941’e kadar, sadece matematiksel araştırmayla tanımlanabilecek bir yöntemsel sorgulamaya daldı. Haag’ın makalesi ona “düzlemin düzenli bölünmesi” gibi bir tanım sağlamıştı ve Polya’nın makalesi birçok şeklin bunları üretebileceğini göstermişti. Daha fazlasını bulmak ve tanımlamak istedi. Kendi tekniklerini kullanarak kovaladığı sorular şunlardı:
1) Her şeklin etrafı aynı şekilde sarılı olacak şekilde düzlemi uyumlu bir şekilde dolduracak düzlemin düzenli bölünmesi için olası şekiller nelerdir?
2) Böyle bir şeklin kenarları hangi yollarla izometriler ile ilişkilenebilir?
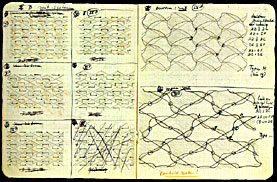
Escher’in bir figürü komşu bir figüre bağlarken kullanılmasına izin verdiği izometriler sadece ötelemeler, dönüşler ve ötelemeli yansımalardı; kullandığı canlı figürünün bir yüzünün doğal durumunun kullanılamadığı, düz bir kesit olması gerektiği yansımalar. 1941-1942’de düzlemin düzenli bölünmesi, bunların nasıl üretilebileceği ve renklendirilebileceğine dair birçok buluşunu, kendisinin kişisel ansiklopedisi olan nihai bir Defter’e kaydetti. Defter’in iki bölümü vardı. Kapağında, “Düzlemin asimetrik uyumlu çokgenlere düzenli bölünmesi; I Dört Kenarlı Sistemler MCE 1-1941 Ukkel; II Üç Kenarlı Sistemler X-1942, Baarn” yazıyordu.
Escher’in dörtkenarlı sistemler üzerine olan çalışması çok genişti. Bu döşemeleri, sembolik olarak, her bir figür bir paralelkenarı temsil edecek şekilde bir uyumlu paralelkenarlar ağı olarak gösterdi. Bu ağları her paralelkenar karşıt renkli diğeriyle bir köşe paylaşacak şekilde dama tahtası tarzında gölgelendirdi. Asimetrik figürler ilgisini çekiyordu (ne de olsa onun canlı figürleri esas olarak asimetrikti) ve asimetriyi sağlamak için her paralelkenarın içerisine bir çengel yerleştirdi. Çengel yönlendirmeyi sağlarken figürün sınırındaki küçük çemberler ve kareler figürün, komşu figüre dönebileceği iki katlı veya dört katlı merkezleri gösteriyordu. Escher kesin simetrinin özel paralelkenar ağları gerektirdiğinin farkındaydı ve bu yüzden 5 değişik kategori belirledi: Herhangi bir paralelkenar, eşkenar dörtgen, dikdörtgen, kare ve ikizkenar dik üçgen (köşegenlerin çizildiği kareler ağı). Bunları sırayla A’dan E’ye isimlendirdi. İki soruya cevap aradığından birkaç okul defterini, işe yaramayanları veya tekrar olanları yırtarak, döşeme figürlerini temsil eden işaretlenmiş ağ taslaklarıyla doldurdu. Düzlemin düzenli bölünmesini temsil eden işaretlenmiş bir ağı her bulduğunda kaydetti ve döşemenin şekil-figür kullanarak bir örneğini köşelerini harflerle işaretleyerek yaptı.

yazışmalarına konu olan Circle Limit III adlı çalışması.
Her figür köşesinin aynı figürle veya komşu bir figürle nasıl ilişkili olduğunu hızlıca kaydetmek için Escher kendi işaretini icat etti: = “öteleme ile ilişkili” demekti, II “ötelemeli yansıma ile ilişkili” demekti. Köşesinde bir S “180 derece dönüş ile ilişkili” ve L “90 derece dönüş ile ilişkili” anlamına geliyordu. Figür 2, sol tarafında 5 değişik “kare sistemleri”ni ve sağ tarafında bu sistemlerden ikisinin şekil içeren figürlerini göstermektedir. Escher’in sayfanın altındaki “Vorbeeld maken!” notu dikkat çekicidir: “Bir örnek yap!” Sonuçları, kelimelere ihtiyaç olmadan görsel olarak kaydedilmişti. Nihayetinde 10 değişik döşeme sınıfı bulmuş ve bunları I-X olarak numaralandırmıştı. Defter, çizimlerin hem görsel hem tanımlayıcı versiyonlarını içermektedir.
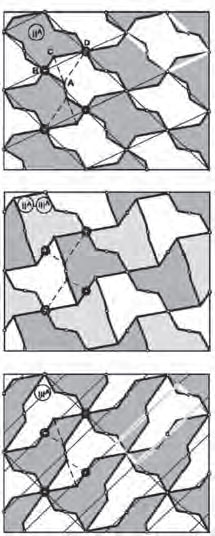
180 derece döndürülüyor.
Diğer düzenli bölünmeleri, haritalandırmak için 3 rengin gerektirdiklerini hâlâ keşfetmek adına Escher, “geçiş” adını verdiği bir teknik uyguladı. Figür 3, onun örneklerinden birinin tekrar çizimidir. 10 kategorisinden 2 renkli alışılageldik bir tanesiyle başlıyordu. Bu kategorilerde her seferinde 4 figür bir düğüm noktada birleşiyor ve sadece iki renge ihtiyaç duyuyordu. Daha sonra bir desen ve köşelerden birini (B diyelim) bir diğer dikkatle seçilmiş (A diyelim) sınır noktasına birleştiren, döşemenin düğümü olmayan bir sınır parçasını seçiyordu. A’yı bir dayanak noktası olarak kullanıyor, A ile B’yi birleştiren sınır parçasını döndürerek (bazen esneterek) B köşe noktasının sınır üzerinde kayarak yeni bir noktada durmasını sağlıyordu (C noktası). Aynı işlemin bütün desenlerin eşleşen sınır parçalarında tekrar edilmesi üç renkle gösterilebilecek yeni bir desen yaratıyordu (Figür 3b). İşlem yeni AC kesitinde C’yi orijinal desenin düğüm noktasına kadar sınır boyunca hareket ettirerek sürdürülebiliyordu. Bu tekrar 2 renge ihtiyaç duyan yeni bir desen oluşturuyordu (Figür 3c). (3 renkli) orta safhada figürlerin köşeleri kesinlikle özgün olan ile homeomorfik değildi, ancak şaşırtıcı olan sonuçta elde edilen (2 renkli) safhadaki yeni ağ da özgün ile homeomorfik olamayabiliyordu. Escher orta safhanın hem başlangıçtaki hem sonraki 2 renkli desenlerden bileşenler taşıdığını düşünerek onu her iki safhanın ismini kullanarak isimlendirdi. Figür 3’te, IIA sistemi IIA-IIIA’ya, o da IIIA’ya dönüşüyor. Bu anda, son desendeki figürlerin 4 değil 3 köşesi var ve bir düğüm noktasında 6 tanesi birleşiyor, Escher bunun bir istisna olduğunu not etmişti.
Escher bu keşiflerini kelimelere dökmedi, ama Defter’inde 16 sayfa boyunca bu 10 kategorinin tamamını kapsayan dönüşümlerin dikkatli tasvirlerini çizdi. Birçok seferinde aynı desenin bir belirgin dönüşümünden fazlasını keşfetti. Bugünün terminolojisini kullanırsak, tek bir izohedral döşemesinden yola çıkarak değişik izohedral tiplerinin nasıl üretilebileceğini keşfetmişti. Ayrıca bir çizelgede 10 kategorisinden hangilerinin diğerlerine öncülük ettiğini kaydetmişti. Bu çizelge, onun dönüşüm işleminin bir desenin topolojik ve kombinatorik özelliklerini dönüştürebileceğini ama simetri grubunu değiştiremeyeceğini açıklığa kavuşturmuştu.

Escher’in “dörtkenarlı sistemler”e dair çalışmasının son bölümü, “2 motifli” döşemeler olarak adlandırdıklarıyla ilgili 10 sayfadan oluşuyordu. 2 veya 3 renkli normal bir bölünmeyle başlayıp her figürü (aynı şekilde) iki ayrı şekil oluşturacak ve iki renkle gösterilebilecek şekilde ikiye bölerek devam ediyordu. Bu araştırma, “düalite” olarak adlandırdığına olan ilgisinden destekleniyordu; birçok çalışması figür ile zeminin oynadığı rolü değiştirme ya da karşıtların bitişikliği fikriyle yapılmıştı. Sky and Water I (Gök ve Su I) ve Circle Limit IV – Angels and Devils) (Çember Limit IV – Melekler ve Şeytanlar) ünlü örneklerdir.
Örneğin Sky and Water I’de (Figür 4) merkezdeki yatay olarak kenetlenmiş beyaz balık ve siyah kuşlar sırası çalışmayı üst ve alt yarılara ayırır (gök ve su). Bu merkez sıradaki balık figür, kuş zemin olabilir, tersi de geçerlidir. Ancak göz bu figür sırasından yukarılara kaydıkça varlıklar birbirinden ayrılır ve ayrı roller elde eder. Beyaz balıklar eriyip gökyüzünü oluştururken siyah kuşlar yükselerek üç boyutlu olurlar. Balık uçan kuşların arka planına dönüşür. Göz merkez figür sırasından aşağıya kaydıkça, tam tersi bir dönüşüm gerçekleşir. Bu sefer balık üç boyutlu bir şekil kazanır, siyah kuşlar çözülerek balıkların yüzeceği suya dönüşür. Matematikte çift nesne fikrinin özü, birinin diğerini tamamen tanımlamasıdır, bir küme ve eşleniği ya da bir önerme ve negatifi gibi. Figür-zemin düalitesinin yanı sıra aynı resimde başka çeşit düaliteler de temsil edilmektedir: siyah ve beyaz, gökyüzü ve deniz gibi. Ve karşıtlar: kuş ve balık çoğunlukla karşıtlığı ifade ederler ve çalışmada her kuş, suyun görünmez yüzü ayna rolü oynarken, bir balığın tamamen karşısına konmuştur.
Escher’in Defter’inin ikinci bölümü kısadır, “üçgen sistemler” olarak adlandırdıklarıyla ilgilidir; 120 derece dönüş merkezleri olan düzenli bölünmeler (A sistemi), ya da 60 derece, 120 derece ve 180 derece dönüş merkezleri olanlar (B sistemi). Dönüş merkezlerinin yerleşimini açıkladıktan sonra, sadece 20 farklı döşemeyi kaydeder; çoğunluğu iki motiflidir ve hepsi dikkatlice simetriye uygun olarak renklendirilmiştir. Çoğunluğu 3 renge ihtiyaç duyar. Dörtkenarlı sistemlerinin aksine figürlerinden bazıları dönüş simetrisine sahiptir ve bunlardan bir ya da iki motifli diğer figürleri elde eder.
1941’de bu araştırmalarının sonuna yaklaşırken Escher ve ailesi, ömrünün kalan son 2 yılı haricindeki tamamını geçirmek üzere Hollanda/Baarn’a taşındılar. Takip eden yıllarda, her biri numaralı ve dikkatlice çizilmiş, figürleri mürekkeple çizilmiş, renklendirmesi suluboyayla yapılmış 100 düzlemin düzenli bölünmesi örneği üretti. Simetri çizimleri portfolyosu genişledikçe bunları “çizim deposu” olarak adlandırmaya başladı. Bu çizimlerden bazı bölümlere birçok çalışmada, not kartında, duyurularda, boyanmış ve döşenmiş kamusal çalışmalarda ve hatta bir küre üzerinde bile yer verildi. Hepsinde 134 numaralandırılmış simetri çizimleri ve birçok numaralandırılmamış taslak bulunuyordu.
Escher sanatında etkiler yaratmak adına başka birçok küçük matematik araştırması yürüttü. Bazı sonuçlar Düzlemin Düzenli Bölünmesi: Soyut Motifler, Geometrik Problemler başlıklı bir deftere kaydedildi, diğerleri küçük yapraklarda toplandı. Birçok Mağribi tarzı desenle uğraştı ve bağlantılı halkalar üzerine çalıştı (son çalışması Yılanlar’da görülebilir). Banknotlar tasarlarken benzer üçgenlerden oluşan çok sayıda desen kullandı. Ayrıca açıkça keşfettiği ama ispatlayamadığı iki teoremi kayıt altına aldı. Bir tanesi üçgendeki kesişen kenarlarla ilgiliydi, diğeriyse özel bir altıgen figürünün kesişen köşegenleriyle ilgiliydi. Talebimle birlikte birinci teorem A. Liu ve M. Klamkin tarafından, ikincisi ise J. F. Rigby tarafından doğrulandı.
Escher’in matematikçilerle etkileşimleri
1954’e kadar Hollanda dışında çok az matematikçi Escher’i tanıyordu. O yıl, Uluslararası Matematikçiler Kongresi Amsterdam’da yapıldı ve N. G. de Bruijn, Stedelijk Müzesi’nde Escher’in baskılarını, simetri çizimlerini ve oyulmuş toplarını içeren bir sergi düzenledi. Katalog’da “Muhtemelen matematikçilerin sadece geometrik motifler ilgisini çekmeyecek, genel olarak matematikte de ortaya çıkan ve birçok büyük matematikçinin konularına ait alışılmadık cazibe kaynağı olan oyunculuk da önemli bir etken olacak” diye yazıyordu.

Roger Penrose sergiyi ziyaret ettiğinde şaşırmış ve meraklanmıştı. Escher’in “Görelilik” isimli baskısı özellikle gözüne çarpmıştı. Birçok farklı bakış noktasından görülebilecek şekilde, birkaç insanın yerçekimi kanununa kafa tutarak imkânsız bir şekilde aynı anda tırmandığı veya indiği üçgen formda düzenlenmiş üç merdiveni (ve daha küçük merdivenleri) gösteriyordu. Penrose’a, parçaları kendi başına tutarlı ama birleştiğinde “imkânsız” bir yapı bulmak için ilham oldu. İngiltere’ye döndükten sonra şimdi ünlü olan, birleşerek bir üçgen oluşturur gibi görünen karşılıklı olarak dik çubuklar içeren Penrose üçgeni fikriyle ortaya çıktı (Figür 5). Bundan sonra babası, kâğıt üzerinde çizilebilen ama inşa edilmesi imkânsız bir diğer nesneyi, “sonsuz merdiven”i buldu. Penrose, bu imkânsız nesnelerin taslaklarını Escher’e göndererek keşif halkasını tamamladı. Escher Waterfall (Şelale) isimli eserinde aralıksız hareketi, Ascending and Descending’te (Çıkış ve İniş) keşişlerin bitmeyen yürüyüşünü kullanacaktı.
Penrose 1962’de Escher’in evini ziyaret etti ve 60 derecelik özdeş eşkenar dörtgenden türetilmiş ahşap puzzle parçaları hediye etti. Escher daha sonra Penrose’a parçaların bir araya getirilebildiği tek yolu içeren puzzle’ın çözümünü gönderdi. Burada uyumlu figürler iki farklı şekilde sarılmıştı. 1971’de Escher düzenli bölünme olmayan bir figürle (bugün 2-izohedral olarak adlandırılır) tek desenini yaptı. Penrose’un puzzle’ının kurallarına göre düzlemi dolduran küçük hayaletiyle bu çizim, Escher’in numaralandırılmış simetri çizimlerinin sonuncusuydu.
H. S. M. Coxeter de ilk kez 1954’te Escher’in çalışmalarını görmüştü ve Kanada’ya döndüğünde Escher’e bir mektup yazarak sanatçının çalışmalarına duyduğu minnettarlığı ifade etmişti. 3 yıl sonra, sanatçının simetri çizimlerinden ikisini, Kanada Kraliyet Topluluğu’na yazacağı bir makaleyi resimlendirmek için kullanıp kullanamayacağını sormak için tekrar Escher’e yazdı. Makale Öklit uzayında ve hiperbolik düzlemin ve küre yüzeyinin Poincaré disk modelinde simetriyi tartışıyordu. Escher seve seve kabul etti ve daha sonra makalenin bir kopyası eline ulaştığında Coxeter’e “Bazı çizimler ve özellikle sayfa 11’deki figür bana büyük bir şok yaşattı” diye yazdı. Figürün boyutları küçülen ve bir çemberin sınırlarında teorik olarak sonsuza kadar tekrar eden üçgen şekilleriyle hiperbolik döşemesi, Escher’in sonsuzluğu sınırlı bir alanda yakalamak için tam olarak aradığı şeydi.

Escher figür üzerinde pergel ve cetvelle çalıştı ve önemli noktaları çember içerisine aldı (Figür 6). Buradan Circle Limit I (Çember Limit I) isimli eserini üretebilecek kadar geometriyi ayırt etti. Ancak daha fazla öğrenmek istiyordu ve Coxeter’e ne anladığını, yani 6 çemberin merkezlerinin yerlerini işaretleyerek gönderdi (Figür 7). Bu mektupta Coxeter’den kibarca “limite ulaşana kadar merkezlere (sınırı belirleyen çembere) dışarıdan yaklaşan (geriye kalan) çemberleri oluşturmak için bir basit açıklama” talep etti. Ayrıca “bir çemberin limitine ulaşan bunun dışında başka bir sistem” olup olmadığını sordu. Coxeter, Escher’in ilk sorusuna kısa bir yanıt verdi:
“Çiziminizde sayfanın arkasında kırmızı bir ‘o’ [+ işareti] ile işaretlediğim nokta, çemberlerinizden merkezleri 1, 4, 5 olanlarla birlikte uzanıyor. Dolayısıyla bu merkezler (solgunca kırmızı ile çizdiğim) [kesik çizgi ile] düz bir çizgi üzerinde uzanıyorlar ve kırmızı nokta [+ işareti] içerisinden geçen dördüncü çemberin de merkezi bu aynı çizgi üzerinde olmalı.”
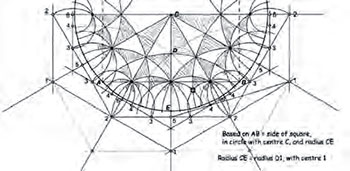
Escher’in bütün şemayı buradan oluşturması gerekiyordu. Tam tersine, Coxeter ikinci soruya, başında “Evet, sonsuz kadar çok!” diyerek uzun bir yanıt verdi ve daha sonrasında Generators and Relations (Üreticiler ve İlişkiler) metnine referansla hangi desenlerin var olduğunu açıkladı.
Escher bu yanıttan dolayı hayal kırıklığına uğramıştı, ama bu sadece konuları anlamak noktasındaki kararlılığını artırmıştı. Oğlu George’a şunları yazdı:
“[Coxeter] her şey için 3 ve 7 değerlerini kullandığı bir örnek göndermiş. Ama bu tek sayı 7 benim için tamamen işe yaramaz; ben iki ve dördü (ya da dört ve sekizi) arzuluyorum. Bu çeşit resimlere karşı olan ilgim ve bu çalışmayı kovalamak için sahip olduğum kararlılık belki de sonuçta tatmin edici bir çözüme neden olacak. (…) Öyle görünüyor ki, Coxeter için bir ‘alaylı’nın anlayabileceği şekilde yazmak çok zor. Sonuç olarak ne kadar zor olursa olsun böyle bir problemi kendi sakar tarzımda çözmekten daha büyük tatmin alacağım.”
Escher kendi hiperbolik desen çalışmalarına, kendi tanımladığı şekliyle “Coxeterleştirme” işlemine başarıyla devam etti ve 1959-1960’ta üç farklı Circle Limit baskısı üretti. Coxeter Circle Limit I’i aldığında Escher’i “açı koruyan” desene dair anlayışı için övdü. 1960’ta da karmaşık Circle Limit III’ü aldığında Escher’e, içine semboller serpiştirilmiş, birçok teknik metne referans içeren, çalışmanın matematiksel içeriğini açıklayan 3 sayfalık bir mektup gönderdi. Escher George’a ümitsizlikle “Benim gerçekte ne yaptığıma dair 3 sayfalık bir açıklama… Hiçbir şey, tamamen hiçbir şey anlamamam ne yazık” diye yazmıştı.

Coxeter 1960’ta Escher için çalışmalarıyla ilgili Toronto Üniversitesi’nde iki ders ayarladı ve onu evinde ağırladı. Coxeter-Escher yazışması birkaç yıl boyunca devam etti. 1964 Mart’ında Coxeter, “Çalışma duvarımdaki Circle Limit III’e tekrar tekrar baktıkça, sonunda fark ettim ki, ekte, kitabına ilişkin Mathematical Reviews’daki yorumumda görebileceğin gibi, onun sonsuzluğuna dair olumsuz düşüncemin yanlış anlamamdan kaynaklandığını fark ettim” diye yazdı. “Çalışmana baktıkça daha çok hayran oluyorum” diye ekledi. Bu yorumla Coxeter ilk kez, balıkların omurgalarını oluşturan beyaz kemerlerin onun ve başkalarının farz ettiği gibi kötü bir şekilde birleştirilmiş hiperbolik çizgiler değil, eşit uzaklıktaki eğrilerin dalları olduğunu ortaya çıkardı. 1979’ta ve tekrar 1995’te, bu beyaz kemerlere adanmış daire çevresini aynı açıda, yani 80 derecede kesmesi gerektiğini (ve gerçekten büyük bir doğrulukla kestiğini) anlatan makaleler yayımladı. Yani Escher’in sezgiye dayanan çalışması, herhangi bir hesaplama olmadan, mükemmeldi.
Coxeter diğer makalelerde Escher’in çalışmasına dair matematiksel analizler yaptı ve sanatçının bazı buluşlarının önünü açtığını işaret etti. 1964 Mayıs’ında Escher Coxeter’e Square Limit (Kare Limit) isimli çalışmasını gönderdi ve arkasında yatan kendiliğinden benzer üçgenler ağını bir diyagramla açıkladı (Figür 8). Escher’in, kırmızı ve mavi (açık ve koyu griyle görülüyor) kalemle yapılmış açıklayıcı taslağı grafik kâğıdı üzerindeydi. Bölme işleminin sonsuza kadar sürdürülebileceğini göstermek için merkez kareyi saran ilk üç halkayı gösteriyordu. Bu fraktal yapıyı kendiliğinden tasarladı ve bir Öklid yapısının düz parçalarına sahip olsa da, Circle Limits çalışmasında istenen özelliği gösteriyordu; sınırlayan kareye ulaştıkça figürler küçülüyordu. Diyagramın ortasındaki 90 derece dönüş, kırmızı (açık gri) şekilleri maviye (koyu gri), mavileri (koyu gri), kırmızıya (açık gri) ve beyazları beyaza gönderen bir renk simetrisiydi. Escher’in çalışmasında üçgenler balıkla yer değiştirmişti.
Escher’in diğer matematikçilerle de kısa etkileşimleri olmuştu, ama hiçbiri onun çalışmasını Polya, Penrose ve Coxeter kadar etkilemedi. A. Speiser’in doktora öğrencisi Edith Müller, bana, Escher’in kendisinin El Hamra çinileri üzerine yaptığı çalışmadan haberdar olduğunu ve onu 1948’te Zürih’te çalışmasını tartışmak üzere ziyaret ettiğini söylemişti. Ona, Speiser’in simetriyi daha iyi anlamak için nasıl dantel yapmayı öğrendiğini anlatmıştı.
Speiser’ın bir diğer öğrencisi Heinrich Heesch 1930 ortalarında çiniler üzerine geniş araştırmalar yürütmüş, ancak 1960’lara kadar yayımlamamıştı. O da düzenli çinileri, her figürün aynı şekilde sarılı olduğu, benzer figürlerle düzlem doldurma olarak tanımlamıştı. Ayrıca Escher gibi bu şekilde bağlantılandırılan ve yansıma simetrisi olmayan asimetrik figürlerin köşelerindeki koşulları karakterize etmekle ilgiliydi. Tam olarak 28 çeşit bu tür figür olduğunu ispatladı ve 1963’te Otto Kienzle ile birlikte yazdığı kitabında, bunların bir görsel çizelgesini gösterdi. Kitabı, o dönemde çok hasta olan Escher’e gönderdi; fakat Escher için bu bilgi kendi keşiflerinden 20 sene sonra gelmişti.
Escher’in yaşamının kalan iki yılında, matematik öğretmeni Hans de Rijk, sanatçıyla, çalışmasının arka planında yatan matematiği özel bir dikkat göstererek yorumlayan bir kitap yazmak için işbirliği yaptı. Her pazar kaçırmadan birlikte zaman geçirdiler. Bu kitabın ve Escher’in grafik çalışmasına dair açıklayıcı bir katalogun her ikisi de 1976’da, sanatçının ölümünden 4 yıl sonra yayımlandı ve Escher’in bazıları geometrik birer mucize olan baskılarının zahmetli ilksel çizimleri ilk kez gözler önüne serildi.
Escher’in çalışmaları matematiksel fikirlerin öğretilmesinde kullanıldı
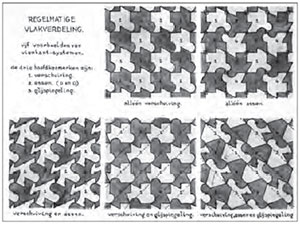
Escher öğretmenlik rolünü seviyordu; farklı türden dinleyicilere dersler verdi; bilimsel toplantılarda, öğrencilere, müze ziyaretçilerine, hatta Rotary Kulüpleri’nde bile. Derste kullandığı poster (Figür 9), beş farklı tasvirde bir figürü başka bir figüre dönüştürürken ötelemelerin, dönüşlerin ve ötelemeli yansımaların etkinliğini nasıl anlattığını gösterir. Sayılar bir figürün çeşitli yönlerini tanımlar, çemberler ve kareler iki katlı ve dört katlı dönüş merkezlerini sırasıyla tanımlar ve komşu kesik çizgiler bir figürün kayabileceği ve (eşit uzaklıkta bir çizgide) daha sonra yansıyabileceği raylar olarak rol oynar. Escher izometrilerin nasıl hareket ettiğini gösterebilmek için bu figürlerin şekillerinde düzleştirilmiş tel askılarda parlak renkli mukavva kesiklerini kullanmıştır.
Escher’in kitabı 1960’ta Hollanda’da yayımlandığında önsözde kristalograf P. Terpstra’nın, simetriye ve 17 düzlemsel simetri gruplarına dair kısa bir yazısı bulunuyordu. İngilizce çeviride yayımlanan bu yazı ayrı bir kitapçık gibiydi, Amerikan baskısında hiç bulunmuyordu. Açıktır ki yayıncı, Escher gibi, çok teknik olduğunu düşünüyordu.
Amsterdam Üniversitesi’nden kristalograf Caroline MacGillavry, Escher’in sanatının bir metinde öğretim aracı olarak kullanılma ihtimalini gören ilk biliminsanıydı. 1950’lerin sonlarında stüdyosunu ilk kez ziyaret ettiğinde hayranlık duydu: “‘Alaylı teorisi’ni not ettiği defteri benim için vahiy gibi oldu. Pratikte, ötelemeli yansıma içersin veya içermesin, 2, 3 ve 6 renkli bütün dönüşsel iki boyutlu grupları içeriyordu.” Bu ziyaret, öğrenime yeni başlayan jeoloji öğrencilerine renkli periyodik desenlerin simetrilerine göre sınıflandırılmasını öğretmek için Escher ile işbirliği yapma fikrinin doğmasına yol açtı. Uluslararası Kristalografi Birliği yayına sponsor olmayı kabul etti. MacGillavry kitabın önsözünde şunu not etti:
“Escher’in periyodik çizimleri, simetriyi öğretmek için harika bir materyal. Bu desenler, kristalografi sınıflarının öğretmenleri tarafından tahtaya çizilen atom rolü yapan beceriksiz küçük çemberler dizisiyle belirsizleşmiş öteleme ve diğer simetrilerin temel kavramlarını, açıkça tasvir etmek için yeterliydi. Diğer taraftan tasarımların çoğunluğu alanda yeni başlayan bir öğrenci için çok büyük zorluk göstermiyordu.”
Escher’in periyodik çizimler deposunu gözden geçirirken hiçbir renk simetrisi olmayan en basit simetri gruplarından birinin temsil edilmediğini fark etti. Onun isteği üzerine Escher boşluğu doldurmak üzere yeni bir simetri çizimi üretti. Ayrıca gene talep edilen bir başka tipi üretti ve bazı başkalarını yayımlanması için tekrar çizdi.
Coxeter muhtemelen (Hollanda dışında) Escher’in çalışmasını bir matematik metnini tasvir etmek için kullanan ilk matematikçiydi. Introduction to Geometry (Geometri’ye Giriş) 1961’de ilk yayımlandığında, Escher’in simetri çizimleriyle tasvir ettiği simetriyi ve düzlemsel mozaikleri içeren, standart olmayan konularıyla alışılmadık bir kitaptı. Martin Gardner Scientific American’daki “Matematik Oyunları” köşesinin bir tanesini kitabın tanıtımına ayırdı ve çizimleri tekrar yayımlayarak Escher’in çizimlerini bilim dünyasının ilgisine sundu. Bu, çeşitli düzeylerde matematik öğretmeye yönelik metinlerin ve makalelerin Escher’in periyodik çizimlerini kullanmasından çok önce değildi. Düzlemsel izometriler, benzerlikler ve simetrinin temel kavramları Escher’in simetri çizimlerinin harika tasvirler sağladığı belirgin konulardı, ama çizimler soyut cebir ve grup teorisinin yüksek düzey kavramlarının öğretilmesinde de kullanılabiliyordu. Majorie Senechal, Escher’in periyodik çizimlerindeki renkli simetri gruplarını çalışarak bir grubun tanımını, değişmeli olup olmadığını, grup etkisini, yörüngeleri (orbitleri), üreteçleri, altgrupları, kosetleri, eşlenikleri, normal altgrupları, stabilizatörleri, permütasyonları ve permütasyon gösterimlerini ve grup genişlemelerini öğrencilerin nasıl daha iyi anlayabileceğini tartışıyordu.
Matematik ve bilim öğretmenleri (ve metinleri) Escher’in baskılarını, matematiksel nesnelerin (düğümler, Möbius şeritleri, spiraller, loksodromlar, fraktallar, çokyüzlüler, uzay bölümleri) sanatsal tasvirleri için ve soyut matematiksel kavramlar (sonsuzluk, düalite, yansıma, görelilik, kendine göndergeli önerme, rekürsiyon, topolojik değişim gibi) için ilgi çekici görsel metaforlar sağlamak amacıyla kullanıyor. Pulitzer Ödülü kazanan Gödel, Escher, Bach: Bir Ebedi Gökçe Belik adlı kitabında Douglas Hofstadter, rekürsiyon ve kendine göndergeli önerme kavramlarını ifade etmek için Escher’in çalışmasını kullandı. Daha birçok yazar Escher’in baskılarını algı ve illüzyona ait karmaşık fikirleri tasvir etmek için kullandı.
Sanatı yorumlayanlar yorumlarına sanatçıların niyet okumalarını eklerler. Matematikçilerin Escher’in çalışmasını sonsuzluk fikrini ve diğer matematiksel kavramları tasvir etmek için kullanması sorgulanabilir. Ancak Escher’in bu kavramlarla el altından uğraştığı ve birçok çalışmasını oluştururken kullandığı not edilmelidir. Sonsuzluğa duyduğu hayranlık ve onu nasıl yakalayabileceği tekrar tekrar döndüğü bir konuydu. Sorgulamasını “Sonsuzluğa Yaklaşımlar” isimli eserinde ustalıkla anlatmıştır:
“İnsanın elinden zamanın bir gün durabileceğini hayal etmek gelmez. Bizim için, bu dünya kendi ekseni etrafında ve Güneş’in etrafında dönmeyi bıraksa da, artık günler ve geceler, yazlar ve kışlar olmasa da, zaman sonsuza kadar akmaya devam edecek.
“Durmadan daha ileriye ve daha ileriye, hem zaman hem uzayda sonsuzluğa dalan kimse sabit noktalara, kilometre taşlarına ihtiyaç duyar; yoksa hareketi durağanlıktan ayırt edilemez. Takip edebileceği yıldızlar, hareketini ölçmek için deniz fenerlerine ihtiyaç vardır. Evrenini verilen uzunluklarda uzaklıklara bölmeli, bitmez bir ardışıklıkla tekrarlayan bölmelere ayırmalıdır. Bir bölmeden diğerine geçerken saati tik-tak eder.”
Escher için matematiksel kavramlar, özellikle sonsuzluk ve düalite, sanatsal ilham için sabit birer kaynaktı.
Escher’den etkilenmiş ve ilham almış matematiksel araştırmalar
Escher’in çalışmasının çeşitli yönleri bilim topluluğunun üyelerine teorik araştırmalarda on yıllardır yol gösterici olmaktadır. Ve çalışmalarından bazıları matematiksel araştırmalara doğrudan ilham vermiştir. Buraya bu araştırmaların bir kısmını (zorunlu olarak kısaca) not ediyoruz.
“Düzenli” desenlerin figürlerin köşelerine bağlı ilişkilere göre sınıflandırılması Escher’in ve aynı zamanda H. Heesch’in yöntemiydi, ancak yansıma olmayan simetri grupları içeren asimetrik figürler ve desenlerle sınırlıydı. 1970’lerde Branko Grünbaum ve Geoffrey Shephard desenin simetri grubuna göre geçişlilik özelliğine ilişkin çok çeşitli desenlerin sistematik sınıflandırmasını çalıştı – izohedral (figür-geçişli), izogonal (tepe geçişli), izotoksal (köşe geçişli). Yöntemleri, her figürün etrafının nasıl sarıldığını kaydetmek için bitişiklik ve oluşum sembolleri kullanmaya dayanıyordu; geçişlilik şartı her figürün etrafının aynı şekilde sarılmasını gerektiriyordu. Çalışmaları, desenlerin tüm yönleriyle ilgili temel referans kitabı olarak kalmıştır.
2 renkli ve 2 motifli desenler Escher’in düaliteyi anlatmak için kullandığı yollardı. 2 renk simetri gruplarının ilk sınıflandırmasının 1936’da tekstil tasarımları için bu siyah beyaz mozaiklerle ilgilenen H. J. Woods tarafından yapıldığını not etmek (neredeyse aynı zamanlarda Escher kendi bağımsız araştırmasını yapıyordu) ilginçtir. Monohedral (bir figürlü) desen iki renkli olarak kullanıldığında ve desenin simetrisi, figürleri ve renkleri değiştirildiğinde buna “karşıt değişme simetrisi” diyordu (Örneğin düzlemin satranç tahtası gibi karelerle renklendirildiği bir desende, desenin, bir kare sütununun köşesindeki yansıması karşı değişme simetrisidir). Bilim topluluğu ve Escher’in, Woods’ın çalışmasından haberi yoktu. Daha sonra, Escher’in çalışmasında da çok baskın olan bu tür simetri, Rus kristalograflar tarafından “anti-imetri” olarak adlandırıldı. Bu terminoloji günümüzde kullanılmamaktadır. Escher bazı kristolografların antisimetri kavramını kabul etme konusunda sorunları olduğunu, ama kendisinin onsuz yapamadığını not etmişti.
Escher’in, figürleri 2 motifli desenler elde etmek için bölmesinin güçlü bir yöntem olduğu gösterilmiştir. Bugün, 2-izohedral terimi desenin simetri grubunun iki yörünge yarattığı desenleri tanımlamak için kullanılır – desenin simetri grubuna göre birbirinden ayrı 2 figür sınıfı bulunmaktadır. Her 2-izohedral desenin, bir izohedral desen ile başlanıp kesme ve yapıştırma işlemleriyle türetilebileceği ispatlanmıştır ve bu aynı işlem k-izohedral desenler üretmek için genişletilebilir. Andreas Dress ve ben bu desenlerin diğer yönleriyle ilgili çalıştık.
Renk simetrisi 1950’lere kadar kristalografların ciddi bir ilgi alanı değildi; sonraları bile kolaylıkla benimsenmedi ve renk simetri gruplarının sistematik olarak çalışılması için uzun yıllar gerekti. Kristalograflar ve matematikçiler renk simetri gruplarını araştırmaya başladıklarında tasvirler ve keşifler için (Caroline MacGillavry gibi) Escher’in çalışmalarına döndüler. Bugün bile renk simetri grupları için birbiriyle yarışan notasyonlar vardır.
Metamorphosis ya da topolojik değişim Escher’in çalışmalarındaki anahtar temalardan biriydi. Birbirlerine bağlanmış varlıkları çoğunlukla paralel kenar olarak başlıyordu; kareler, üçgenler ya da altıgenler, Plate I’deki görsel gösterimindeki gibi sorunsuz bir şekilde arkada yatan örgüyü koruyarak tanıdık şekillere dönüşüyordu. Başka eserlerde varlıkların metamorfozu, Metamorphosis III’te görülebileceği gibi örgüyü de değiştiriyordu. William Huff’ın tasarım stüdyosu örgü yapısını koruyan ilgi çekici “parke deformasyonu” örnekleri üretmiştir ve daha yakın bir zamanda Craig Kaplan, Escher tarafından yapılan deformasyon çeşitlerini araştırmıştır.
Yüzeyleri simetrik desenlerle kaplama Escher’in tutkusuydu -Öklid düzlemi, hiperbolik düzlem, küre yüzeyleri ve silindirler- ve her zaman bu kaplamalar desenli yüzeylerin önemsiz olmayan simetri gruplarını temsil ediyordu. Douglas Dunham, Escher tarzı hiperbolik düzlem desenlerini ve onları bilgisayarda nasıl gösterebileceğini araştırdı. Başkaları farklı yüzeylerin nasıl periyodik tasarımlarla kaplanabileceğini çalıştı ve bazen “Hangi simetri grupları bu kaplamaları temsil ediyor?” diye sordular.
Escher’in dekore edilmiş karelerle desenler üretme algoritması, matematikçilere ve bilgisayar bilimcilerine çalışmalarını tetkik etmek ve sorulara yanıt vermek için kombinatorik teknikleri ve bilgisayar tekniklerini kullanma konusunda ilham verdi. Başka sorular da sorulmuş ve yanıtlanmıştır.
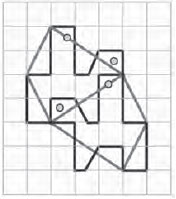
Figür şekiller üretmek Escher’in neredeyse bir saplantısıydı. Düzenli bir bölünme üretebileceğini bildiği tek bir figürle başlayabiliyordu (çoğunlukla bir çok kenarlıyla) ve sonra sınırı büyük zahmetle tanınan bir şekle çeviriyordu. Escher’den başka kim Figür 10’daki çokgeni miğferli bir atlıya benzetebilirdi ki?
“İki komşu şekil arasındaki sınır çizgisinin ikili bir işlevi vardır, böyle bir çizginin izini sürmek karmaşık bir iştir. Her iki tarafında da, aynı anda, bir tanınırlık ortaya çıkar. Ancak insan gözü ve zihni aynı anda iki şeyle meşgul olamaz ve bu yüzden bir taraftan diğerine hızlı ve sürekli bir atlama olmalıdır.”(5)
Escher’in işlemini bir bilgisayar programıyla gerçekleştiren ilk kişi Kevin Lee’ydi. Craig Kaplan ve David Salesin tamamlayıcı bir soruya karşılık olarak bir bilgisayar programı oluşturdular; herhangi bir şekille başlanarak, bu şekil kibarca deforme edilerek (hâlâ tanınır şekilde) izohedral desen oluşturabilecek bir figüre dönüştürülebilir mi?
Düzenliliğin yerel ve küresel tanımı Escher’in ilgi alanında değildi, her figürün aynı şekilde çevrelenebileceği yönündeki yerel kuralı takip etti. Ancak Escher’in “düzenli bölünme”lerinin her biri bir izohedral desendi; simetri grubunun figürler üzerinde geçişli olduğu yönündeki evrensel düzenlilik şartını sağlıyordu. Bir izohedral desen yerel düzenliliğe sahip olmak zorunda mıdır, bu iki tanım denk midir? Öklid düzleminde, evet, en azından asimetrik figürler ve çokgenlerle köşeden köşeye desenler için, ama hiperbolik düzlemlerde veya daha yüksek boyutlarda olduğu gibi değil. P. Engel de bu soruya yanıt arar.
Kendi deseniyle simetri üreten bir figürün simetrisiyle Escher tarafından yüzleşilmiş ve not edilmişti. Yansıma simetrisine sahip bir figür kullandığında (ejderha gibi), desenlerin simetrileri benzeri yansımalara neden olmuştu. Figürün simetrik olduğunu not etmiş ve sınıflandırma sembolünün yanına bir yıldız işareti koymuştu. Ancak birkaç örnekte figürün neredeyse simetrik (ya da küçük bir değişimle simetrik olabilecek) olduğu, ancak figür için yansıma çizgisinin desenlerden herhangi biri için yansıma çizgisi olmadığı bir desen yarattı. Branko Grünbaum bu tarz figürlere “hipersimetrik” adını vermiş ve karakterize edilip edilemediklerini sorgulamıştır. Bu yanıtlanmamış bir sorudur.
Simetri grupları tarafından oluşturulmayan düzenlilik Escher’in çalışmalarında en azından iki kez ortaya çıkmıştır: Azalan boyutlardaki karelerin fraktal konstrüksiyonunda ve kombinatorik olarak kusursuz ama renk simetrisi olarak kusursuz olmayan kelebeklerle yaptığı en karmaşık tasarımlarından birinde. Branko Grünbaum sadece simetri grupları tarafından tanımlananlar haricinde, diğer desenlerde ve çizimlerde farklı “düzenlilik”lerle ilgili ciddi çalışmalar yapmıştır.
Escher’in litografı “Print Gallery”yi tamamlamak H. Lenstra ve B. de Smit için yakın dönemde bir matematiksel meydan okuma oldu. Arka planda yatan geometrik “ağ”ı nasıl anladıkları, nasıl çözdükleri, çözülmüş çizimdeki eksik harfleri nasıl tamamladıkları ve tekrar nasıl oluşturdukları bir makalede anlatılmıştır.
1960’ta Escher “gerçek bilimlerde hem öğretim hem bilgi olarak cahil olsam da, meslektaşım sanatçılara kıyasla matematikçilerle daha çok ortak noktam bulunuyor” demişti. Bir öğrenci olarak matematikle çatışmış olsa da, bir grafik sanatçısı olduğunda matematiksel araştırma yürütmeye, yeni geometrik fikirler öğrenmeye, matematiksel kavramları tasvir etmeye ve matematikle ilgili sorular sormaya itilmişti. Çalışmalarının bilim topluluğu için yarattığı etkinin ölçeğini tahmin bile edemezdi.
Dipnotlar
1) G. Escher, “M. C. Escher at work”; H. S. M. Coxeter, M. Emmer, R. Penrose, and M. L. Teuber, eds. M. C. Escher: Art and Science, North-Holland, Amsterdam, 1986 içinde, s.1-11.
2) F. H. Bool, J. R. Kist, J. L. Locher, and F. Wierda, M. C. Escher: His Life and Complete Graphic Work, Harry N. Abrams, New York, l982, Abradale Press, 1992, s.15.
3) Escher’in çalışmalarından oluşan 1995’de Ottawa’da Kanada Ulusal Galerisi’nde düzenlenen bir serginin başlığı “M. C Escher: Doğa Manzaralarından Fikir Manzaralarına”ydı.
4) ) Escher’in renkli düzlem doldurma çalışmaları mozaik, periyodik çizimler, çini ve simetri çizimleri olarak adlandırılıyor; ben simetri çizimleri tanımını tercih ediyorum.
5) C. H. MacGillavry, Symmetry Aspects of M. C. Escher’s Periodic Drawings, Oosthoek, Utrecht, 1965, s.7.










