Pi sayısı matematik bahçesinin en zarif çiçeklerinden birisidir. Archimedes’den beri yüzlerce yıldır matematikçilerin ve diğer biliminsanlarının merak ve ilgiyle kokladıkları bir çiçek olagelmiştir. Bu sayının birçok özelliği vardır: Transandant (aşkın) yani katsayıları tam sayı olan polinomun kökü olamayan sayıdır. Bunun ispatı 1882’de Ferdinand von Lindemann tarafından yapılmıştır. İspatı, iki yüz yıllık önemli matematiksel katkıları temel almıştır. Matematik literatüründe karşımıza çıkan ve matematikçiler tarafından estetik özelliğinden pek çok söz edilen eiπ+1 = 0 eşitliği, matematiğin en önemli sabit sayıları olan e, i,pi, 1 ve 0 sayılarını içermesi açısından oldukça ilginçtir. pi’nin hesabı için çok değişik yöntemler kullanılmakla birlikte günümüzde yakınsak sonsuz seriler, çarpımlar ve ardışık yineleme bağıntıları kullanılmaktadır. Kaynakçadan bu yöntemlere erişilebilir.
Binlerce yıldır insanlar Pi’nin daha çok ondalık basamağını hesaplamaya çalışmaktadır ve bu ondalık basamakların nasıl bir dağılım gösterdiği merak konusudur.
pi’ye duyulan bu ilgi nereden kaynaklanmaktadır? pi’nin bugüne kadar bilinen özelliklerinden daha başka keşfedilmeye hazır hangi özellikleri vardır? Matematik bahçesinin en zarif çiçeği orada durmakta ve belki de sonsuz özelliklerini sunmaya hazır bir sevgili gibi beklemektedir.
Hemen hemen tüm matematik kitaplarında, özellikle matematiğe ilgi duyan kişilerin okuması için yazılan kitaplarda pi’nin özelliklerinden söz edilmeden geçilmemiştir.Pi’nin geometri, olasılık, diferansiyel ve integral hesaplamalarında nasıl farklı bir biçimde kullanıldığını görmek gerçekten ilginçtir.
Niye biri bugün süper bilgisayarlarla yapıldığı gibi, pi’nin değerini milyarlarca basamağa kadar hesaplamak istesin? Pi’nin ondalık basamaklarına karşı bu ilginin kaynağı nedir? Bu, süper bilgisayarların donanım ve yazılımlarının kapasitelerinin ölçülmesinde kullanılır. Hesaplama yöntemleri, yeni düşüncelerin ve kavramların ortaya çıkmasını sağlayabilir. Pi’nin bir düzeni, kalıbı yok mu? Sonsuz çeşitlilikte kalıplar mı içeriyor? Pi’nin içindeki bazı sayılara daha sık mı raslanıyor? Bu sayılar tam da rasgele dağılmış değil mi acaba? Belki de matematikçilerin yüzyıllar boyunca Pi’ye duydukları ilgi ve hayranlık, dağcıları hep daha yükseklere tırmanmaya yönelten güçlü istek ve duygulara benzetilebilir.
Aslında tüm bu soruların yanıtları henüz açık bir şekilde verilebilmiş değildir. Her gün pi ile ilgili yeni bir araştırma yazısı yayınlanmaktadır. İnsanın merak ve tutkusu sürdüğü sürece pi’de yeni bir estetik yön bulma arzusu sonsuza dek devam edecek gibi görünmektedir. Bu yazı, rasgele dizi kavramı çerçevesinde pi’nin ondalık basamaklarını ele almakta, bu ondalık basamakların rasgele dizi tanımına uygunluğunun tartışılması amacını taşımaktadır. Ayrıca, bu ondalık basamaklar kullanılarak nasıl simülasyon yapılacağına dair örnekler verilmiştir.
Evrende olup bitenleri anlama ve anlatma çabası içinde olan insan, ilgilendiği olay ve süreçlerle ilgili çeşitli matematiksel modeller kurar ve bu modeller üzerinde çalışarak gelecekte ne gibi durumlar ortaya çıkabileceğini bilmeye çalışır. Model, gerçek dünyadaki bir sistemin yapı ve işleyişinin, ilgili olduğu bilim sahasının kavram ve kanunlarına bağlı olarak ifade edilmesidir. Model gerçek dünyadaki bir olgunun bir anlatımıdır, temsilidir. Modeller gerçeğin kendileri değildir ve ne kadar karmaşık görünseler de gerçeğin eksik anlatımıdırlar. Kısaca model denilen şey model kurucunun gerçeği “anlayışının” bir ürünüdür. Modellerin geçerliliğini test etmek amacıyla çeşitli deneyler yapılır, bazı durumlarda deney yapmak oldukça güç ve pahalı olabilir. Böyle durumlarda model üzerinde deney yapmak anlamına gelen simülasyon işlemleri yapılır. Simülasyon benzetim, taklit anlamına gelen bir sözcüktür. Günümüzde moda bir sözcük olarak kullanıldır. Modellemede insan aklının en güçlü iki aracı matematik ve istatistiktir. İstatistik özellikle, rasgelelik içeren olguların modellenmesinde ön plana çıkar. Bu durumda “rasgelelik” nedir sorusu önem taşır. “Rasgelelik” tartışmasına burada girilmeyecektir. “Ragelelik” bilim, felsefe ve sanat alanlarında tartışılan başlıca konulardandır. Bu kavramla ilgili geniş bilgiye ulaşmak için kaynakçadaki makalelerden yararlanılabilir.
Ekonometri, Sayısal Çözümleme, Şifreleme, Bilgisayar Programlama, Deneysel Fizik, İstatistik… gibi birçok uygulamalı bilim alanında rasgele sayılar simülasyon aşamasında kullanılır. Simülasyon; rasgelelik içeren olay, sistem ve süreçlerin bilgisayar ortamında model üzerinde deneyinin yapılmasıdır. Son yıllarda simülasyon, özellikle eğitim alanında kullanılan yöntemlerin başında gelmektedir. Simülasyonun temelinde rasgele sayılar yatar. Yapılan simülasyon işleminin gerçek dünyadaki olayı iyi bir şekilde taklit edebilmesi istenir, eğer taklit iyi yapılamıyorsa deney gerçek dünyadaki olayı iyi temsil edemeyecektir. Bu nedenlerle rasgele dizi kavramının uygulama açısından önemi büyüktür. İstatistiksel dağılımlardan gözlem almak için (0,1) aralığında düzgün dağılıma sahip rasgele değişkenlerin çeşitli fonksiyonları kullanılır. Eğer (0,1) aralığındaki düzgün dağılımdan rasgele sayı üretilemiyorsa doğal olarak diğer dağılımlardan da sayı üretmek mümkün olmayacaktır. Bunun için çeşitli üreteçler (fonsiyonel ilişki) kullanılmakta ve çeşitli istatistiksel özellikleri sağlayan üreteçler rasgele sayı üreteçleri olarak kullanılır. Bu sayılar belirli matematiksel kurallara göre üretildiklerinden “sözde rasgele sayı” olarak bilinir. Bilgisayar ortamında bu sayıları üretmek için pek çok yöntem kullanılır. Bu yöntemlerin başında doğrusal eşlenik üreteçleri gelmektedir. Bunlar, x(k+1)=a*x(k)+c (mod m) şeklindedir. x(0) başlangıç, değeri a, c ve m sayıları belirlenerek ardışık olarak sayılar üretilir. Burada önemli olan sayıların birbirini tekrar etmemesi ve istenildiği kadar üretilebilmesidir.
Üretilen bu sayıların bazı istatistiksel özellikleri de sağlaması istenir. Bu şekilde üretilen sayılara “sözde rasgele” sayı denilir. Biz bilgisayarda x(0) başlangıç değerini a, c, m sayılarını bilmediğimizden ve bunlar bazı testleri geçtiğinden rasgele sayı olarak görürüz. Gerçek rasgele sayılar, rasgelelik içeren deneyler sonucunda ya da elektronik araçlar sayesinde üretilir. Kolaylık olsun diye bilgisayarda bu sözde rasgele sayılar kullanılır. Bu rasgele sayıları üretmek ayrı bir uzmanlık alanıdır.
Pi sayısı rasgele sayılar kullanılarak da hesaplanabilir. (x,y) koordinat sisteminde –1≤x≤1 ve –1≤y≤1 karesini ele alalım ve bu bölgeye S diyelim. Yine bu koordinat sistemindeki birim çemberi düşünelim. Birim çemberin oluşturduğu bölgeye de A diyelim. Bu kareye rasgele oklar fırlatalım. Okların birim çemberin içine düşmesi ancak x2+y2≤1 eşitliği sağlandığında gerçekleşir. Karenin alanı 4, çemberin alanı olduğundan rasgele fırlatılan bir okun birim çemberin içine düşmesi olasılığı P(A)=Alan(A)/Alan(S)=/4 olarak bulunur. P(A) değerini yapılan ok atışlarıyla ya da rasgele sayı kullanarak hesaplayabiliriz. Oklar çok kez bu kareye atılır ve çemberin içine düşenler sayılır, buna başarıların sayısı denilirse, toplam başarı sayısının deneme sayısına oranı kullanarak hesaplayabiliriz. Oklar çok kez bu kareye atılır ve çemberin içine düşenler sayılır, buna başarıların sayısı denilirse, toplam başarı sayısının deneme sayısına oranı bize bu olaslıkla ilgili bir fikir verir.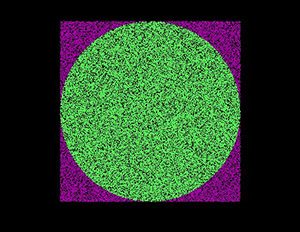
Toplam başarı sayısına m, deneme sayısına n denilirse m/n = /4 eşitliğinden =4 m/n bulunur. Deneme sayısı belli olduğundan sadece m sayısını bulmak işimizi görecektir. Bulunan bu sonuçlardan değeri yaklaşık olarak hesaplanabilir. Buffon’un İğne Problemi; (Doğa bilimci Louis Leclers – Buffon Kontu, 1777)’nin bir geometrik olasılık probleminin çözümü sonucunda ortaya çıkması açısından özellikle ilginçtir. Bu deney herkes tarafından kolayca yapılabilir ve pi için bir tahmin elde edilebilir. Bir düzlem, araları d birim olan paralel çizgilerle ayrılmıştır. Uzunluğu l olan olan bir iğne, bu çizgili yüzeye rasgele düşürülür. Eğer iğne bir çizginin üzerine düşerse iyi atış olarak kabul edilir. İyi atış yapılması olasılığı 2l/d pi dir. l=d=1 alındığında olasılık 2/pi olacaktır. Deney n kez yapılır ve başarıların sayısı m olursa, pi= m/2n olarak hesaplanır. İnternette bu deneyin simülasyonunu yapan sayfalar bulmak mümkündür.
Teorik fizikçi R. Pagels “rasgelelik nedir?” sorusuna yanıt vermeye çalışırken, matematiksel ve fiziksel rasgelelik problemleri arasında ayrım yapmanın önemine değinmiştir. “Matematiksel problem, sayılar veya fonksiyonların rasgele sırasının ne anlama geldiğini tanımlayan bir mantıksal problemdir. Fiziksel rasgelelik problemi gerçek fiziksel olayların rasgelelik konusundaki matematiksel kriterlere uyup uymadığını belirlemektir. Rasgeleliğin matematiksel bir tanımına sahip olana kadar, doğal olayların bir dizisinin gerçekten rasgele olup olmadığını belirleyemeyiz. Bir kere böyle bir tanımımız olunca, o zaman, gerçek olayların böyle bir tanıma karşılık gelip gelmediğini belirleme konulu ek deneysel bir problemimiz olur.”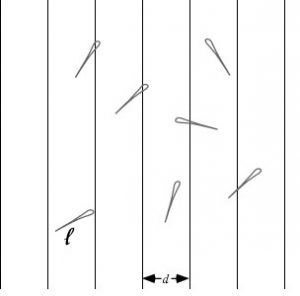
Yazı-Tura atma deneyini düşünelim ve yazıya 0, turaya 1 değerini verelim. 0000000000, 1111111111, 0101010101, 0010100110 dizilerinin ortaya çıkma olasılıkları teorik olarak eşit olmakla birlikte dördüncü dizi hariç diğerlerinin rasgele olmadığı açıktır. İçinde 0’dan 9’a kadar numara verilmiş toplardan oluşan bir kavanozdan iadeli olarak 10 top çekilmesi deneyinde, sırasıyla; 0123456789 ve 0082167489 dizilerinin ortaya çıkması olasılıkları teorik olarak eşit olmasına rağmen yine birinci dizide rasgelelikten kuşku duyulmaktadır.
Elemanları belli bir sayı sisteminin rakamlarından oluşan diziler için rasgele dizi tanımı şu şekilde verilir: Dizideki elemanlar ardışık k’lılar şeklinde ele alındığında bu k’lıların k boyutlu birim küpte dağılışları düzgün ise bu diziye k-düzgün’dür denir. Örneğin, k=1 için b bazına göre rakamlardan oluşan dizinin 1 düzgün olması demek her bir rakamın dizide yer almasının göreli frekansının 1/b’ye yakınsaması demektir. Bir dizisinin kendisi ve tüm alt dizileri her k için k-düzgün ise bu diziye rasgele dizi denir. 1,0,1,0,1,0,1,0,1,0 dizisi 1-düzgün, 0,0,0,0,0,0,0,0,0,0 1-düzgün değil, 1,0,1,0,0,1,1,1,0,1 dizisi 1-düzgün, 2-düzgündür. k = 1, b = 10 bazına göre rakamlardan oluşan dizinin 1-düzgün olması demek her bir rakamın dizide yer almasının göreli frekansının 1/10’a yakınsaması demektir. Simülasyonda sonlu sayıda elemanlı diziler söz konusu olduğunda böyle sonlu elemanlı diziler için rasgelelik nasıl sağlanacaktır? Dizi sonlu elemanlı olduğundan büyük k’lar için k-düzgünlükten hiç söz edilemeyecektir.
Pi sayısının ondalık basamakları üzerinde yapılan çalışmalarda bu sayıların istatistiksel (rasgelelik) testlerin hepsinden geçtiği görülmüştür. Şunu da belirtmek gerekir ki yeni bir istatistiksel test geliştirilebilir ve bu sayılar bu testten kalabilir. Bu ondalık basamaklarda herhangi bir düzen olmadığı görüldüğü halde (bugüne kadar bulunamadı) bir düzen olabileceği varsayımı altında araştırmacılar çalışmalarını sürdürmektedir.
Pi sayısının basamaklarının hesaplanması için birçok yöntem geliştirilmiş ve halen geliştirilmeye devam edilmektedir. Acaba bu basamaklarda istatistiksel bazı özellikler var mıdır? Fazla istatistik bilgisine girmeden bunları gözlemlemeye çalışacağız. sayısının basamakları bir dosyada var olsun (kullanacağımız basamak sayısı 33.554.400, bu yazı ile ilgili programlar, pi hesaplayısı ve diğer dökümanlar leventmodelleme.com adresinden bulunabilir.) Acaba 0,1,2,…,9 sayılarından kaçar tane yer almaktadır. Eğer bunlar düzgün dağılıma sahipseler, yaklaşık olarak aynı oranlarda bulunacaktır. Yani, 0,1,2,…,9 sayılarının her birinden yaklaşık 3.355.440 tane bulunması gerekecektir. Bu sayılardan kaç tane bulunduğu kısa bir bilgisayar programı ile hesaplanabilir. Sonuçların grafiklerini çizip görsel olarak görebiliriz. Buna göre basamak sayıları sırasıyla 3355085 3355565 3356623 3355072 3357257 3356378 3353816 3354630 3354113 3355861 olarak bulunur ve Şekil 1’deki grafik elde edilir. Sonuçtan görüldüğü gibi 0,1,2,…9, rakamlarının sayıları birbirine oldukça yakındır. Bu rakamlar, 1/10 olasılıkla düzgün dağılmış olsalardı herbirinden 3.355.440 tane çıkması beklenirdi. Bu beklenen değerlerle, gözlenen (sayılan) değerler kullanılarak istatistikte Kikare değeri hesaplanabilir (buna bir dağılıma uyum iyiliği testi denir). Bu hesaplandığında gözlenen değerlerin 0,1,2,3,4,5,6,7,8,9 değerlerini 1/10 olasılıkla alan düzgün dağılım olduğu hipotezi kabul edilir. Dosyada bulunan rakamlar yan yana düşünülürse yani, 00, 01,02,…,99 sayılarından kaçar tane yer almaktadır? Bunun için de basit bir bilgisayar programı yazıp sonuçların grafiği çizilirse Şekil 2’deki gibi bir grafik elde edilir. Rakamlar yan yana düşünüldüğünde toplam 33554400/2= 16.777.200 kadar ikili vardır. 00, 01,…,99 sayılarından 16.777.200/100= 167.772 tane olmasını bekleriz. Şekilden görüldüğü gibi ikililerin sayısı 167.772 civarında yer almaktadır. Buradaki beklentimizin nedeni de 00,01,…99 sayılarının dağılımının 1/100 olasılıkla düzgün dağılım olmasıdır. Yine benzer şekilde Kikare hipotez testi yapılmış ve bunların düzgün dağılıma sahip olduğu görülmüştür.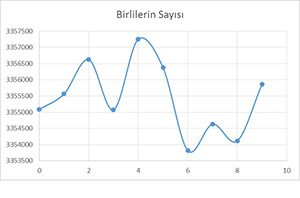

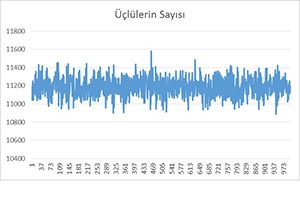

Benzer şekilde üçlülerin toplam sayısı 11.184.800 ve herbir üçlü için beklenilen değer 11.184 iken dörtlülerin sayısı 8.388.600 ve beklenen değer 838 dir (Şekil 3 ve 4). Bunlar için de hipotez testi yapılmış ve düzgün dağılıma sahip olduğu görülmüştür. Böylece 1-2-3-4 düzgünlük sağlanmıştır. Aklımıza acaba daha fazla sayıda düzgünlük, örneğin, 100, 1000 düzgünlük istatistiksel olarak sağlanıyor mu sorusu gelebilir. Bunun için elimizdeki 33.554.400 adet basamak yetmeyecek, milyarlarca trilyonlarca basamağın hesaplanması gerekecektir. Bu kadar basamağı hesaplamak daha çok matematik ile birlikte bilgisayar donanımı ve yazılımı gerektirir.
Bu basamakları hesaplamak hem matematiksel bilgiyi hem de iyi derecede algoritma tasarımını gerektirir ve bu algoritmalar zaman da yeni geliştirilen bilgisayarların hızlarını test etmek amacıyla kullanılır. Pi ’nin milyarlarca basamağı cd’lere kaydedilerek bazı durumlarda simülasyon çalışmalarında doğal rasgele sayı olarak
kullanılır. Şimdiye kadar bu basamaklar rasgelelikle ilgili tüm istatistik testlerinden geçmiştir.
Şimdi Pi sayısının basamaklarını kullanarak bir simülasyon çalışması yapalım. Bilgisayardaki rasgele sayı üreteçlerini kullanmadan aşağıda tarif edildiği gibi gerçekleştirilebilir. Belirli bir başlangıç noktasında 1000 tane çekirge bulunsun ve her biri eşit olasılıkla kuzey-güney- doğu-batı yönlerine doğru 1 birim uzunlukta hareket etsin. Sırası gelen çekirge bu yönlerden birisini seçsin ve hareket etsin. 1000 tanesi 1 birim hareket ettikten sonra bulundukları yerden yine eşit olasılıklabu rasgele hareketi sürdürsün. Çekirgelerin yön seçimi ile ilgili bu rasgele hareketten simülasyon ile nasıl gözlem alınacaktır? Pi sayısının basamaklarının 2 düzgünlük testinden geçtiğini biliyoruz. O halde bu basamakları kullanrak bu yön seçimi için bir kural koyulabilir. 00,01,…,24 için kuzey, 25,26,…,49 için güney, 50,51,…,74 için doğu, 75,76,…,99 için batı yönleri seçilebilir. Çekirgeler buna göre zıpladıklarında gittikleri yerler işaretlendiğinde aşağıdaki gibi güzel bir görüntü ortaya çıkar. Bu küçük bir bilgisayar programı ile yapılabilir ve animasyon şeklinde görülebilir. Eşit olasılıkla hareket etmeselerdi sayısının basamakları kullanılamayacaktı. Sonuç olarak, çekirgeler bir tarlanın ortasına konulur ve eşit olasılık ile rasgele hareket ederlerse tarladaki ürünün tamamını belirli bir süre sonunda tüketeceklerdir.
Bunun gibi değişik sonuçları görmek için değişik düşünceler geliştirilip farklı araştırmalar yapılabilir. Pi sayısının basamaklarının resmi çizilebilir, müziği yapılabilir.
1415926535897932384626433832795028841971693993751058 20974944592307816406286208998628 basamaklarını tekrar ele alalım. 1’den bir adım sonra 1’le karşılaşılır, buna başarı diyelim. Başarı olasılığı 1/10 olan bir basketçinin ilk başarıyı elde edene kadar yaptığı atışların sayısı olarak görülebilir. Acaba bu basketçinin ilk başarıyı elde edene kadar yaptığı atışların ortalaması ne olur? Örneğin bu başarıdan 33 atıştan sonra tekrar basket atacak, bundan sonra da 18 kez atış yapacaktır. Bu düşünceyi genişletmek olanaklıdır. Bunları gözle saymak oldukça güçtür; basit küçük bir bilgisayar programı yapılarak ilk başarıyı elde edene kadar yapılan atışların sayısının dağılımı ortaya çıkarılabilir. Diğer 0,2,…,9 rakamları için de benzer adım sayımları yapılabilir. Dökümanlardan elde edeceğiniz Pi sayısının basamaklarını kullanarak çeşitli özellikler keşfedebilir ve yüzünüzde güzel gülümsemeler oluşturabilirsiniz. Bu, sayılarla uğraşmanın, sadece beyninizde değil, bedeninizdeki yansımanın da bir görüntüsü olacaktır.
Kaynaklar
1) Blatner, D. (2003), Coşkusu, Tübitak Yay.
2) Pagels, H. R. (1992), Kozmik Kod, Doğanın Dili/Kuantum Fiziği, Sarmal Yay.
3) Morgan, B. J. T. (1992), Elements of Simulation, Chapman and Hall.
4) Deak, I. (1990), Random Number Generators and Simulation, Akademiai Kiado.
5) Dodge, Y. (1996), A Natural Random Number Generator, International Statistical Review, 329-344.
6) Jaditz, T. (2000), Are the Digits of an Independent and Identically Distributed Sequence?, The American Statistician, Vol.54, No.1, 12-16.
7) Lange, L. J. (1999), An elegant Continued Fraction for , The American Mathematical Mountly, Vol.106, N.5, 456-458.
8) Osler, T. J. (1999), The Union of Vieta’s and Wallis’s Product for Pi, The American Mathematical Mountly, Vol.106, N.8, 774-776.
9) Öztürk, F., Özbek, L. (2015). Matematiksel Modelleme ve Simülasyon, Pigeon Yay.
10) Özbek, L. (2016), Reflections and Comments on Randomness, Econometrics Letters Volume (3), pp. 28-33.
11) Özbek, L., Babacan, E. K. ve Başkır B. (2013), Algoritma tasarımına giriş, Matematiksel ve İstatistiksel Uygulamalar, Gazi Yay.
12) Bailey, D. H., Borwein, JH ve Ploufle, S. (1996), The Quest for pi, The Mathematical Intelligencer.
13) Borwein, P. (2000), The amazing number , NAW 5/1, nr.3, 42-46.
14) Ganz, R. E. (2014), The Decimal Expansion of π Is Not Statistically Random, Experimental Mathematics, 23:99–104, 2014
15) Bailey, D. H., M. Borwein, JH. ve diğ. (2012), An Empirical Approach to the Normality of π, Experimental Mathematics, 21(4):375–384.
16) Ganz, R. E. (2017), Reply to “Reproducibility in Computational Science: A Case Study: Randomness of the Digits of Pi”, Experimental Mathematics, Vol. 26, No:3, 306-307.
17) Bailey, D. H., M. Borwein, J. H. Ve diğ. (2017), Reproducibility in Computational Science: A Case Study: Randomness of the Digits of Pi, Experimental Mathematics, Vol. 26, No:3, 298-305.
18) P. Borwein, kişisel web sayfası http://www.cecm.sfu.ca/personal/pborwein.










