Kuantum sonrası (Post-quantum) kriptografi (şifreleme) klasik kriptografinin bir evrimidir, zor matematiksel problemleri kullanır fakat tamamen kuantum bilgisayarların saldırısına karşı oluşturulmuş şifreleme yöntemidir. Eğer bugünün kriptografi protokolü başarısız olsaydı çevrimiçi bağlantıları(özel mesajlar göndermek, finansal işlemleri korumak, verileri doğrulamak) korumak imkansız olurdu. Herkes her şeye ulaşabilir, herkes herkesmiş gibi davranabilir, dijital ekonomi yıkılabilirdi.
2017 yılında ABD hükümetinin Ulusal Standartlar ve Teknoloji Enstitüsü “Kuantum sonrası” kriptografiyi elde etmenin en iyi yollarını bulmak için uluslararası bir rekabet başlattı. Geçen ay, ajans ilk kazanan grubunu seçti, bazı revizyonlarla kuantum kalkanı olarak dağıtılacak dört protokoldü. Ayrıca 4 fazladan aday hala incelenmekte. 30 Temmuz’da, bir çift araştırmacı bir dizüstü bilgisayarda, sadece 1 saate o adaylardan birini kırdıklarını açıkladı. Yeni Zelanda’daki Auckland Üniversitesi’nde matematikçi ve bilgisayar bilimcisi olan Steven Galbraith, “Çok dramatik ve güçlü bir saldırı… oldukça şok edici oldu” dedi.
Saldırının altında yatan matematik şaşırtıcı olan tek şey değildi, ama NIST yarışmasındaki şemalarından farklı bir şekilde çalışan bir şifreleme protokolünü elemek kuantum sonrası kriptografinin çeşitliliğini azalttı. Sonuçlar kuantum sonrası kriptografiyi sarsılmış ve cesaretsiz bıraktı. Sarsıldı çünkü bu saldırı aniden dijital çelik bir kapı gibi görünen şeyi ıslak bir gazeteye çevirdi.
Eğriler arasında gizli yürüyüşler
IBM araştırmacısı Jao ve De Feo birbirine benzeyen ve iyi bilinen protokollerden oldukça belirgin olan şifreleme sistemi için bir şans gördü. Onların ‘Supersingular Isogeny Diffie-Hellman Protokolü (SIDH) olarak adlandırılan şemaları, eliptik eğrilerle çalıştı.-bugün klasik şifrelemenin en yaygın çeşidinde kullanılan matematiksel objeler ile aynı.- Ama tamamen farklı bir şekilde kullanıldı. NIST’in göz önünde bulundurduğu en kompakt şemaydı. Jao, “matematiksel olarak gerçekten zarif” dedi. “O zaman, güzel bir fikir gibi görünüyordu.”

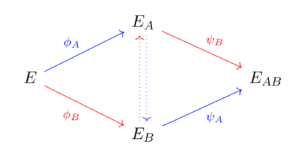
Temel olarak Bob ve Alice aynı eğri üzerinden yürümeye (E0) başlar ve sonra eğrilerden rastgele bir şekilde uzaklaşırlar. Bu EA (Alice’in Eğrisi) ve EB’yi (Bob’un Eğrisi)’ni oluşturur. Bob Alice’e eğrisini gönderir ve Alice de Bob’a eğrisini gönderir. Alice daha sonra EB’den, Bob ise EA’dan tekrar rastgele yürüyüşe başlar. Sonunda yeni bir gizli eğriyle buluşurlar. Bu sadece kendileri tarafından bilinen bir eğri olacak ve hem Bob’un hem de Alice’in rastgele yürüyüşünü bilmedikçe başka hiç kimse bu eğriyi bilemeyeceğinden, bunu yeni bir anahtar oluşturmak için kullanabilirler. Saldırgan, Alice ve Bob’un birbirine gönderdiği ara noktaları görse bile, Alice’in ya da Bob’un gizli yürüyüşünü bilmiyorlar, yani süreçte final noktasını çözemiyorlar.
Örnek:
Diyelim ki Bob ve Alice y=4x+3 noktasından başlıyorlar
Bob x+2 kadar yürüyor.
yB = 4 (x+2) + 3 = 4x + 11
Alice x-3 kadar yürüyor.
yA = 4 (x-3) + 3 = 4x-9
Eğer bob Alice’in yürüdüğü yerden x+2 kadar yürüseydi
kB = 4 (x+2) — 9 = 4x -1
Eğer Alice Bob’un yürüdüğü yerden x-3 kadar yürüseydi
kA = 4 (x-3) + 11 = 4x -1
ve böylece Bob ve Alice aynı lineer denkleme sahiptir ve eğer x değerini alırlarsa, aynı anahtarla sonuçlanırlar.
Eski matematikte yeni bir büküm
Thomas Decru SIDH’ı kırmak için yola çıkmadı. Onu başka bir şifrelemeyi geliştirme metodunu genelleştirmek için inşa etmeye çalışıyordu. İşe yaramadı ama bir fikir ortaya çıkardı:
Onun yaklaşımı SIDH’a saldırmak için faydalı olabilirdi. Böylece Belçika’daki Leuven Katolik Üniversitesi’ndeki meslektaşı ve eski doktora danışmanlarından biri olan Wouter Castryck’e yaklaştı ve ikisi ilgili literatüre daldı.
Matematikçi Ernst Kani tarafından 1997’de yayınlanan bir makaleye rastladılar. Castryck, “neredeyse hemen SIDH için geçerli olan” bir teorem olduğunu söyledi. “Sanırım bir kez fark ettiğimizde… saldırı bir veya iki gün içinde oldukça hızlı geldi.” Sonunda, Alice’in gizli yürüyüşünü iyileştirmek için (ve dolayısıyla paylaşılan anahtarı) Castryck ve Decru iki eliptik eğrinin çarpımını incelediler.- Alice’in başlangıç eğrisi ve Bob’a herkese açık bir şekilde gönderdiği eğri. Bu kombinasyon değişmeli yüzey adı verilen bir çeşit yüzey oluşturdu. Sonrasında bu değişmeli yüzeyi kullandılar, Kanii’nin teorisi (değişen yüzeyleri eliptik eğrilerle ilişkilendirir) ve Alice’in Bob’a verdiği ekstra bilgi Alice’in attığı her adımı ortaya çıkardı.
Jao, “Neredeyse belirli değişmeli yüzeylere kilitlenmenizi sağlayan bir hedef arama sinyali gibi.” Dedi. “Ve bu sinyal size doğru (gizli yürüyüşü) bulmak için bir sonraki adımı atmanız gereken yolun bu olduğunu söylüyor.” Bu da onları direkt Alice ve Bob’un ortak anahtarına götürdü. Jao ayrıca, “daha basit nesneler hakkında sonuçlar elde etmek için daha karmaşık nesnelere gitmek çok beklenmedik bir yaklaşım” dedi. Meta AI Research‘teki bir matematikçi ve kriptograf olan Kristin Lauter, sadece Isogeny tabanlı şifrelemenin geliştirilmesine yardımcı olmakla kalmayıp, aynı zamanda Abelian yüzeylerinde de çalışan Kristin Lauter, “Bu tekniğin kullanıldığını görmek beni çok heyecanlandırdı” dedi. “Bunu kırmanın bir yolu olarak düşünmediğim için bana utanç duyuyorum.” diye de ekledi.
Castryck ve Decru’nun saldırısı, SIDH protokolünün en düşük güvenlikli sürümünü 62 dakikada ve en yüksek güvenlik düzeyini bir günden kısa sürede kırdı. Ardından, kısa bir süre sonra, başka bir uzman, düşük güvenlikli sürümü kırmak sadece 10 dakika ve yüksek güvenlikli sürümü kırmak için birkaç saat sürecek şekilde saldırıyı değiştirdi. Son birkaç hafta içinde yayınlanan daha genel saldırılar, SIDH’nin kurtarılmasını pek olası kılmıyor. “Bu özel bir duyguydu,” dedi Castik, acı tatlı olsa da. “En sevdiğimiz sistemlerden birini öldürdük.”
Dönüm noktası
Castryck ve Decru’nun saldırısı, SIDH protokolünün en düşük güvenlikli sürümünü 62 dakikada ve en yüksek güvenlik düzeyini bir günden kısa sürede kırdı. Ardından, kısa bir süre sonra, başka bir uzman, düşük güvenlikli sürümü kırmak sadece 10 dakika ve yüksek güvenlikli sürümü kırmak için birkaç saat sürecek şekilde saldırıyı değiştirdi. Son birkaç hafta içinde yayınlanan daha genel saldırılar, SIDH’nin kurtarılmasını pek olası kılmıyor. “Bu özel bir duyguydu,” dedi Castik, acı tatlı olsa da. “En sevdiğimiz sistemlerden birini öldürdük.”
Bu yüzden NIST’ler gibi yarışmalar bu kadar önemli. NIST yarışmasının önceki turunda, IBM’de bir kriptograf olan Ward Beullens, bir hafta sonu Rainbow isimli bir planı kıran bir saldırı oluşturdu. CireCk ve DeSru gibi, saldırısını ancak altında yatan matematiksel problemi farklı bir açıdan izledikten sonra sahne alabildi. Ve Sidh’e yapılan saldırı gibi, bu, önerilen en çok kuantum sonrası protokollerden farklı matematiğe dayanan bir sistemi kırdı.
PQShield başlangıcında kriptograf olan Thomas Prest, “Son saldırılar bir dönüm noktasıydı” dedi. Kuantum sonrası kriptografinin ne kadar zor olduğunu ve çeşitli sistemlerin güvenliğini incelemenin ne kadar analiz gerekebileceğini vurguluyorlar. “Matematiksel bir nesnenin bir perspektifte bariz bir yapısı olmayabilir ve diğerinde sömürülebilir bir yapıya sahip olabilir” dedi. “Zor kısım, yeni bir doğru bakış açısını belirlemektir.”
Kaynaklar:










