Kuantum fiziğine giriş

Çevremizde gördüğümüz hemen her şeyin açıklaması ancak kuantum kuramı ile mümkün. Kuantum kuramı olmasa, Güneş’in neden parladığı, gökyüzünün neden mavi olduğu, neden masanın üstünde duran kitapların yere düşmediği gibi birçok olayı açıklayamayız. Ancak kuantum fiziğinin yasaları deneyleri doğru bir şekilde öngörse de, doğanın neden böyle davrandığını bilmiyoruz. Evet, elimizde çok harika bir kuram var. Ancak felsefi arka planı hâlâ eksik. Daha doğrusu kuantum fiziği bizim makro-dünyada şekillenmiş olan felsefemizi değiştirmemiz gerektiğini zorluyor.

Kuantum nedir?

Kökeni Latince olan kuantumun sözlük anlamı pakettir; öbeklenme anlamına gelir. Gündelik yaşamda çok alışkın olduğumuz bir kavramdır: çakıl taşları, elmalar, armutlar, ekmek somunlar vs hep öbekler halindedir. Ancak fizikte bu öbeklilik çok derin anlamlara yol açar: enerjinin öbekli olması, hatta uzay-zamanın öbeklenmesi, atom çekirdeği etrafında bulunan elektron yörüngelerinin öbekli olması vb gibi hiç alışkın olmadığımız olgular bulunur. İçinde yaşadığımız makro-dünyada her şey öbekli değildir. Örneğin dünya etrafında bir uyduyu istediğimiz yörüngeye oturtabiliriz. Bir yokuşta istediğimiz noktada dururuz. Oysa kuantum fiziğinin betimlediği mikro-dünyada her şey öbeklidir. Enerji paketler halinde gelir, elektron yörüngeleri ancak belli değerlerde olabilir vs. Adı üstünde, kuantum dünyası öbeklilik (ya da kesiklilik diyebiliriz) dünyasıdır. Ayrıca kuantum hem sıfat hem de isim olarak kullanılır. Kuantum fiziği ve kuantum sıçramalarından söz ettiğimiz gibi, enerji kuantumu veya ışığın kuantumu da deriz. İsmin çoğulu ise kuanta’dır.

Aslında fizik yasaları hem makro-dünyada hem mikro-dünyada aynıdır; ancak farklı boyutlarda, farklı kuvvetler diğerlerine göre daha etkin olur. Örneğin içi su dolu bir kovayı ters çevirdiğinizde, kütleçekim kuvveti nedeniyle içindeki su dökülür. Bu bizim alışkın olduğumuz makro-dünya boyutudur. Öte yandan kovanın içinde birkaç damla su kalır. Kütleçekim kuvveti bu birkaç damlayı çekemez, çünkü artık daha küçük boyutlarda başka kuvvetler etkin olmuştur. Su molekülleri arasındaki Van der Waals kuvvetleri kütleçekimden daha baskındır. O nedenle damlalar kovanın dibine yapışıp kalır. Daha da küçük boyutlara, atom ve atom-altı boyutlara inersek, bu kez tamamen başka kuvvetler devreye girer. Atom boyutlarındaki kadar küçük mesafelerde elektromanyetik, zayıf ve yeğin (nükleer) kuvvetler hakimdir ve bu boyutlarda doğa yasaları kuantum mekaniği ile betimlenir. Bu üç kuvvet (elektromanyetik, zayıf ve yeğin kuvvetler), kütleçekim kuvveti ile birlikte evrendeki dört temel kuvveti meydana getirir. Kütleçekim kuvveti diğer üç kuvvete göre çok zayıf kaldığı için atom-altı boyutlarda sadece bu üç kuvvet hâkimdir.

Örneğin hidrojen atomu, yaklaşık bir çapa sahiptir; Heisenberg belirsizlik ilkesi yüzünden hatlar keskin değildir. Hidrojen atomunun boyutları yaklaşık olarak metrenin on milyarda birinden daha küçük olamaz. Bu atomun taban durumu dediğimiz büyüklüğüdür ve bununla bağlantılı olarak da belli bir enerji, onun taban durumu enerjisidir. Hidrojen atomu daha az bir enerjiye sahip olamaz. Dolayısıyla temel hidrojen atomu öbeği bu taban durumu enerjisidir ve her hidrojen atomu tam olarak aynı boyuta ve aynı enerjiye sahiptir. Atomlar daha büyük ve daha enerjik hale getirilebilir, ancak bu da sadece kesikli kuantum artışlarıyla gerçekleşir. Böylesi daha büyük boyutlara ve daha yüksek enerji durumlara uyarılmış durumlar denir.

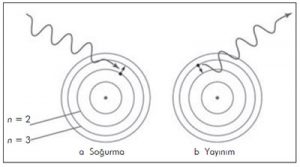Üzerine gelen fotonu (ışık parçacığı) soğurup uyarılan bir atom, bir ışık fotonu saldığı ve enerjisini daha yüksek bir değerden daha düşük bir değere düşürdüğü zaman, bir kuantum sıçraması yapıyor demektir. Atomdan salınan foton da bir kuantumdur, yani bir ışık öbeğidir. Kuantum dünyasında sadece nesneler değil, nesnelerin belli özellikleri de kesikli kuantum öbekleri biçiminde karşımıza çıkar. Örneğin birim elektrik yükü, bir proton (veya negatif yüklü bir elektron) tarafından taşınan miktardır. Elektrik yükünün kesirli bir kuantum birimi olması gibi bir şey de mümkün değildir. Evrendeki her elektrik yükü, proton veya elektron yükünün tam sayı katıdır. Temel parçacıklar içerisindeki kuarklar 1/3 ve 2/3 birim yükler taşısalar da, bunlar her zaman öyle bir biçimde birleşirler ki, tüm gözlenen veya ölçümlenmiş yükler proton veya elektron yüklerin tamsayısıdır.

Günlük yaşamda bu öbekliliği hissetmeyiz. Örneğin suyun H₂O moleküllerinden oluştuğunu biliriz, ancak bu bizim için önem taşımaz: Aynı şekilde, suyun sıcaklığını, akışkanlığını, basıncını, ağdalılığını veya türbülansını ölçen bir fizikçi için de bu öbeklilik önemli değildir. Klasik fizik dediğimiz, kuantum öncesi fizik o nedenle daha büyük boyutların fiziğidir. O boyutlarda artık öbeklilik önem taşımaz. Tek bir su molekülünü ele aldığımızda ise işler farklılaşır. Klasik fizik bunu inceleyemez. Tek bir su molekülü bir kuantum varlıktır ve anlaşılması ancak kuantum fiziğinin yardımıyla mümkün olabilir. Yine bu geçişin, mikro-dünyadan makro-dünyaya geçişin nasıl gerçekleştiğini bilmiyoruz. Bu fiziğin en büyük gizemlerinden biridir.

Öte yandan, bu mikro-dünya/makro-dünya ikiliğinin kuantum etkilerinin gündelik dünyamızda kendisini doğrudan hissettirdiği az sayıda olgu vardır. Bunların en popüleri süperiletkenliktir. Süperiletken malzemelerde, çok düşük sıcaklıkta elektronlar bir dirençle karşılaşmadan hareket ederler. Atomların ve moleküllerin çok daha küçük ölçekli dünyasında elektronların sürtünmesiz hareketi sıradan bir olaydır. Çünkü kuantum yasaları sayesinde enerjileri minimum bir değerin altına düşmez. Ama makro-dünyada, örneğin bir kablo içinde elektronlar normalde dirençle karşılaşırlar ve elektrik potansiyeli gibi bir dış güçle itilmiyorlarsa akışları durur. Oysa süperiletkenlerde, elektronlar itilmeden durmaksızın yol alabilirler. İşte bu kuantum fiziğinin izin verdiği sürtünmesiz hareketin makro-dünyada kendisini göstermesidir.

Kuantum fiziğinin alıştığımız dünyadan farklı yanları bununla kalmaz. Sağduyuya aykırı gelen pek çok tuhaf yanı vardır kuantumun. Ama bunları incelemeden önce biraz fizik tarihine bakalım.

Her şey ışıkla başladı

Işığın doğasıyla ilgili tartışmalar neredeyse iki yüzyıldır devam etmekteydi. Newton ışığın taneciklerden oluştuğunu öne sürmüştü ama kütleçekim kuramını kullanarak girişim, kırınım, yansıma vb gibi ışık olgularını açıklamakta pek başarılı olamamıştı. 19. yüzyılın başlarında, Newtoncı ışık görüşü terk edilmeye başlandı. İngiliz biliminsanı Thomas Young’ın (1773-1829) çift-yarık deneyi bunda anahtar rol oynadı.

Young’ın deneyinde, önce karanlık bir odadaki ışık demeti, bir levhadaki dar bir yarıktan geçirilerek ince bir demet elde edilir. Daha sonra levhanın diğer tarafına geçen ışık, ikinci bir levhadaki iki paralel yarıktan geçirilir ve beyaz bir levha üzerine düşürülür. Eğer ışık taneciklerden oluşsaydı, beyaz levha üzerindeki görüntü ışık parçacıklarının yığılmasıyla giderek solan iki ışık çizgisi olmalıydı. Oysa Young’ın gördüğü görüntü, son levha üzerinde ışıklı ve gölgeli çok daha karmaşık bir görüntüydü. Buna girişim çizgileri denir. Tıpkı durgun bir suya atılan iki taşın yarattığı dalgaların birbirlerini yok etmesi ve güçlendirmesiyle ortaya çıkan karmaşık girişim çizgileri gibi görüntüler elde eden Young, ışığın dalga doğasını ispatlamış oldu.

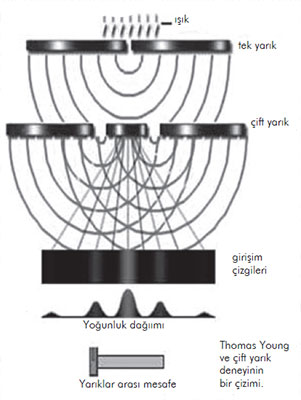
Young bu deneyleri 19. yüzyılın ilk on yılında yürütüp yayımlamışsa da, Fresnel’in tamamlayıcı çalışmalarına rağmen 1820’li yıllara hatta daha sonralarına kadar ışığın dalga kuramı kabul edilmemişti. Kuramın tam olarak oturması daha da uzun bir süre almıştır. Işığın doğası hakkındaki bulmaca, Young ve Fresnel’in çalışmalarıyla hiç ilgisi olmayan incelemelerle, elektromanyetizmayla, tamamen çözülebilmiştir.

18. yüzyılın başlarında elektromanyetizma bilinmiyor, elektrik ve manyetizma iki farklı konu olarak inceleniyordu. Bu iki konuyu bir araya getiren İngiliz fizikçi Michael Faraday (1791-1867) elektrik akımının nasıl manyetik bir alan üretebileceğini ortaya koyarak, farkında olmadan ışığın doğasını açıklamaya giden yolda en önemli katkılardan birini yapmıştır. 1860’ta Faraday’ı tamamlayan İskoç fizikçi James Clerk Maxwell (1831-1879) elektromanyetizmanın tam bir kuramını geliştirerek, ışığın aslında elektromanyetik dalga olduğunu gösterdi. Maxwell 1861 ve 1862’de yayımladığı dört bilimsel çalışmayla elektromanyetik dalgaların yayınımının matematiksel bir açıklamasını yaptı. Denklemlerde, elektromanyetik dalgaların hareketinin hızlarını içeren bir sayı vardı. 1850’lerde yapılan deneylerle ölçülen bu sayının, kesin olarak ışık hızına eşit olması Maxwell’i doğruluyordu. Böylelikle uzun yıllardır süre giden tartışma sonuçlanmış görünüyordu: Işık bir dalga gibi yayılıyordu. Oysa 50 yıl kadar sonra ışığın parçacık kuramı tekrar sahneye çıkacaktı.

Kendilerine rağmen devrimciler: Planck ve Einstein

Kuantum kavramlarının sahne almaya başlaması, 20. yüzyılın hemen başıdır. Alman fizikçi Max Planck (1858-1947) 1900 yılında elektromanyetik ışınımların doğasıyla ilgili temel bir sorunu çözdüğünü duyurdu. Sorun kara cisim ışımasının açıklanmasıydı.

Kara cisim, üstüne düşen ışık dahil her türlü elektromanyetik ışınımı soğuran bir cisimdir. Ama genel olarak kara cisim ışınımı (ya da kovuk ışınımı) ısıtılan bir cismin yaydığı ışınım olarak bilinir. Laboratuvarda oluşturulabilecek en uygun kara cisim, üzerinde küçük bir delik bulunan yalıtılmış büyük bir kutudur. Delikten içeri giren ışık içerdeki kovuğun duvarlarına çarpıp yansıyarak dolanır ve kutuyu ısıtır. Kovuktan geçip dışarı çıkan kovuk ışınımının ‘tayfı’ sadece kovuğun sıcaklığına bağlıdır. 1850’lerden beri incelenen kara cisim ışınımı etrafımızdaki pek çok olayda görülür. Örneğin, yaklaşık 6000 ºC yüzey sıcaklığına sahip güneşten gelen ışınım bir kara cisim ışınımıdır. Deneysel olarak ölçülebilen bu ışınımın dalga boylarına göre yoğunluk tayfı çıkarılmıştı. Ama 19. yüzyılın sonlarında fizikçilerin çözemediği bilmece, bu kara cisim ışımasının düşük dalga boylarında neden sonsuz parlaklığa ulaşmadığıydı. Diğer bir deyişle, o zamanki fizik kuramları kara cisim tayfını açıklayamıyordu.

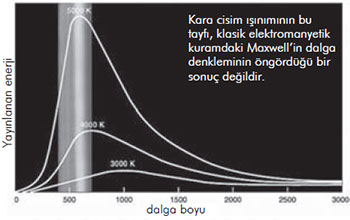
Kara cisim ışınımının bu tayfı, klasik elektromanyetik kuramdaki Maxwell’in dalga denkleminin öngördüğü bir sonuç değildir.

Klasik olarak yayınlanan enerji miktarının, dalga boyunun tersiyle orantılı olması gerektiğinden, elektromanyetik dalgalar (diğer dalgalar gibi) incelenirse, kısa dalga boylarında enerji yayınımının daha kolay olacağı görülür. Dolayısıyla bir kara cisim, hesaplamalara göre, daha kısa dalga boylarında daha büyük enerji yayınlamalıdır. Bu sonuç “morötesi felaketi” olarak bilinir. Felakete uğrayan kuramdır, çünkü hesaplamaların arka planında bazı yanlışlar bulunmalıdır ama nedir bu yanlışlar? İşte kuantum devrimini başlatan şey bu soruya verilen yanıttı.

Planck, kara cisim ışımasını kuramsal olarak açıklayabilmek için ışığın paketler, daha sonraki adıyla kuantalar halinde gelmesi gerektiğini fark etti. Işığın enerjisinin kesikli olduğu varsayılsa, kara cisim tayfı açıklanıyordu. Mor ötesi felaket ortadan kalkıyor, gözlem ile kuram uyum içinde oluyordu. Ancak yine de Planck ışığın bir dalga olduğuna ve ancak atomlar tarafından belirli miktarlarda soğurulabilir ya da yayımlanabilir olduğuna inanıyordu. Fotonlar olarak da bilinen ışık kuantalarının açıklanması beş yıl sonra 1905’te Albert Einstein (1879-1955) tarafından yapılacaktı. 1900’de Max Planck, enerji paketlerine ‘enerji elementleri’ adını verdi ve bunların ışığın frekansına

E = hv

denklemiyle bağlı olduklarını ortaya koydu. Burada E bir ‘element’in enerjisini, v (nü) harfi dalganın frekansını, h ise Planck sabiti olarak bilinen basit bir sayıyı gösterir. Dalganın frekansı, ışık hızı bölü dalga boyu olduğundan, yüksek frekans kısa dalga boyu anlamı taşır.

Kara cisim eğrisinin açıklanmış olmasına karşın bu bir anda kuantum fiziğini başlatmadı. Kesikli enerji fikri çok yeniydi ve bunun ışığın doğasıyla ilgili olduğunu Einstein’dan başka hiç kimse anlamadı. Planck’ın kendisi bile bu bilgiyle ne yapacağını bilmiyordu. Planck’ın buluşunu yaptığı 1900 yılında ETH olarak bilinen İsviçre Teknik Üniversitesi’nden mezun olan Einstein, başarılı bir öğrenci değildi; derslere devam etmeyip sadece istediği konuları araştırıyordu. Sınıfın en düşük not ortalamasıyla mezun oldu ve ETH’de doktora yapma hedefini gerçekleştiremedi; Bern patent ofisinde çalışmaya başladı. Ama 1905 yılında orada çalışırken, şaşırtıcı düzeyde bilimsel çalışmalar yayımlamayı başardı: Bir doktora tezi, özel görelilik kuramı ve kendisinin ‘çok devrimci’ olarak nitelendirdiği bir çalışma. Bu, fotoelektrik etkisi adıyla bilinen bir olgunun açıklamasıydı. Einstein bu çalışmada, fotoelektrik etkiyi ışık kuantalarını gerçek bir olgu olarak ele alıp fotonların gerçekte parçacık olduklarını gösterdi.

Günümüzde güneş pillerinde de kullanılan fotoelektrik etkisi Alman fizikçi Philipp Lenard’ın (1862-1947) 1899 yılında ortaya çıkardığı bir olgudur. Lenard, vakum altında bir metal yüzeye düşürülen morötesi ışınımın ürettiği, bugün elektronlar olarak bilinen katot ışınımı üzerine araştırmalar yapıyordu ve üretilen elektronların enerjilerinin yüzeye düşen ışığın parlaklığına değil, ışığın frekansına bağlı olduğunu bulmuştu. Oysa zayıf bir ışığın enerjisi parlak bir ışığın enerjisinden daha küçük olmalıydı; bu yüzden de zayıf bir ışık demeti, daha düşük enerjili elektronlar üretmeliydi. O tarihlerde bilindiği kadarıyla ışığın frekansının bununla ilgisi olmamalıydı. İşte Einstein’ın fotoelektrik etkiyi açıklaması gerçek anlamda kuantum devrimini başlatır: Eğer n frekansıyla titreşen elektromanyetik ışınım, her biri hn enerjisine sahip parçacıkların bir demetiyse, şimdi foton dediğimiz bu parçacıklardan biri metalden aynı miktardaki enerjiye sahip bir elektronu fırlatacaktır. Işığın parlaklığı azaltılınca fotonların sayısı azalır ama belirli bir frekansta, her foton aynı enerjiye sahiptir. Einstein ışık kuantasının bütün enerjisini tek bir elektrona geçirdiğini söyleyerek, ışığın aslında bir parçacık olduğu fikrini ortaya attı. Enerji kuantaları tam sayılı birimler halinde soğuruluyor veya yayınlanıyordu. Ama1905 yılında bu iddiayı desteklemeye yetecek duyarlı aletler yoktu; Einstein’ın kuantum fiziği hakkındaki görüşleri on yıl boyunca dikkate alınmadı.

Einstein’ın bu görüşlerini beğenmeyen ve onları yanlışlamaya uğraşan Amerikalı deneyci Robert Millikan, 1949’da Review of Modern Physics dergisinde yazdığı bir makalesinde “Einstein’in 1905 denklemini deneyerek yaşamımın on yılını harcadım, bütün beklentilerim dışında, anlamsızlığına karşın denklemin gerçekten doğru olduğunu belirtiyorum” der. Yine de Millikan’ın deneyleri Planck Sabiti’nin doğru olarak ölçülmesini ve onun gerçek bir anlamı olduğunun gösterilmesini sağlamıştı. Sonuçta 1918 Nobel fizik ödülü Planck’a, 1921 fizik ödülüyse Einstein’a verildi.

Bu arada kuantum fiziğindeki ilerlemeler büyük bir ivme kazanmıştı. Rutherford, atomların pozitif yüklü bir çekirdeğe sahip olduğunu 1911 yılında açıklamıştı. Ama ortada yine bir sorun vardı. Eğer elektronlar negatif yüklüyse ve atomun çekirdeği de pozitif yüklüyse, karşıt yükler birbirlerini çektikleri için, bütün elektronların çekirdeğin üstüne düşmeleri gerekirdi. Bu sorunun yanıtını da kuantum kuramının kurucularından biri kabul edilen Danimarkalı fizikçi Niels Bohr (1885-1962) verdi: Açısal momentum da kuantize durumdaydı. Diğer bir deyişle, elektronlar atom etrafında ancak kesikli yörüngelerde bulunabilirdi.

Bohr, Planck kuantalarının belirli büyüklükteki enerjileri yayabileceğini veya soğurabileceğini varsayımından yola çıkarak, elektronların çekirdek üzerine düşmeyeceklerini söyledi. Elektronların ya daha üst bir yörüngeye ya da daha alt bir yörüngeye doğru, Planck kuantaları denilen hn miktardaki bir enerjiyle sıçrayabilirlerdi. Elektronlar, alt yörüngeye doğru sıçradıklarında bir enerji kuantumu yayınlar, üst yörüngeye doğru sıçradıklarındaysa bir enerji kuantasını soğurur. Atomda izin verilen enerji düzeyleri daha önce deneysel olarak incelenmiş ve ‘kuantum sayıları’ olarak sıralanmıştır.

Bohr’un kuantum fiziğine dayanan atom modeli, çok eskiden beri bilinen bir dizi fiziksel olguyu da açıklıyordu. Tayf analizi yıllardan beri biliminsanları tarafından kullanılan bir yöntemdi. Gazların soğurma ve yayınım çizgilerinin analizi, çeşitli maddelerin bileşimlerini ortaya çıkarmada çok yararlı bir teknikti. Örneğin 1895’te İngiliz astronom Joseph Lockyer (1836-1920) güneş tayfında bulduğu yeni bir çizgi serisinin “helyum” dediği yeni bir elemente ait olduğunu duyurmuştu. Bohr’un çözümü, bu tayf çizgilerinin gizemini de çözüyordu. Daha sonra Arthur Compton (1892-1962) saçılma deneyleriyle fotonların momentumunun elektronlara transferini ölçtü ve fotonların parçacık doğası kesinlik kazandı. 1927 yılında Nobel ödülü kazanan Compton’un çalışmaları atom altı fotonların gerçek ve kuantum fiziğinin doğru olduğunu kesin bir şekilde kanıtlamıştı. Sonunda artık kimsenin kuantum fiziğinin gerçekliğinden şüphesi kalmadı. Böylelikle birinci kuantum devrimi sonlanmıştı. Niels Bohr Nobel Ödülünü 1922’de aldı.

Ancak artık fizik bundan böyle eskisi gibi olmayacaktı: bütün kuram olasılıklara dayanıyordu. Einstein istemeden de olsa, kuantum fiziğine bir atomun daha sonra ne yapacağının asla hesaplanamayacağı fikrini sokmuştu.

Herhangi bir kuantum sayısına sahip herhangi bir atomun, önümüzdeki beş dakika içinde belirli bir frekansta bir foton yayınlama şansı hesaplanabilse de, bu olay milyonlarca yıl sonra bile meydana gelebilir. Kuantum fiziğinin hesapları deneylerle uyum içindedir çünkü deneylerde çok sayıda atom vardı. İstatistiksel olarak bir milyar atom içinden N adedinin t zamanı içinde bozunacağını hesaplarsınız ve bu deneylerle örtüşür. Ancak hangi atomun bozunup hangisinin bozunmayacağını söyleyemezsiniz. Bu fizik tarihinde ilk defa ortaya çıkan bir kavramdı. Klasik termodinamikte de olasılık hesapları yapılır. Ama kuramsal olarak tek bir molekülün hızını ve konumunu bilmek ve t zamanında nerede olacağını hesaplamak olanaklıdır. Bütün moleküllerin hızlarını ve konumlarını bilemeyeceğimiz için olasılık hesapları yaparız. Kuantum fiziğinde olasılık çok daha temeldir, doğaya içkindir. Zaten o nedenle Einstein ‘Tanrı zar atmaz’ diyerek bu yoruma karşı çıkmıştır. Şüphesiz Einstein’ın kastettiği tanrı burada doğanın kendisiydi. Einstein olasılıkçı bir doğaya inanmıyordu, ama tarih Einstein’ı haksız çıkardı.

İkinci kuantum devrimi: Schrödinger ve Heisenberg

Kuantum devriminin ikinci aşamasına giden yolda Fransız fizikçisi Louis de Broglie’nin (1892-1987) çalışmaları önemli rol oynar. Louis de Broglie 1924 yılında doktora tezinde parçacık olarak bilinen elektronların da bazı koşullar altında dalga gibi davrandıklarını öne sürer. Yine Einstein’ın çabalarıyla kabul gören bu görüş, Schrödinger’in dalga mekaniğini geliştirmesine yol açacaktır. De Broglie’nin tezini okuduktan sonra Schrödinder, dalgalara dayanan kuantum dünyasının tam, kendi içinde tutarlı bir kuramını geliştirir. O sıralarda Alman Werner Heisenberg de (1901-1976) kuantum dünyasının, parçacıklara dayalı, kendi içinde tutarlı tam bir kuramını geliştirmişti.

Schrödinger, en basit atom olan hidrojende elektronun davranışını açıklayacak bir dalga denklemi bulmak amacıyla, klasik mekaniğin standart dalga denklemiyle başlayarak, Broglie’nin bulduğu dalga boylarını momentumlara dönüştüren bağıntıları kullanarak, elektron için çok basit bir dalga denklemi elde etti. Schrödinger denklemi 19. yüzyılda, ışık ve diğer elektromanyetik dalgalar için Maxwell’in bulduğu denkleme benziyordu. Aslında ilk başta görelilik etkilerini de hesaba katmıştı ama göreli denklemin öngörüleri gerçek atomlarla yapılan gözlemlere uymuyordu çünkü elektronun kuantum spinini hesaba katmamıştı. Kuantum mekaniğine daha sonar giren spin fikrini de içeren göreli dalga denklemi yazma onuru Dirac’a kalacaktı.

Öte yandan 1925 yılında birçok fizikçi gibi Heisenberg de elektronların yörüngeler arasında sıçramalarıyla uğraşıyordu. Ölçülmediği zaman, bir atoma veya diğer herhangi bir kuantum birimine ne olduğunu bilme olanağının bulunmadığı anlaşılmıştı. Atomun belirli bir kuantum durumunda olduğunu gösteren bir ölçüm yapabilirsiniz, daha sonra bir başka ölçüm yaparak bir başka kuantum durumunda olduğunu gösterebilirsiniz. Ama bu ölçümler arasında atoma gerçekte ne olduğunu söyleyemezsiniz. Başlangıçta bu fikirden hoşlanmayan Heisenberg, böyle bir kuramın nasıl işleyeceğini görmeye karar verdi ve böylelikle matris mekaniğini geliştirdi. Kuantum sistemlerinde her gözlem aynı zamanda iki durumla uğraşır: bir atom tayfında belirli bir çizginin enerjisinin ölçülmesi; bir fotonun soğurulması ya da yayınlanması olaylarını içeren iki kuantum durumu arasındaki ilişkiyi gösterir.

Heisenberg’in matris mekaniği çok önemli bir sonuca yol açmıştı: matrisler yer değiştiremezler. Momentum ve konumun kuantum eşdeğerlerini karşılıklı olarak p ve q ile gösterirsek:

pq – qp = h/2πi

sonucu çıkar. Planck sabiti h’ın sıfır olduğu durumda, klasik fizikte beklenildiği gibi pq = qp sonucuna ulaşılır.

Heisenberg belirsizlik ilkesi adı verilen bu sonucun içeriğini şöyle tarif edebiliriz: Belli bir anda konum ne kadar kesin biçimde belirlenmişse, momentum o kadar az kesinlikte bilinebilir ve tersi de geçerlidir. Ayrıca belirsizlik ilkesi sadece konum ve momentuma değil, zaman ve enerji gibi başka nicelik çiftlerine de uygulanabilir. Diğer bir deyişle bir şeyi ne kadar kesin bilirseniz, bir başka şeyi o kadar az kesinlikte bilebileceğinizi söylemektedir. Hatta eğer bir niceliği tam olarak, eksiksiz tamlıkta biliyorsanız, hakkında hiçbir şey bilmeyeceğiniz başka bir nicelik vardır, anlamına gelmektedir.

Klasik fizikte bir karşılığı olmayan belirsizlik ilkesi kuantum fiziğinin temelinde yer alır. Klasik fizikte, bir parçacığın aynı anda hem konumunu hem de momentumunu bilememeniz için bir neden yoktur.

Belirsizlik ilkesi, matematiksel olarak şu şekilde yazılabilir:

DxDp ≥ h/4π veya DtDE ≥ h/4π.

Bu denklemlerde D’lar belirsizliği gösterir; değişkenler de konum x, momentum p, zaman t ve enerji E’dir. Belirsizlik ilkesinin zaman-enerji biçimi ontolojik açıdan çok önemli bir sonuçtur. Çok küçük bir zaman diliminde enerji korunum ilkesinin ihlal edilebileceğini söyler ve sanal parçacıkların yaratılmasına olanak sağlar.

Kuantum fiziğinin gizemleri

Schrödinger’in dalga denklemi sürekli bir olayı betimlerken, Heisenberg’in matrisleri kesikli bir işlemin açıklamasıdır. Bu iki kuramın da aynı sorunlara uygulandıklarında aynı yanıtı verdiği, dolayısıyla matematiksel olarak eşdeğer olduklarının anlaşılması bir sürpriz olarak ortaya çıktı. Matris mekaniğini dalga denkleminden çıkartmak için, Schrödinger’in dalga denkleminde konum ve momentumla ilgili değişkenler yerine, Heisenberg kuramındaki operatör olarak bilinen iki bağıntıyı koymak gerekir. Ama ortada açıklanamayan bir şey vardı: matris mekaniğiyle dalga mekaniği eşdeğerse, sürekli bir dalga fonksiyonuyla kesikli bir kuantum sıçraması nasıl açıklanabilirdi?

1926’da Max Born dalga fonksiyonunun yeni bir yorumunu ortaya atmıştı. Dalga fonksiyonuyla, elektronun uzayın herhangi bir noktasında bulunma olasılığının hesaplanabileceğini göstermişti (ki sonradan bu çalışmasıyla Nobel ödülü alacaktır). Born, elektronlar gibi parçacıkların gerçek varlıklar olduklarını, bunların bulundukları konumların bir dalganın genlik olasılığına bağlı olduğunu ileri sürüyordu. Ama Schrödinger (ve Einstein) gibi bazı fizikçiler bu fikirden pek hoşlanmadılar. Onlara göre buradaki sorun, elektron gibi bir parçacığın uzayda izleyeceği belirli bir yolun olmaması, sadece uzayın bazı bölgelerinde bulunma olasılığının hesaplanabilmesiydi. Schrödinger’e göre, kuantum sıçraması sırasında bir elektronun hareketini açıklayan bir yasa yoksa “kuantum sıçraması fikri tam bir fantezidir”. Bohr’a göreyse (Kopenhag görüşü) “bu kuantum sıçraması olmadığını kanıtlamaz, sadece onu hayal edemediğimizi kanıtlar”. Günümüzde bile çözümlenmemiş olan bu tartışma kuantum felsefesi alanında devam etmektedir. Ama günümüzde hemen bütün fizikçiler Kopenhag yorumunda birleşirler. Biz gözlemlemezken atomda neler olup bittiğini bilmiyoruz, ama gözlemlediğimiz zaman atomun ne durumda olacağını kuantum fiziği doğru bir şekilde betimliyor.

Kopenhag yorumunda bir kuantum biriminin, örneğin bir elektronun, gözlemlenmediği bir sırada, nerede olduğunu sormanın bir anlamı yoktur. Yorumun nasıl işlediğini anlamak için en iyi yol, kuantum dünyasının klasik gizemi olan çift yarık deneyine bakmaktır. Tıpkı Young’un çift yarık deneyinde olduğu gibi, bu sefer çift yarığa elektronlar gönderirsek, arkadaki ekranda girişim desenleri görürüz. Elektronlar iki yarıktan aynı anda geçiyorlarmış gibidir. Hangi yarıktan geçtiklerini ölçmeye kalktığımızdaysa bu sefer girişim deseni kaybolur, belli bir duruma ‘çökerler’. Elektron sadece biz onu gözlemlediğimizde varlığa kavuşur gibi görünür. Gerçek gözlemden bağımsız olarak, elektronun nesnel varlığına verilebilecek herhangi bir anlam yoktur.

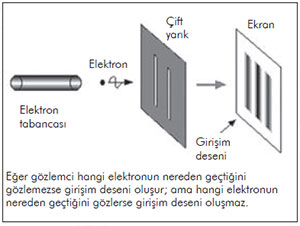Elektronlar gözlemlenmediğinde aynı anda iki farklı yerde birden olmaları diğer bir ifadeyle, üst üste binmiş durumları dolanıklık adı verilen bir olgudur. Klasik fizikte ya da içinde yaşadığımız makro-dünyada hiç karşılaşmadığımız dolanıklık, üst üste binmiş durumların kuantum etkilerinin normal mesafelerinin çok ötesindeki büyük uzaklıklara yayılabilmesini de içerir. Örneğin bir atomun taban durumundaki bir elektron aynı zamanda, her biri elektronu belli bir yerle sınırlı tutmuş sayısız durumun üst üste binmiş halidir. Sağduyumuza aykırı gelen bu fikre, Einstein bile hiçbir zaman sıcak bakmadı ve bunu çürütmek için birçok düşünce deneyi tasarladı. Ama sonunda haksız çıktı (Bkz: Bilim ve Gelecek, “Kuantum Dolanıklığı” Mart 2015). Artık biliyoruz ki mikro-dünyada kuantum birimleri dolanıktır.

Kuantumun tuhaf dünyası

Atom-altı ölçekteki mikro-dünyaya ilişkin fizik yasaları, günlük hayatta (makro-dünyada) aşina olduğumuz olgularla çelişir. Kuantum mekaniğinin ilk keşfedildiği yıllarda, bu olgular tam olarak anlaşılamamıştı ve kuantum mekaniğini geliştiren kimi ünlü fizikçiler (Niels Bohr ve Werner Heisenberg gibi) bile “nesnel gerçeklik savından”, yani gözlemlemediğimizde dünyanın var olduğu fikrinden vazgeçmemiz gerektiğinden söz ediyorlardı. Nesnel gerçeklik tartışması, bazı fizikçiler ve felsefeciler arasında hâlâ devam etmektedir; ama yapılan sayısız deneyler, kuramla gözlemler arasında çok büyük bir uyum göstermektedir. Kuantum mekaniği yasalarının geçerliliği sayısız deneylerle kanıtlanmıştır. Kullandığımız hemen her cihazda bunun kanıtlarını görürüz. Kuantum mekaniğini yanlışlamak için yapılan çok hassas deneyler ise henüz onun yanlış olduğunu ispatlamış değildir. Aksine çevremizde gördüğümüz hemen her şeyin açıklaması ancak ve ancak kuantum kuramı ile mümkün olmaktadır. Kuantum kuramı olmasa, Güneş’in neden parladığını, gökyüzünün neden mavi olduğunu, neden masanın üstünde duran kitapların yere düşmediğini, vb. gibi yüzlerce, binlerce olayı açıklayamayız. Ancak kuantum fiziğinin yasaları deneyleri doğru bir şekilde öngörse de, doğanın neden böyle davrandığını bilmiyoruz. Kuantum yasaları sağduyumuza çok aykırı gelmekte. Örneğin mikro-dünyada yerellik ilkesi ihlal edilmekte. Bir atom altı parçacık aynı anda faklı yerlerdeymiş gibi ele alınmakta. Kuantum fiziğinin doğayı ele alış biçimi, günlük hayatta alışık olduğumuz kavramlara çok aykırı. Oysa bizim yaşadığımız boyutlarda bir nesne aynı anda iki farklı yerde olamaz.

Çevremizde gördüğümüz her şey, hava, su, ateş ve toprak bir metrenin on milyarda biri büyüklüğündeki atomlardan; atomlar kendilerinden on bin kat küçük çekirdek ile bir milyar kat küçük elektronlardan; çekirdek ise kendinden on kat daha küçük nötron ve protonlardan oluşmaktadır. Atom çekirdeğindeki proton ve nötronlar ise temel parçacık olan kuarklardan meydana gelmektedir. Böylesi küçük varlıkların (mikro-dünya) davranışlarının günlük hayatta (makro-dünya) gözlemlediğimiz cisimlerden farklı olduğunu varsayıyoruz. Çok küçük boyutlarda geçerli olan kuantum mekaniği yasalarına göre, atom-altı parçacıkların konumları ne kadar yüksek hassasiyetle ölçülürse, hızları o kadar az hassasiyetle bilinebilir (Heisenberg belirsizlik ilkesi); hem dalga hem parçacık özellikleri gösterirler; devinim sırasında belli bir yörünge izlemezler; verilen bir durumdan diğerine geçerken gözlenemeyen ara durumlar geçirirler. Özetle, mikro-dünyaya uyguladığımız doğa yasalarıyla, makro-dünyayı değerlendirirken ortaya attığımız doğa yasaları arasında ontolojik bir kopuş söz konusu. Çünkü beynimiz makro-dünyada evrimleşti. Çevremizdeki olaylara tepki vermeye yönelik olarak evrimleşen zihnimiz, atom altı dünyasındaki günlük hayatta alışkın olmadığımız olguları yorumlamakta yetersiz kalıyor.

Örneğin yüksek enerjili çarpışmalarla parçacıklar yaratma olayına bakalım. Bu, büyük hızlandırıcılarda üretilen ve parçacıkların izlerini bıraktıkları kabarcık odaları ya da onların modern versiyonları olan elektronik dedektörler sayesinde gözlemlenen bir olaydır. İki protonu hızlandırırız. Her birinin belli bir hareketi, belli bir hızı, belli bir enerjisi vardır. Sonra protonları çarpıştırırız ve onlar birbirlerinden saçılırlar. Çarpışmadan sonra iki protonun yanında kütlesiyle, elektrik yüküyle, vs ile başlı başına farklı, başka parçacıklar olduğunu saptarız. Bunlar çarpışan protonların toplam enerjileri üzerinden, çarpışma esnasında yaratılmış parçacıklardır. Şüphesiz olay E = mc²denklemiyle gösterilen kütle-enerji eşitliği yasasına uygundur. Ama bunu alıştığımız kavramlar aracılığıyla tanımlamak isteseydik, çarpışan protonların hareketinin parçacıklara dönüştüğünü söylememiz gerekirdi. Oysa hareket nesnelerin bir özelliğidir ve sonuç olarak, bir nesnenin özelliğinin nesneye dönüştüğünü söylemiş oluyoruz. Bu bizim bildik kavramlarımızı tamamen aşan bir düşüncedir. Bizim bildik kavramlar çerçevesinde bir yanda nesneler, öte yanda konum, hareket, vs gibi bu nesnelerin özellikleri vardır ve bunlar birbirlerine asla dönüşmeyen iki kategoridir.

Bu olayı duyuların bize “gerçeği” göstermediği şeklinde de yorumlayabiliriz. Aslında nesnenin görüldüğü gibi olmadığını uzun zamandan beri biliyoruz. Klasik fizik bize maddenin bizzat “dolu”nun simgesi olduğunu öğretiyordu, oysa aslında başlı başına boşluktan (çekirdekler ve elektronlar arasındaki boşluk) oluşur. Ama bundan daha da öte bir olgu var kuantum fiziğinde. Nesnelerin birbirlerinden ayrılmazlığı var; diğer bir ifadeyle dolanıklılık, nesnenin farklı olma niteliğinin yokluğunun ifadesidir. Kuantum durumu evrenin geriye kalanıyla “dolanık” haldedir. Peki, nasıl oluyor da bize yerellik varmış gibi görünüyor? Daha çok yakın çok genel bir argüman -eşevresizlik kuramı, deniyor- bu olayı kısmen açıklıyor. Ama söz konusu açıklamanın çok şaşırtacak yanları var: Pratikte hiçbir büyüklüğü ölçemeyiz; ölçülmesi bize nesnesinin yerelliği olmadığını gösterirdi, çünkü bu ölçmeler çok karmaşıktır. (Belki evrendeki atom çekirdekleri kadar çok miktarda akıl almaz araçlar ve korkunç süreler gerektirirdi). Nesnelerin bizim onlarda gördüğümüz şekilleri ve konumları vardır ve bu kendiliğinden böyledir, bizim kendi kapasitemizin sınırlarından ya da evrenin boyutlarından, kısaca her şeyden tamamen bağımsızdır diyen klasik görüşten elbette çok uzağız, hatta tam karşısındayız. Bir benzetme gerekseydi, bu kuramın bize tanımladığı şekliyle nesneyi bir gökkuşağına benzetebilirdik. Arabada gidiyorsanız, gökkuşağı yer değiştirir. Siz durursanız, o da durur. Siz hareket ederseniz o da hareket eder. Öyleyse özellikleri kısmen size bağlıdır. Ve tabii, bütün bunlar gökkuşağının doğasına bağlı olduğundan, siz hareketsiz kalsanız da, özellikleri sanal olarak size bağlı olmaya devam eder. “Harfiyen” alınan ve evrensel olarak düşünülen kuantum fiziğinin gözünde, bütün nesnelerin bizim karşımızdaki statüsü aşağı yukarı budur. Bizim derken duyulara sahip varlıklar topluluğunu kastediyoruz. Elbette, fizikçiler klasik bakımdan daha nesnel bir görüşe dönmeye çalıştılar, ama dolayından geçmek zorunda kaldıkları o kadar ciddi engellerle karşılaştılar ki araştırmalarının sonuçları pek tatminkâr görünmüyor.

Son olarak şunu belirtelim ki, kuantum fiziği henüz tam olarak anlaşılmış değil. Evet, elimizde çok harika bir kuram var. Deney sonuçlarıyla bilim tarihinde hiç olmadığı kadar iyi uyum içinde (milyarda bir sapma gösteriyor). Ancak felsefi arka planı hâlâ eksik. Daha doğrusu kuantum fiziği bizim makro-dünyada şekillenmiş olan felsefemizi değiştirmemiz gerektiğini zorluyor.

Kaynaklar

1) Atomların Dansı, Marcus Chown, çev: İmge Tan, Alfa Bilim Dizisi, 2010.

2) Biraz Kuantumdan Zarar Gelmez, Marcus Chown, çev: Taylan Taftaf, Alfa Bilim Dizisi, 2010.

3) 101 Soruda Kuantum, Kenneth W. Ford, çev: Barış Gönülşen, Alfa Bilim Dizisi, 2013.

4) Çoklu Evrenler, John Gribbin, çev: Özge Kelekçi, Alfa Bilim Dizisi, 2013.

5) Erwin Schrödinger ve Kuantum Devrimi, John Gribbin, çev: Bahattin Mehmet Baysal, Alfa Bilim Dizisi, 2013.

6) Kuantum Mekaniğinin Felsefi Temelleri, Hans Reichenbach, çev: Deniz Ölçek, Alfa Bilim Dizisi, 2014.

7) Traité de physique et de philosophie, Bernard d’Espagnat, Fayard, 2002.