Dünyayı döndüren fizikçi: Galileo Galilei

Galileo Galilei (1564-1642) ile Roma Katolik Kilisesi’nin 17. yüzyılın ilk yıllarında karşı karşıya gelişi, Batı geleneğinde bilim ile din arasındaki çatışmanın klasik örneğidir. Bruno ve Kepler’le birlikte Copernicusçu bilimsel devrimi başlatan Galileo, modern bilim ve felsefeye çok yünlü katkıda bulunan tarihsel bir figürdür. Katkıda bulunduğu başlıca alanlar, matematiksel fizik, gözlemsel astronomi, bilim felsefesi ve doğa felsefesidir. Onun bilimsel çalışmaları Copernicus, Bruno ve Kepler’le başlayan çizgi üzerinde yer alır ve Newton’a kadar uzanır.

Galileo’nun matematiksel fiziği, akademik kariyerinin ilk yıllarından başlayarak kabul ettiği Copernicus’un güneş-merkezli astronomi sistemine bağlıdır. Diğer bir deyişle ancak güneş-merkezli bir evren modelinin kabul edilmesi halinde geçerli olabilecek bir fiziksel teori ileri sürmüştür:

“Peki, gezegenlerin görünür hareketlerine ne demeli? O kadar düzensiz ki hareketleri, yalnızca kâh hızlı kâh ağır gitme durumu sergilemekle kalmıyorlar bir de bazen durup bir miktar da geri gittikleri olmuyor mu? Bu görünümü kurtarmak için Batlamyus [Ptolemaios] büyük ilmekler (episikl) diye bir şey icat etmiştir ve her bir gezegene ilmek tanımıştır, birbiriyle ilişkisiz bazı hareketlere kurallar getirir, oysa tüm bunlara gerek kalmaz sadece Yerküre’nin döndüğü kabul edilirse.” (Galileo, 2008a: 472)

Galileo’nun matematiksel fiziği birdenbire ortaya çıkmış değildir. Tarihsel olarak birbirini takip eden Aristoteles fiziği, impetus fiziği ve matematiksel fizik evreleri Galileo’nun eserlerinde de bulunur. Onun ilk yapıtlarına Aristotelesçi yaklaşım egemendir; kozmoloji ya da fizik, 16. yüzyıl Avrupa üniversitelerinde öğretildiği biçimiyle yer almıştır. Aristoteles fiziğinin ilkelerini açıkça savunduğu bu yapıtlarını Arşimet fiziğinin belli bir yorumuna dayandırmıştır. Onun bu dönemde yazdığı La Bilancetta (Küçük Denge, 1586) adlı yapıtı Arşimet’in kavrayış biçim ve tekniklerinden esinlenir. Galileo’nun Pisa Üniversitesi matematik kürsüsüne profesör olarak kabul edilmesini sağlayan bu yapıtın ana konusu suya daldırılan katı cisimlerin ağırlık merkezleridir. Galileo’nun ilk İtalyanca çalışması olan bu eser günümüz fiziğinde hidrostatik (sıvıların dengesi) olarak bilinen alanla ilgilidir.

Galileo’nun Aristoteles fiziğine yönelik ilk eleştirileri Pisa Üniversitesi’nde profesör olarak bulunduğu dönemde, hareket üzerine yazdığı deneme ve incelemelerle başlamıştır. Benedetti’nin impetus teorisinden etkilenerek fiziği matematikselleştirme geleneğini devam ettirir. Ancak Benedetti’ye kıyasla impetus fiziğinin kavramlarını daha sistematik kullanır. Bu dönemde iki yönlü bir çalışma yürütür: Bir yandan tutarlı bir hareket analizi geliştirmeye çalışmış, diğer yandan fiziksel nesnelerin geometrik bir uzay içine nasıl yerleştirilebileceği konusunu ele almıştır.

Galileo serbest düşme sorununu De Motu Locali (Hareket Üzerine Notlar, 1589) adlı yapıtında ele alır. Bu Latince yapıtını Galileo 1589 yılında Pisa Üniversitesi’nde matematik profesörlüğü yaptığı sırada yazmıştır. 23 bölümden oluşan bu eser, kendisi gibi aynı üniversitede profesörlük yapan ve tipik Aristotelesçi düşünceleri temsil eden Francesco Buonamici’nin 1591 yılında yazdığı hareketle ilgili 1000 sayfalık kitabına karşılık kendi görüşlerini açıklama isteğinden doğmuştur. Büyük ölçüde Aristoteles fiziğinin etkisi altında yazdığı bu eserine göre hareket sürekli uygulanan bir kuvveti gerektirir (Akdoğan, 1996: 102). Galileo bu yapıtında “ağırlığın serbest düşme hareketi sırasında şu ya da bu yolla giderek artan bir impetus olarak kavranmasına” karşı çıkar. Ona göre ağırlık, cisimlerin temel özelliklerinden biridir ve sabittir. Galileo cisimleri ağırlıklarından bağımsız olarak ele almamış, yani ağırlığı cisme uygulanan bir kuvvetin sonucu olarak değil, cismin doğal bir özelliği olarak kavramaya devam etmiştir. Diğer yandan Galileo, ağırlıktan farklı bir olgu olduğunu düşündüğü impetusun daha doğru bir tanımını yapmaya yönelmiştir. Ancak cisimleri ağırlıklarından bağımsız olarak tanımlayamaması -aslında fiziğinde temel bir rol oynayan- eylemsizlik ilkesini formüle edememesine neden olmuştur.

Galileo, impetus kavramını açıklamak için “ateşte ısıtılan metal çubuk analojisi”ne başvurdu. Bu analojiye göre tıpkı ateşte ısıtılan bir demir çubuğun içindeki ısının, çubuk ateşten çekildikten sonra da bir süre çubukta kalması gibi, bir cisme aktarılan impetus da cismin içinde azalarak var olmaya devam ediyordu. Galileo serbest düşme hareketini impetus kavramıyla açıklamaya çalıştı. Bu açıklamaya göre yukarı doğru fırlatılmış bir cisme impetus kazandırılır ve impetus cismin hafiflemesini sağladığı için cisim yukarı doğru yükselir. Fakat impetus tıpkı ısı gibi azalarak tükendiği için bir süre sonra cismin ağırlığı ile denge durumu oluşur ve düşme hareketi başlar. Fakat impetus bütünüyle tükenmeyeceği için düşme hareketi esnasında, düşme hareketini -azalarak- engelleyen bir direnç fonksiyonu görür. Bu durumda, eğer cisim yeterli uzaklıktan düşerse impetusun tümü tükeneceğinden, cisim sonunda ivmeli olarak değil de, üniform, yani sabit bir hızla düşmeye başlayacaktır.

Ancak Galileo’nun impetus ve ağırlık kavramlarını bu şekilde kullanarak hareketi açıklama çabası, serbest düşme hareketi olgusuyla çelişen bir çıkarıma yol açtı: Düşme hareketi yapan bir cisim sabit bir kuvvet olarak kabul edilen ağırlığının etkisiyle hareket ettiğine göre bu cismin hızı da sabit olmalıdır. Çünkü sabit bir etki hiçbir zaman değişken bir sonuç doğurmaz (Koyré, 1990: 8). Ancak doğadaki cisimlerin artan bir hızla, yani hızlanarak düştükleri gözlenir. Galileo, teorisiyle olgular arasındaki uyuşmazlığı, bu kuralların yalnızca ağırlığın etkisiyle düşen cisimler için doğru olabileceğini söyleyerek aşmaya çalıştı: Fiziksel dünyada hiçbir cisim yalnızca ağırlığının etkisiyle düşmez. Ağırlık bir cisme hafiflikle birleşerek etkir. Bir cismin yükselmesi kendisine aktarılan “hafiflik”in cismin ağırlığından daha büyük olmasına bağlıdır. Galileo’ya göre, bu durumda cismin yukarı doğru yükselmesi, cismin ağırlığı ile cisme verilen hafiflik arasındaki farktan kaynaklanıyordu:

“Cisme aktarılan ‘hafiflik’ tırmanma hareketi boyunca sürekli azalacağına göre belli bir anda bu fark sıfıra eşit olacak ve cisim düşmeye başlayacaktır. Düşmenin başladığı an hafifliğin değil, hafiflikle ağırlık arasındaki farkın sıfıra eşit olduğu andır. Dolayısıyla, düşme süresince de cisimde azalmakta olan bir hafiflik vardır. Cisim ağırlık ve hafiflik arasındaki sürekli artan farkın etkisiyle düştüğü için de sürekli olarak hızlanmaktadır.” (Koyré, 1990: 8)

Aristoteles fiziğinde hafiflik cisimlerin yükselmesinin nedeni olarak ele alınmıştı. Galileo ise mutlak ve birbirinden farklı nedenler olduğu düşünülen “ağırlık” ve “hafiflik” kavramlarını eleştirdi ve etkilerinden yola çıkarak yeniden tanımladı. Galileo’ya göre, bir tahta parçasının havada yüksekten bırakıldığında düşmesi, suyun dibinde serbest bırakıldığında ise yükselmesi gibi gözlemler, Aristoteles’in söylediklerinin tersine, ağırlık ve hafifliğin mutlak değil göreli özellikler olduğunu gösterir. Bir cisim, içinde bulunduğu ortama bağlı olarak alçalır ya da yükselir. Cismi aşağı ya da yukarı doğru hareket ettiren kuvvet de, cismin ağırlığıyla cismin hacmine eşit hacimdeki ortamın ağırlığı arasındaki farkla ölçülür. Bunun sonucu olarak her cisim birim hacmindeki madde miktarıyla belirlenen bir ağırlığa sahiptir. Bu çıkarım, Aristoteles’in değil ama eski Yunanlıların “bütün cisimlerin yalnızca ağırlığı vardır, hafif cisim yoktur” biçimindeki görüşlerine uygundu. Bu tanıma göre yukarı doğru doğal hareket söz konusu değildir. Hiçbir ağır cisim kendiliğinden yükselmeyeceği için Galileo’nun varlığını kabul ettiği tek doğal hareket cisimlerin ağırlıklarının etkisi altında dünyanın merkezine doğru yaptıkları harekettir. Bu hareket aynı zamanda doğal ereğe sahip tek harekettir.

Galileo’nun mutlak ve göreli ağırlık ayrımı ve düşme hızını cismin içinde hareket ettiği ortamın içindeki göreli ağırlığının bir fonksiyonu olarak tanımlanması, cisimlerin yalnızca boşlukta mutlak ağırlıklarıyla hareket edebilecekleri anlamına geliyordu. Bu çıkarım Aristoteles fiziğinin en temel ilkeleriyle çelişiyordu. Çünkü Aristoteles fiziğinde boşluk yoktu. Bu çıkarımın Aristoteles fiziği ile çelişen bir yönü de, hareketin, cismin içinde taşınan bir kuvvetin etkisiyle oluştuğu görüşüdür (Koyré, 1990: 9).

Pisa’da ilk çalışmalarından beri Galileo’nun amacı matematiksel bir fizik kurmaktı. Bu amaçla önce impetus kavramına dayalı matematiksel bir fizik kurmayı denedi. Öncelikli sorunu maddenin ölçülemeyen bir özelliğini tanımlayan karmaşık ve belirsiz impetus kavramının nasıl matematiksel hale getirilebileceğiydi. Örneğin, impetusun sürekli azalışı nasıl hesaplanacaktı? Ancak bu çözümü olanaksız bir soruydu. Çünkü söz konusu sorunun nihai çözümü için impetus kavramının hareket ve momentum kavramlarıyla yer değiştirmesini, yani Newton’u beklemek gerekmiştir. Galileo’nun çözmeye çalıştığı diğer bir soru şuydu: İmpetusun cismin içinde birikmesi nasıl açıklanabilir? Bu sorunun çözümü ise impetus kavramının radikal bir dönüşümünü, yani yeniden tanımlanmasını gerekli kılıyordu. Bu nedenle Galileo impetusu, cisme içsel nedenlerin ürettiği bir nitelik olarak değil, dışsal bir hareket ettiricinin hareketin sürmesini sağlayacak sürekli etkileri sonucu oluşan bir nicelik olarak yeniden tanımladı.

İmpetus fiziği bir yönüyle Aristotelesçi bir özellik taşıyordu. Gerçekte impetus, Aristoteles’in dışsallaştırmış olduğu hareket ettirici kuvvetin, içselleştirilerek hayal gücünde canlandırılmasıydı (Grant, 1986: 58). Bu kavram, Aristoteles’in “hareket eden her şey bir diğeri tarafından hareket ettirilir” görüşüne bağlanmanın başka bir yoluydu. Matematiksel fizikle karşılaştırıldığında impetus fiziğinin, Aristoteles fiziğinin sağduyu ve günlük deneyimler temelinde eleştirilmesine dayanan tepkisel bir yaklaşımı temsil ettiği görülür. Ayrıca impetus kavramı, tüm inceliklerine karşın geometrik bir evren tasarımıyla bir türlü uyum içinde değildi. Dolayısıyla Aristoteles fiziğini reddettiği Pisa döneminde Galileo’nun sağduyu üzerine kurulu bir fizik geliştirme çabası başarısız oldu. Daha sonra çalışmalarını matematiksel bir fizik teorisi geliştirmek üzerinde yoğunlaştıran Galileo, önceki teorinin çelişkilerini tutarlı bir bütün içinde yeniden ele aldı ve fiziksel nesneler konusunda yeni bir kavrayış biçimi geliştirmeye çalıştı.

Serbest düşme sorunu
Pisa’dan Padova’ya geçen Galileo bu döneminde serbest düşme sorununa odaklandı. Ayrıca yeni fiziğin temel yasası üzerinde çalıştığının farkındaydı. Daha önce Arşimet’in uygulamış olduğu metodolojik bir kuralı, “bir sorun hakkında aynı anda birçok soru sorulmamalıdır” ilkesini serbest düşme sorununa uyguladı. Daha önce cisimlerin hem nasıl hem de neden hareket ettiklerini aynı anda açıklanmaya çalışan Galileo artık neden’i bir yana bırakıp nasıl’ı açıklama yoluna gitti (Bixby, 1997: 19). Serbest düşme hareketinin doğru bir şekilde açıklanması matematiksel fiziğin temelini oluşturacak kadar önemliydi.(1) Galileo, serbest düşme hareketiyle ilgili görüşlerini 16 Ekim 1604’te bilimsel konularda da yazmış olan Venedikli hukukçu, teolog ve tarihçi Paolo Sarpi’ye (1552-1623) yazdığı bir mektupta ifade etti:

“Bugüne dek, hareket problemleriyle ilgili gözlemlediğim özellikleri kanıtlamak için aksiyom olarak kabul edebileceğim kesin bir ilkeden yoksundum; fakat bu problemler üzerinde düşünürken, sonunda yeterince doğal ve açık gibi görünen bir önerme elde ettim; bu önerme doğru olarak kabul edildiğinde geriye kalan her şeyi, özellikle de doğal hareket (serbest düşme hareketi) sırasında kat edilen yolların birbirine oranının zamanların karelerinin oranına eşit olduğunu, ayrıca bunun sonucu olarak, eşit zaman aralıklarında katedilen yolların birden başlayan ardışık tek sayılarla orantılı olarak arttığını ve daha başka birçok şeyi gösterebiliyorum. Bu ilke de şu: doğal hareket (serbest düşme hareketi) yapan bir cisim, hızını, başlangıç noktasından itibaren kat ettiği yolla orantılı olarak arttırır.” (Koyré, 1990: 10)

İlk anda kendisinin de farkına varamadığı bir hatasından dolayı, bu mektupta dile getirdiği görüşleri Galileo’yu fiziği için aradığı temel ilkeye ya da teorisini üzerine inşa edebileceği aksiyoma ulaştıramamıştır. Bulduğunu sandığı “aksiyomatik ilke”nin, ona yüklediği rolü yerine getiremediğini fark ettiğinde Galileo hatasını anladı. Çünkü söz konusu ilkeden elindeki betimleyici bir formül olan “serbest düşme hareketi sırasında kat edilen yolların birbirine oranının zamanların karelerinin oranına eşit olduğu” gibi bir tanımı elde etmesi olanaksızdı. Galileo, serbest düşme sorununu tekrar tekrar kontrol ederek hatasının nerede olduğunu araştırdı ve buldu: Hareket ve zaman arasındaki sıkı ilişkiyi dikkate almamak (Koyré, 1990: 11).

Galileo’nun sabit ivmeli hareket tanımına göre bir cismin hızı harekete başladığı noktadan itibaren sürekli artar. Yani cisimler harekete başladıklarında çok küçük (sonsuz) bir yavaşlıkla hareket eder. İlk kez 1632 yılında İtalyanca yayınlanan Dialogo sopra i due massimi sistemi del mondo, tolemaico e copernicano (Galileo’nun ‘İki Büyük Dünya Sistemi Hakkında Diyalog’ adıyla 375 yıl sonra Türkçeye çevrilen bu ünlü yapıtı bu metinde kısaca ‘Dialogo’ olarak anılacaktır.) adlı yapıtında Galileo, -cisimlerin durgunluk halinden harekete nasıl geçebileceği, minimum ya da çok yavaş hareketin nasıl mümkün olabileceği gibi konulara da girerek- bu sorunu tartışmaya devam etti.

Dialogo’da Sagredo, “Galileo’nun ivmeli hareket açıklamaları konusunda matematiksel olarak yapılanların doğruluğunu kabul ettiğini ancak tanım ve önermelerin doğadaki serbest düşme hareketiyle uyuşup uyuşmadığı” noktasında şüpheleri olduğunu söyler. Sagredo’ya göre, “zaman sınırsız bir şekilde bölünebiliyorsa, cismin bir önceki anda sahip olduğu hız, var olan hızından sabit bir oranla daha az olacaktır. Bu şekilde durgun bir konumdan harekete geçen bir cismin belirli bir anda çok küçük bir hıza sahip olduğu söylenebilir.” (Koyré, 1990: 14) Ancak Sagredo, gözlemlenen cismin ilk anda büyük bir hıza sahip olduğunu belirterek bu iddiayı kabul etmez. Aslında Sagredo kinematiğin soyut akıl yürütmelerine kendi gözlemleriyle karşı çıkar. Bu gözlemler sağduyuya dayalı gözlemler, yani Aristotelesçi anlayışla yapılmış gözlemlerdir. Aslında Galileo serbest düşme hareketini açıklarken bu gözlem ve deney türünü de eleştirmek zorunda kalmıştır.

Galileo Dialogo’da ivmeli hareketi “sabit ivmeli hareket, hız derecelerinin, durgunluk halinden başlayarak, hareketin ilk anından itibaren ilerleyen zamanla birlikte arttığı hareket” olarak tanımladı ve düşme hareketiyle ilgili şu sonuca ulaştı:

“Durgunluk halinden başlayarak ivmeli hareketle düşen bir cismin belirli bir süre içerisinde belirli bir yol kat ettiğini ve belirli bir hıza kavuştuğunu varsayalım, cisim bu hızla ivmesiz bir hareket yapmış olsaydı, aynı süre içinde, ivmeli hareketle kat ettiği yolun iki katını kat etmiş olurdu.” (Koyré, 1990: 16)

Galileo’nun eserlerinde hem fizik hem de metafizikle ilgili sorunlar birlikte ele alınır. Fiziksel bir sorunu matematiksel bir yöntemle ele almanın yol açacağı metafizik sorunların da farkında olan Galileo, düşme hareketi ile ilgili yukarıdaki sonucun kesin doğru olduğunu savunmamış, yalnızca “mümkün” olduğunu söylemekle yetinmiştir. Bunun nedeni “matematiksel düşüncenin doğa bilimlerinde yeri” olarak tanımlanabilecek metafiziksel sorunun o dönemde henüz bir çözüme kavuşmamış olmasıydı. Galileo’nun matematiksel kanıtlamaya dayalı bilimsel önermeleri, Aristoteles fiziğinin “fiziksel bir uzayda düşen gerçek cisimler geometrik bir uzayda düşen soyut cisimlere benzemezler” (Koyré, 1990: 16) kabulü ile uyum içinde değildi. Matematiksel önermelerin fiziksel nesneler için de geçerli kabul edilebilmeleri, her şeyden önce Galileo fiziğinin temel dayanağını oluşturan doğayı matematikselleştirmenin meşru kabul edilmesine bağlıydı.

Galileo Dialogo’dan altı yıl sonra, 1638 yılında, Engizisyon yasağı yüzünden İtalya’da değil Hollanda’da yayınlanan Discorsi e dimostrazioni matematiche, intorno a due nuove scienze (İki Yeni Bilim Üzerine Konuşmalar) adlı yapıtında, farklı bir tutum izleyerek fiziksel dünyanın gerçek yasalarını keşfetmeyi amaçladı. Bu nedenle ele aldığı sabit ivmeli hareket çalışmalarını iki farklı düzeyi kapsayacak şekilde tasarladı. İlk düzeyde sabit ivmeli hareket yapan cismi soyut bir şekilde ele aldı ve olayın tamamen geometrik bir analizini yaptı. Galileo’nun bu düzeyde ele aldığı hareket duyulur bir cismin duyulur bir hareketi değil, ancak zihinde tasarlanabilir “soyut” bir cismin geometrik bir uzaydaki hareketiydi. İkinci düzeyde Galileo, bu analizini “gerçek” olay ile karşılaştırdı. Bu nedenle açıklamalarını, bu kez, mümkün olarak nitelemedi ve sonucu kanıtlanmış gibi önceden söyledi:

“Durgunluk halinden başlayarak ivmeli hareket yapan bir cismin belirli bir uzaklığı kat etmesi için gereken süre, aynı cismin bu uzaklığı ivmeli hareketinin maksimum ve minimum hız derecelerinin ortalamasına eşit sabit bir hızla yapacağı hareketle kat etmesi için gereken süreye eşittir.” (Koyré, 1990: 17)

Galileo’nun bu görüşü Dialogo’daki görüşünden daha kapsamlıydı. Yani bu görüş yalnızca serbest düşme hareketi için değil, tüm sabit ivmeli hareketler için ve herhangi bir zaman aralığı için geçerliydi. Ancak bu görüşe göre hareketin ele alındığı zaman aralığı sonlu olmak zorundaydı. Zaman ile hareket arasındaki sıkı ilişkiyi göstermek ve zamanın öncelikli rolünü tanımlamak isteyen Galileo Discorsi’de ikinci bir teorem ortaya koydu:

“Düzgün ivmelenen bir hareketle düşen bir cismin herhangi iki farklı zaman aralığı boyunca kat ettiği yolların birbirine oranı zamanların çift oranına, yani zamanların karelerinin oranına eşittir.” (Koyré, 1990: 17)

Bu teorem serbest düşme yasasının doğru tanımını ifade eder. Alınan yolu geçen zamanın fonksiyonu olarak doğrudan doğruya veren bu formül, bu başarısının yanı sıra ardışık tek sayılar yasasını da kolayca açıklayabilmektedir. Kısaca, doğadaki ivmeli hareket, zaman kavramı olmadan açıklanamaz. Galileo’nun daha önceki açıklamalarında başarısız olmasının nedeni, hareketi bir bütünlük içinde ele almaması olmuştur. Zamanın hareketle olan sıkı ilişkisini göz ardı etmiş olan Galileo bu hatasını düzelterek yeni bir teoreme ulaşmıştır. Galileo’nun zamanın öncelikli rolüne ilişkin sonraki görüşü teoremde ifade edilmekle kalmaz; bu teoremi kanıtlarken kullandığı geometrik şekillere de yansır. Galileo serbest düşme teoremini kanıtlarken bir değil iki geometrik doğru kullanır; doğrulardan biri alınan yolu ifade ederken ikinci doğru bağımsız bir biçimde akıp giden zamanı ifade eder. Bu yaklaşımı sayesinde Galileo serbest düşme hareketi sorununu kesin olarak çözmeyi başardı. Hareketsiz bir cismin düşerken kat ettiği mesafenin, geçen sürenin karesi kadar arttığını bulmuştu.

Aristoteles fiziğine karşı kendi hareket teorisini Dialogo’da temellendiren Galileo, dinamik ile kinematiği birbirinden ayırmış ve 14. yüzyıl kinematiğini sistemleştirerek hareketi kinematik bir çerçevede ele almıştır. Hareketin nedeni olan dinamikten farklı olarak kinematik hareketin nasıl meydana geldiğiyle ilgilidir. Dinamik ve kinematiğin uzun bir tarihi vardır. Aristoteles dinamik alanında önemli gelişmeler sağladığı halde -yol ve zaman kavramlarını kullanma dışında- kinematik alanına katkı sağlamamıştı (Akdoğan, 1996: 78). 14. yüzyıl kinematikçileri hareketi niteliklerle açıklamaya çalışırlarken hız, anlık hız ve ivme gibi yeni kavramlara ulaşmışlardı. Anlık hız hareketin bir andaki hızını, ivme hareketin hızında oluşan değişme oranını bize verir. Düzgün ivmeli harekette bir cismin hızı eşit zaman aralıklarında eşit miktarda artar. Ancak 14. yüzyıl kinematikçileri düzgün ivmeli hareket için bir örnek vermemişlerdi. Bu nedenle kinematik, İspanyol asıllı Dominiken bir papaz ve teolog olan Domingo de Soto’nun (1494-1560) 1545 yılında yazdığı bir kitapta düzgün ivmeli harekete örnek olarak düşen cisimlerin hareketini vermesine kadar soyut bir özellik taşıdı. Domingo de Soto’nun görüşünü kabul eden Galileo, daha çok başkalarını ikna etmek amacıyla eğik düzlem üzerinde düşme deneyleri yaptı (Akdoğan, 1996: 103). Galileo bu ölçümler ışığında hazırladığı cetvele dayanarak, toplam uzaklığın zamanın karesine eşit olduğunu gösterdi. Galileo serbest düşmede geçerli olan ivmeli hareket ilkesini deneyden çıkarmadı ama yalnızca deneylerle doğruladı (Akdoğan, 1996: 104). Bir bakıma 14. yüzyıl kinematiğini sistemleştirerek serbest düşen cisimlerin bilimine dönüştürdü. Bu dönemde yaptığı hareket üzerine çalışmaları üç temel ilke üzerine kuruludur: Hareketin göreliliği, hareketin bağımsızlığı ve hareketin korunumu.

Hareketin göreliliği
Galileo’nun hareketin göreliliği ilkesi hareketin optik göreliliği ilkesi ile karıştırılmamalıdır. Hareketin optik göreliliği, konumları ve hızları farklı olan gözlemcilerin bir cismin hareketini farklı biçimlerde görmeleri demektir ve bu çok eski zamanlardan beri bilinen bir ilkedir. Ayrıca hareketin optik göreliliği ilkesi, Aristoteles’in hareketin mutlaklığı ilkesiyle çelişmez. Aristoteles fiziği açısından optik görelilik, evrenin hareketsiz merkezine göre tanımlanan mutlak bir hareketin, farklı gözlemciler tarafından farklı hareketlermiş gibi görüleceğini ifade eder. Bu durumda yalnızca görünüşle ilgili bir görelilik söz konusudur (Koyré, 1990: 18). Galileo ise Dialogo’da hareketin gözlemci açısından göreliliğinden söz etti ve bu göreliliği “kendimizin de katıldığı hareketleri algılamamızın olanaksızlığı” olarak tanımladı. Örneğin Yer’in kendi etrafındaki günlük dönme hareketini hem Yer’e hem de gök cisimlerine atfedebiliriz. Bir gözlemci olarak bizim de katıldığımız hareketleri algılamamızın olanaksızlığını ileri sürerken, gözlemci açısına bağlı görelilikten daha geniş bir anlam taşıyan hareketin fiziksel ya da mekanik göreliliği fikrini ortaya atıyordu. Hareketin fiziksel göreliliği, hareketin yalnızca başka bir cisme göre tanımlanan bir hâl olarak ele alınması durumudur. Ayrıca, hareketin fiziksel göreliliği, hareketin görsel göreliliğinin eşdeğeridir. Hareket, harekete katılan biri tarafından algılanamıyorsa hareket onun için sanki yok gibidir. Tıpkı bunun gibi Yer’in hareketinin de Yer’in üzerinde meydana gelen olaylar üzerinde hiçbir etkisi olmaz. Galileo hareketin göreliliğini Salviati’nin ağzından -20. yüzyıl başlarında Einstein’ın rölativite/görelilik teorisini ortaya atmasından sonra oldukça popüler olmuş ve bilim basınında sıkça alıntılanmış- şu satırlarla ifade eder:

“Büyük bir geminin güvertesi altında olan bir kamaraya çekiliniz bir arkadaşınızla beraber ve bu kamarada sinek, kelebek ve benzeri uçan hayvancıklar bulunsun; burada bir de akvaryum olsun, içinde birkaç küçük balık dolaşan; yüksek bir yere bir küçük kova asın ve bu kovadan onun altındaki dar ağızlı bir kaba damlaya damlaya su aksın. Gemi duruyor vaziyetteyken uçan hayvancıkların eşit hızla kamaranın her yanına doğru uçtuklarını dikkatle izleyin; balıkların hiç kimseye aldırmadan her yöne doğru koşuştuklarını göreceksiniz. Su damlalarının hepsinin alttaki kabın ağzından girdiklerini göreceksiniz ve siz arkadaşınıza bir eşya atmayı denediğinizde, uzaklıklar eşit olmak şartıyla, daha büyük bir zahmet harcamadan bir yöne ya da öbür yöne atmak arasında fark olmadığını da göreceksiniz ve alışılmış deyimle, bacaklarınızı birleştirerek atlarsanız, her yöne doğru eşit mesafe aldığınızı göreceksiniz. Sıraladığım tüm bu olguların aynen gerçekleştiğini titizlikle gözledikten ve gemi duruyor olduğunda da bu olguların aynen gerçekleştiğinden emin olduktan sonra, gemiyi istediğiniz hıza ulaştırın (yeter ki geminin hızı hep aynı, tekdüze olsun ve tekneyi sağa sola iten dalga da olmasın) belirttiğim etkilerle aynen karşılaşacaksınız ve hiç fark olmayacak, gemi duruyor mu hareket halinde mi hiç fark etmeyeceksiniz.” (Galileo, 2008a: 258-259)

Hem Galileo’ya hem de Aristoteles’e göre, yer değiştirme hareketinin tanımlanabilmesi için bir referans (karşılaştırma) noktasının varlığı zorunludur. Aristoteles için, söz konusu referans noktası, hareketsiz kabul ettiği evrenin (aynı zamanda Yer’in) merkeziydi. Galileo için ise herhangi bir ikinci cismin varlığı yeterliydi. Yani ona göre hareketi tanımlayabilmek için hareketten mutlak bağımsız bir noktanın ya da cismin varlığı zorunlu değildi.

 Hareketin bağımsızlığı ve korunumu
Hareketin göreliliği ilkesinden çıkan bir sonuç da şudur: Bir cisim üzerinde aynı anda birden fazla hareket birlikte var olabilir (uyuşabilir) ve bir hareket başka bir hareketi engellemez. Bunun nedeni yukarıda ifade edildiği gibi aynı cismi hareket ettiren hareketlerin, birbirlerine göre sanki yok gibi olmalarıdır. Galileo’ya göre hareket, hareket eden cisimde bir değişiklik meydana getirmediği için cisim aynı anda birden fazla harekete sahip olabilir. Yani bu hareketler birbirini engellemezler ve birleşerek tek bir yörünge izlerler. Bir cisim üzerinde birden fazla hareketin aynı anda ve uyum içinde mevcut olması anlamına gelen hareketin bağımsızlığı ilkesi de Aristoteles fiziği açısından kabul edilemez bir görüştü.

Galileo’nun hareket açıklamaları, hareketin uzaydaki ayrıcalıklı noktalara ve ayrıcalıklı yönlere gerek olmadan tanımlanabilmesini sağladı. Bu önemli adım sayesinde fiziksel uzayın geometrik bir uzay olarak ele alınmasının önü açıldı. Ne var ki Galileo, bu noktada bir adım daha atıp eylemsizlik (inertia) ilkesini formüle etmeyi başaramadı. Yani hiçbir dış etki olmaması durumunda doğrusal hareketin sonsuza dek süreceğini açıkça söyleyemedi. Peki, Galileo bu ilkeyi neden tanımlayamadı? Çünkü eylemsizlik ilkesi Galileo’nun fizik teorisinin bütünlüğü içinde tam olarak tanımlanamazdı. Bununla birlikte eylemsizlik ilkesini tanımlama çabasını bırakmamıştır.

Ona göre, hareketi doğal hareket ve zorlama hareket olarak ikiye ayırmak ve uyuşmaz kabul etmek doğru değildi. Aynı zamanda hem doğal hareket, hem de zorlama hareket olarak kavranabilecek hareketler mevcuttur. Örneğin göksel kürelerin dairesel hareketleri ne yalnızca doğal, ne de yalnızca zorlama hareket olarak ele alınabilir. Çünkü bu kürelerin evrenin merkezine uzaklıkları hep aynı kalır; alçalma ya da yükselme hareketi yapmazlar.

Bu örnekten hareket eden Galileo yatay bir düzlem üzerinde yuvarlanan ağır bir kürenin hareketinin sonsuza dek sürebileceğini savunmuştu. Ancak bu kürenin üzerinde hareket edeceği yatay düzlemi de düz bir çizgi olarak değil “bütün noktaları evrenin merkezine aynı uzaklıkta olan, yani küresel bir yüzey” olarak ele aldı. Ona göre küresel bir cisim, ancak küresel bir yüzey üzerinde alçalıp yükselmeden, dolayısıyla da hızlanıp yavaşlamadan sonsuza dek hareket edebilir (Koyré, 1990: 20). Yani kürenin üzerinde hareket ettiği düzlem düz bir çizgi biçiminde olsaydı küre hareketini sonsuza kadar sürdüremezdi.

Galileo’nun bu görüşünü bir bakıma “dairesel eylemsizlik ilkesi” (Trusted, 1994: 50) olarak adlandırmak mümkündür. Çünkü Galileo, bu tanımında hareketi, ağır cisimlerin doğal özelliklerinden bağımsız olarak ele alamadığı gibi hareketin üzerinde gerçekleştiği yatay düzlemi küresel bir düzlem olarak ele alır. Nitekim Galileo şöyle der:

“Üzerine herhangi bir etki yapılmayan hareket halindeki bir cisim, dairesel bir yörünge üzerinde hızını sonsuza kadar korur.” (Vigoureux, 2008: 232)

Hareketin korunumu sorunu impetus kavramı ile yakından ilgiliydi. Fiziğinde bu kavramını yeniden tanımlayan Galileo impetusu hareketin nedeni olarak değil bizzat hareketin kendisiyle özdeş olarak ele aldı. Hareket ise, hareket eden cismin kendisine aitti. Galileo’nun Dialogo’daki deyişiyle:

“Bir yüzeyin ne alçalması, ne de yükselmesi için bütün parçalarının merkezden aynı uzaklıkta olması gereklidir. (…) Durgun bir suyun yüzeyi böyle bir yüzeydir. (…) Durgun bir su üzerinde yüzen bir gemiye bir kez belli bir itme verildiğinde, gemi düzgün bir biçimde sonsuza dek hareket edecektir. Geminin direğinin tepesine yerleştirilmiş bir taş da aynı şekilde bir daire üzerinde hareket edecek ve bu hareket dış bir engel söz konusu olmadığı sürece taştan silinmeyecek bir hareket olacaktır. Taşın hızının da geminin hızıyla aynı olacağı açık değil midir?” (Koyré, 1990: 21)

Hareket halindeki geminin direğine yerleştirilmiş olan taş, geminin impetusunu direkten ayrıldıktan sonra da barındırmaya devam eder. Taşın bu yatay ya da dairesel hareketi, taşın aşağı doğru hareketini etkilemez. Yani taşın aşağı düşmesi ne engellenir ne de gecikir. Bundan çıkan sonuç şudur: Geminin hızı ne olursa olsun taşın direğin tepesinden dibine düşerken geçen süre aynı taşın gemi hareketsizken yaptığı düşüş için geçen süreye eşittir. Ancak Galileo böyle bir deneyi asla gerçekleştiremedi. Buna benzer bir deney 1642 yılında Marsilya’da Pierre Gassendi tarafından yapılmıştır (Vigoureux, 2008: 236). Benzer bir şekilde, bir kulenin tepesinden yatay bir doğrultuda ateşlenen bir top mermisi, hiçbir itme uygulanmadan kulenin tepesinden bırakılan bir top mermisi ile aynı anda yere düşer. Gerçi ateşlenen mermi yere düşerken geçen sürede kilometrelerce yol kat eder ama bu durum düşme hızını etkilemez. Galileo’nun yeni fiziğinde hareketin korunumu “artık yalnızca dönme hareketi ya da evrenin merkezi etrafındaki dairesel hareket için geçerli bir ilke olmaktan” çıkar ve dairesel hareket dâhil her tür hareketi kapsayacak bir biçimde ele alınır.

Hareketin bu şekilde ele alınması dairesel hareketin ayrıcalıklı konumu ile çelişse de bu çelişki Dialogo’da açıkça dile getirilmemiştir. Ancak Discorsi adlı yapıtında bir adım daha atan Galileo küresel yüzey görüşünden kurtulmayı başarmıştır. Bu yapıtında bir cismin “ağırlık çizgileri”ni küresel bir yüzeyin merkezine yönelik olarak değil birbirine paralel olarak ele aldı: “Yatay bir düzlemin üzerinde duran bir cismin ağırlığı, düzlemin her noktasında düzleme dik olacaktır. Böylece, yatay bir düzlemin üzerinde hareket eden bir küre, doğrusal hareketini sonsuza dek sürdürecektir.” (Koyré, 1990: 21) Galileo, küresel yüzey görüşünü terk etmiş olsa da, ağırlığın, cisimlerin doğal bir özelliği olduğu görüşünü muhafaza etmiştir. Ona göre cisimler, evrende tek başlarına da kalsalar, doğal bir özellik olarak ağırlığa sahip olacaktı. Bir kürenin doğrusal hareket yapabilmesi, ancak altına ağırlığının etkisini yok edecek yatay bir düzlem konulmasıyla mümkündü. Yani yatay bir düzlem üzerinde sürekli doğrusal hareket yapmakta olan bir küre, altından bu düzlem çekildiğinde doğrusal hareketine son verir ve ağırlığının etkisiyle “aşağı” düşmeye başlardı.

Tıpkı Aristoteles gibi Galileo da ağırlığı cisimlerin doğal bir özelliği olarak kavradı. Ağırlık kavramından kopamaması onun önündeki en büyük epistemolojik engellerden biriydi ve bir bakıma eylemsizlik ilkesini tanımlamasını engelliyordu. Galileo’nun hareketle ilgili görüşleri, bu biçimiyle, eylemsizlik ilkesinin tam bir tanımı olarak kabul edilemez. Eylemsizlik ilkesinin içeriğini ve anlamını tam olarak kavrayan Galileo değil Descartes olmuştur.

Galileo doğrusal hareketin sonsuza kadar korunumu anlamında eylemsizlik ilkesini hiçbir yapıtında açıkça ifade etmemiş olsa da, şüphesiz, bu ilkeyi gündeme getiren ilk fizikçiydi. Hatta Galileo’nun eylemsizlik ilkesini tanımlamaya oldukça yaklaştığı anlar olmuştu:

“Sakin bir denizde yolculuk eden bir gemi, ne aşağı ne de yukarı doğru eğimi olmayan yüzeylerden birinde giden bir cisim olması itibariyle, kendisi bir defacık bir hareket gücüne sahip kılındı mıydı kesintisiz ve hep aynı hızla hareket etmeye müsaittir, elbet rastlantısal ve dış kaynaklı tüm engellerin giderilmiş olması şartıyla.” (Galileo, 2008a: 204)

Newton’un eylemsizlik ilkesini keşfeden kişi olarak Galileo’yu işaret etmesi yerindedir. Çünkü Galileo’nun mekaniği örtük bir biçimde de olsa eylemsizlik ilkesi üzerine kurulmuştu. Sonuç olarak, Newton fiziğinde temel ilke durumunda olan eylemsizlik ilkesi (yani bir cisme dışarıdan bir kuvvet etki yapmadıkça mevcut durumunu koruması) Galileo’nun buluşu olarak kabul edilmelidir. Tam bir tanımını verememiş olsa da eylemsizlik ilkesini keşfetmesi Galileo’nun bilime yaptığı katkıların başında yer alır.

Fırlatılan cisimlerin hareketi
Aristoteles’e göre hareketli bir cisme hareket ettiği sürece bir dış kuvvet etki eder. O dış kuvvet ortadan kalktığında hareket sona erer. Aristoteles fiziğinin Ortaçağ yorumunda, fırlatılan bir cismin düz bir hat boyunca bir noktaya kadar ilerledikten sonra yine düz bir hat boyunca aşağı doğru düştüğü varsayılıyordu (Tez, 1995: 15). Örneğin bir savaş sırasında fırlatılan bir top güllesinin düz bir hat boyunca uçtuktan sonra hedefin üstüne dik bir açıyla düştüğü sanılmaktaydı. Temeldeki varsayım şuydu: Bir cismin fırlatıldığında önce düz bir çizgi boyunca zorlama hareket yapar, sonra cismin hareket ettirici kuvveti tükenir ve doğal hareket yapmaya başlar.

1540’larda fırlatılan bir cismin her zaman eğri bir yol izlediğini gözlemleyen İtalyan fizikçi Niccolo Tartaglia (1500-1557), bir merminin 45 derecelik eğik atışla fırlatıldığında en uzak mesafeyi kat edebileceği görüşünü ortaya atmıştı (Tez, 1995: 77). Hareketin bağımsızlığı ve eylemsizlik ilkesine dayanan Galileo ise Discorsi’de fırlatılan bir merminin düzgün doğrusal hareket ile serbest düşme hareketinin bileşkesi olan parabol biçiminde bir yörünge izlediğini gösterdi:

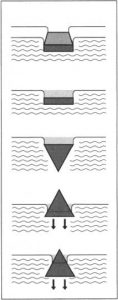
“Sürtünmenin olmadığı yatay bir düzlem boyunca fırlatılan herhangi bir parçacık imgeleyelim…bu parçacık, düzlemin sınırı olmaması koşuluyla, bu aynı düzlem boyunca eş biçimli ve sürekli olan bir devinimle devinecektir. Ama eğer düzlem sınırlıysa ve yükseltiliyse ağır olduğunu imgelediğimiz devinen parçacık, düzlemin sınırını geçmesi üzerine, önceki eş biçimli ve sürekli devinimine ek olarak kendi ağırlığından ötürü aşağıya doğru bir eğilim kazanacaktır; böylece fırlatma [projectio] dediğim bileşke, devinim bir eş biçimli ve yatay devinim ile dikey ve doğal olarak ivmelenen bir başka devinimden oluşur…Doğal olarak ivmelenen dikey bir devinimle bileşmiş eş biçimli yatay bir devinim ile ilerleyen fırlatılan cisimlerin betimlediği yol bir yarım paraboldür.” (Galileo, 2011: 223)

Görüldüğü gibi fırlatılan cisim her an yatay bir çizgi üzerinde sabit bir hızla yani eylemsizlik ilkesine göre hareket eder ve aynı zamanda düşey olarak düşme hareketine yani düzgün ivmeli harekete sahiptir. Fırlatılan bir cismin izlediği yol iki hareketin bileşimidir. Bu iki hareket birbirini engellemez ve bu iki hareketin geometrik kesiti bize bir parabol verir. Böylece, Ortaçağ Aristoteles fiziğinde ileri sürülmüş olduğu gibi fırlatılan bir cismin düz değil parabolik bir yol izlediği görüşü Galileo tarafından kullanılmış oluyordu.

Galileo’nun fizik bilimine yapmış olduğu başlıca katkılar şöyle özetlenebilir: Düşen bir cismin hareketi kanunu; fırlatılan bir cismin, parabolik bir yörünge üzerinde hareket etmesi; cisimlerin ağırlıklarına ve kendilerini meydana getiren elemanların özelliklerine bağlı olmadan boşlukta aynı hızla düşmesi; eğik bir düzlem üzerinde düşen ya da yuvarlanan bir cismin sabit bir ivmeyle bu düşme hareketini sürdürmesi.

Eylemsizlik ilkesi ve Copernicus sistemi
İlk kez Galileo tarafından gündeme getirilen eylemsizlik ilkesi astronomide Copernicus’un güneş-merkezli sistemini destekleyen bir fizik kuralı olarak işledi. O dönemde güneş-merkezli evren modelinin yol açtığı bazı sorulara henüz cevap verilemiyor ve bu yüzden birçok gökbilimci Copernicus sistemine karşı çıkıyordu. Bu gökbilimcilerden biri de Tycho Brahe’dir. Brahe, kulenin tepesinden bırakılan bir cismin kulenin dibine düşmesini örnek göstererek güneş-merkezli evren modelini eleştirdi. Döneminin birçok gökbilimcisi gibi Brahe de şöyle akıl yürütüyordu: Eğer Dünya Copernicus sisteminin öngördüğü gibi kendi etrafında dönüyor, yani hareket ediyorsa kulenin tepesinden bırakılan taşın kulenin dibine düşmemesi gerekir. Çünkü taş kuleden düşerken kule Dünya ile birlikte hareket edeceği için, kule taştan uzaklaşır. Taşın bu şekilde geride kalması, kulenin batısında bir noktaya düşmesi demektir. İşte Galileo’nun ortaya attığı eylemsizlik ilkesi bu tür karşı çıkışları geçersiz kıldı.

Eylemsizlik ilkesi gereğince kulenin tepesinden bırakılan bir cisim, düşme hareketinin yanı sıra Yer’in ve kulenin hareketini de paylaşır, yani yatay doğrultudaki hareketine devam eder. Fakat bu yatay hareket gözlenemediği için cismin gözlenen hareketi kulenin tepesi ile dibi arasındaki düşey bir çizgi doğrultusunda olur. Yani eylemsizlik ilkesi, Copernicus sistemiyle uyum içinde olan bir fiziğin kurulmasına dayanak sağlıyordu.

Galileo’nun eylemsizlik ilkesi gereğince gerçekleşen hareket doğrusal değil, dairesel bir hareketti. Ancak bu durum, çelişkili gibi görünse de Galileo’nun Copernicus sistemini savunmasını kolaylaştırıcı bir etki yapmıştır. Çünkü onun Copernicus sistemini savunabilmek için dairesel hareketlere ihtiyacı vardı. Eğer Galileo bilimsel açıdan daha doğru olan düzgün doğrusal hareket görüşünü savunmuş olsaydı Ay’ın ya da gezegenlerin dairesel hareketlerini, teorisinin bütünlüğü içinde açıklamakta çok zorlanacaktı. Yani Ay’ın ya da gezegenlerin dairesel hareketini düzgün doğrusal hareket ile düşme hareketinin bir bileşkesi olarak tanımlaması olanaksızdı. Bu tanımlama, daha sonra, evrensel çekim ilkesini matematiksel olarak formüle eden Isaac Newton tarafından yapılacaktır.

Teleskop: Devrimi hızlandıran alet
Kepler’in Brahe’nin gökbilimsel gözlemlerine dayanarak hazırladığı Rudolphine Tables adlı çizelgesinin, 1627 yılında yayınlanmasından sonra, Copernicusçu gökbilimcilerin sayısı artmaya başladı. Aslında Kepler’in yaptığı çalışmaların diğer gökbilimcilerce kabul edilmesi Copernicus devriminin astronomideki başarısı için yeterliydi. Diğer bir deyişle Galileo ile aynı dönemde yaşayan Kepler’in çalışması astronomide kalıcı olması için gerekli tüm öğeleri içeriyordu. Galileo’nun teleskopu gökbilimsel amaçlarla kullanmaya başlaması ise -göksel gizemi çözümü kolay bir bilmeceye dönüştürerek- astronomi devrimini hızlandırdı:

“Galileo Galilei eskiçağdan bu yana ilk kez farklı nitelikte yeni verilerle astronomiye katkıda bulunuyordu. Galileo’nun teleskopu göklerin astronomlara sunduğu bilmeceyi değiştirmişti; teleskop Galileo’nun elinde Copernicusçuluğu destekleyen sayısız kanıt ortaya çıkardığı için, bilmecenin çözümünü çok kolaylaştırıyordu. Galileo’nun değiştirdiği bilmece, ancak farklı yollardan çözüldükten sonra dile getirilir. Daha önce ortaya konmuş olsaydı, Copernicus Devriminin öyküsü farklı olabilirdi. Zamanlaması açısından bakıldığında, Galileo’nun astronomi üzerine yaptığı çalışma, Copernicus Devriminin zafer kazanacağı açıkça görüldükten sonra yürütülen süpürme harekâtına katkıda bulunmuştur.” (Kuhn, 2007: 355)

Teleskopu ilk yapan ve kullanan kişi Galileo değildi. İnce kenarlı (dışbükey) mercekler 1300’lerden beri İtalya’da biliniyor ve yakını göremeyenler için gözlük yapımında kullanılıyordu. Kalın kenarlı (içbükey) mercekler ise uzaktaki nesneleri iyi seçemeyenler için 1450 civarında yapılmaya ve kullanılmaya başlandı. Hollandalı mercek yapımcısı olan Hans Lipperhey, 1608 yılında, dışbükey ve içbükey mercekleri bir boru içinde birleştirerek uzaktaki cisimleri üç ya da dört kat büyük gösteren bir alet yaptı. Aynı tarihlerde diğer optikçiler de bu tür bir alet yaptılar. Teleskopu ilk yapanlardan biri de Jacop Metius adlı bir Hollandalıdır. Teleskopun deniz taşımacılığında ve askeri işlerdeki önemi hemen anlaşıldı ve kullanılmaya başlandı. Bu icadın haberini 1609 yılının yazında alan Galileo aynı yılın Kasım sonuna gelindiğinde büyütme gücü 20 olan bir teleskop yapmayı başarmıştı:

“Galileo teleskopun ucunda daha ince bir dışbükey mercek kullanarak bu Hollanda tasarımını geliştirdi; böylece yaklaşık 120 santimetre daha uzun bir odak uzaklığı elde etti. Teleskopun gözle bakılan ucunda da çok daha güçlü (odak uzaklığı daha kısa olan) içbükey mercek kullandı. Bu değişikliklerin her ikisi de büyütmeyi artırdı. Galileo keşiflerini yaklaşık 20 büyütme gücündeki bir teleskopla yaptı. Bu tür teleskoplar en fazla yaklaşık 30 büyütme gücünde olabilir.” (MacLachan, 2008: 48)

Başlangıçta mali durumunu düzeltecek bir araç olarak gördüğü teleskopu gökyüzüne çeviren Galileo, büyük bir şaşkınlık yaşadı. Nereye baksa o zamana kadar bilinenin on katı daha fazla yıldız görüyordu. Samanyolu’nun sisli bir kuşak değil binlerce yıldız içeren kümelerden oluştuğunu anladı. Galileo teleskopla yaptığı gözlemlerin bazı sonuçlarını, gökbilimle ilgili şu yapıtlarında topladı: Sidereus Nuncius (Yıldız Habercisi, 1610), Istoria e dimostrazioni intorno alle macchie solari e loro accidenti (Güneş Lekelerinin Tarihi ve Kanıtları, 1613), Discorso Delle Comete (Kuyruklu Yıldızlar Üzerine Bir Söyleşi, 1619), Il Saggiatore (Ayarcı, 1623). Bu son yapıt Cizvit matematikçi Orazio Grassi’nin Galileo’nun gözlem ve yorumlarına saldırdığı Libra astronomica e filosofica (Gökbilimsel Denge) adlı metnine bir cevaptır. Galileo, Grassi’nin denge benzetmesini sürdürerek kitabına Ayarcı adını vermiştir. Galileo’nun bu gözlem ve keşifleri şu başlıklar altında toplanabilir: Samanyolu ve sabit yıldızlar, yıldızların açısal çapları, Ay yüzeyindeki şekiller, Güneş lekeleri, Jüpiter’in uyduları, Satürn’ün halkaları, Venüs’ün evreleri.

Galileo ilk gözlemlerini ve radikal görüşlerini kamuoyuyla paylaşmaya başladığında fikrini ve desteğini almak için Kepler’e Yıldız Habercisi adlı yapıtıyla birlikte bir mektup gönderdi. Kepler ise bu mektubu kısa sürede 35 sayfalık bir mektupla yanıtladı ve bunu, pek çok insan mektupta yazılanları merak ettiğinden, Dissertatio Cum Nunceo Sidereo (Yıldız Habercisiyle Sohbet, 1610) başlığıyla küçük bir kitap olarak yayınladı. Galileo’nun gözlemlerinden etkilenen Kepler hem Galileo’yu desteklemek hem de kendi gözlemlerini yapabilmek için Dioptrice (Kırılma, 1611) adlı yapıtında iki mercekli sistemlerle ilgili ilk detaylı optik teorisini geliştirdi. Bu yapıtta, günümüzde “Kepler teleskopu” olarak isimlendirilen iki dışbükey merceğin kullanıldığı bir teleskop tasarımı da bulunuyordu.

Galileo, teleskopla daha önce çıplak gözle görünmeyen yeni yıldızlar gözlemledi. Örneğin daha önce Orion takımyıldızında dokuz yıldız gözlemlenirken aynı takımyıldızda seksen yıldız saydı. Astronomide teleskopun kullanılmadığı dönemlerde Samanyolu ve kuyrukluyıldızların Dünya ile Ay arasında (yani ayaltı dünyada) bir gök olayı olduğuna inanılıyordu. Oysa Samanyolu’na teleskopla bakıldığında sonsuz sayıda yıldızlar topluluğu olduğu anlaşılıyordu.

“Her gece sayısız yeni cisim keşfedilen gökler kalabalıklaşıyordu. Kimi Copernicusçuların savunduğu geniş, hatta sonsuz evren varsayımı birdenbire daha akla yakın bir varsayım olarak görülmeye başlandı. Bruno’nun, sınırsız bir uzama yayılan ve sonsuz sayıda cisim barındıran evrenin, Tanrı’nın sonsuz üretkenliğini gösterdiğine ilişkin gizemci görüşü neredeyse elle tutulur, gözle görülür bir şey olmuştu.” (Kuhn, 2007: 356)

Aslında evrenin çok geniş olduğu görüşüne yol açan şey teleskopla yapılan gözlemlerden çok Galileo’nun yorumlarıydı. Örneğin yeni gözlenen yıldızların diğerlerinden daha küçük görünmelerini Galileo “diğer yıldızlarla aynı uzaklıkta ama onlardan daha küçük oldukları” yorumuyla değil “diğer yıldızlarla aynı büyüklükte ama daha uzakta oldukları” yorumuyla açıklamayı tercih ediyordu. Galileo’nun bu yorumları evrenin daha da geniş olarak tasarlanmasına yol açtı. Copernicus sisteminin eskisine oranla daha büyük bir evren kavramını gerektirmesi de Galileo’nun söz konusu yorumları yapmasında etkili oldu.

Brahe’nin Copernicus sistemine yönelttiği eleştirilerden biri de yıldızların büyüklüğüne yönelikti. Ptolemaios sisteminde sabit yıldızların büyüklüğünün yaklaşık Güneş kadar olduğu düşünülüyordu ve bu akla yakındı. Eğer Copernicusçu evren, yıldız paralaksının gerektirdiği ölçüde büyükse, yıldızlar inanılmaz boyutlarda olmalıydı. Brahe’nin hesaplarına göre parlak bir yıldızın yarıçapı Güneş ile Dünya arasındaki uzaklığa (ya da çapı Yer’in yörüngesine) eşit olacak denli büyük olmalıydı ve bu sonuç kabul edilemezdi.

“Ancak, teleskop göklere doğrultulduğunda, Brahe’nin sorununun yalnızca görünüşte bir sorun olduğu anlaşıldı. Yıldızların onun tahmin ettiği ölçüde büyük olması gerekmiyordu. Teleskop göklerde gözlenebilen yıldızların sayısını fazlasıyla artırmış, ancak görünüşteki boyutlarını artırmamıştı. Galileo’nun teleskopuyla büyüyen Güneş, Ay ve gezegenlerin aksine, yıldızların boyutlarında bir değişiklik olmamıştı. Böylece yıldızların açısal çapının çıplak gözle yapılan gözlemlerde fazlasıyla abartılmış olduğu açığa çıkıyordu” (Kuhn, 2007: 357).

Bu gözlemlerle kanıtlanıyordu ki Copernicus sistemi doğru kabul edildiğinde de yıldızların büyüklüğü kabul edilebilir boyutlarda kalıyordu. Böylece, Copernicus sistemine yöneltilen eleştirilerden biri daha çöküyordu.

Copernicusçuluğu destekleyen gözlemler sadece yıldızlardan gelmiyordu. Galileo teleskopunu Ay’a çevirdiğinde, yeryüzüne çok benzer bir görünüm sergilediğini fark etti:

“Ay’ın yüzeyinin çukurlar, kraterler, vadiler ve dağlarla kaplı olduğunu gördü. Güneş, Ay ve Yer’in göreli konumlarının bilindiği bir zamanda dağların kraterlere düşen gölgelerinin uzunluğunu ölçerek eğimli bölgelerin derinliklerini, tümseklerin yüksekliğini hesapladı ve Ay’ın üç boyutlu topografyasını çıkarmaya başladı.” (Kuhn, 2007: 358)

Ay’ın topografyasının Yer’in topografyasından farklı olamadığı sonucuna ulaşan Galileo Ay’la Dünya arasındaki benzerliği kullanarak Yer’in hareketine karşı yöneltilen eleştirilere cevap verdi. “Ay da tıpkı dünya gibi büyük, ağır ve hareket eden bir küredir. Ay’ın uzaydaki hareketine hiç kimsenin itiraz etmediği halde, Yer’in uzaydaki hareketine neden karşı çıkılmaktadır?” Ay gözlemleri Galileo’ya Copernicusçu astronomiyi savunması için yeni araçlar sağladı.

Bir Alman gökbilimci ve Cizvit olan Christoph Scheiner (1573-1650) teleskopuyla Güneş lekelerini gözlemledi ve bunu 1612 yılında bir kitapçık olarak yayınladı.

“Bu lekeler, Güneş’in kusursuz bir cisim olduğuna inanan Aristotelesçilere büyük sıkıntı yaratı. Scheiner lekelerin aslında Güneş’in yüzeyinde olmadığını ileri sürüyordu. Çok sayıda küçük yıldızdan oluşan kümeler Güneş’in etrafında dönüyor ve Güneş’in önünden geçerken görünür hale geliyorlardı.” (MacLachan, 2008: 48)

Bu lekeleri daha önce gözlemlemiş ama konu üzerinde fazla durmamış olan Galileo Scheiner’in kitapçığından sonra teleskopunu yeniden Güneş’e çevirdi. Güneş yüzeyinde hareket eden küçük siyah lekeler için Scheiner’den faklı olarak “Güneş kendi ekseni etrafında döndüğü için lekeler de hareket halindedir” yorumunu getirdi ve Güneş’in kendi ekseni etrafındaki dönüşünü bir aydan daha kısa bir sürede tamamladığı sonucuna ulaştı. Güneş’in kendi ekseni etrafında dönüyor olması Yer’in dönüyor olma olasılığını gündeme getiriyordu. Yani Galileo, yapmış olduğu gözlemleri, Copernicusçuluğu destekleyen tarzda yorumlamaya devam etti.

Galileo, Jüpiter’in etrafında, önce yıldız olduğunu zannettiği dört gökcismi fark etti. Jüpiter hareket ettiğinde o yıldızlar da Jüpiter’le birlikte hareket ediyorlardı ve ayrıca bu dört yıldız birbirlerine göre de yerlerini değiştiriyorlardı. Galileo’ya göre onlar Jüpiter’in etrafında dolanan uydulardı. Ptolemaios sisteminde Ay bir gezegen olarak ele alınırken, Copernicus sisteminde Yer’in çevresinde dolandığı düşünülerek bir uydu olarak kabul edilir. Ancak Copernicus sisteminde Ay, başka bir uydunun varlığı bilinmediği için tek uydu olarak kalmıştı. Bu durum Copernicusçulara, “Bütün gök cisimleri Güneş etrafında döndükleri halde Ay neden Yer’in etrafında dolanmaktadır?” ya da “Ay neden özel bir cisimdir?” gibi soruların yöneltilmesine yol açıyordu (Akdoğan, 1996: 96; Westfall, 1995: 13; Vigoureux, 2008: 196). Jüpiter’in dört uydusunu kefeden Galileo ise Ay’ın evrende var olan tek uydu olmadığını kanıtlamıştı. Jüpiter’in uydularının keşfedilmesi sonucunda gökbilimciler “gezegenlerin güdücü etkisi altındaki uyduların varlığını kabul etmek zorunda” kalıyorlardı. Jüpiter’in uydularının keşfedilmesinin belki de en önemli sonucu, Copernicus sisteminin görsel bir modelini oluşturmuş olmasıydı.

Galileo, teleskopuyla Satürn’ü ve halkalarını da inceliyordu. Ancak kullandığı teleskopun büyütme gücü halkaları net olarak gösterecek kadar yüksek değildi. Bu nedenle Galileo’nun Satürn çizimleri gezegenin iki yanında kulakları varmış gibi görünüyordu. Halkaların dönmediğini düşünüyor ve bunlardan “Satürn’ün eşlikçileri” olarak söz ediyordu. Satürn’ün etrafındaki halkalar hakkında daha geniş bilgi, 1656 yılında Christian Huygens tarafından daha gelişmiş bir teleskop ile yapılan gözlemler sayesinde elde edilmiştir.

Teleskopla yapılan gözlemler Copernicus sistemi lehine çok sayıda kanıt ortaya koymuş olsa da doğrudan doğruya en etkili kanıtlar Venüs gözlemlerinden gelmiştir. Ptolemaios sisteminde Venüs’ün Güneş’le Yer arasında bir episaykıl üzerinde döndüğü kabul ediliyordu. Bu nedenle Venüs’ün dünyadan görünüşünün “her zaman için küçük bir hilal” şeklinde olacağına inanılıyordu. Copernicus De Revolutionibus’unda, “eğer ayrıntılı gözlenebilirse, Venüs’ün görüntüsünün bu gezegenin yörüngesinin biçimi konusunda dolaysız bilgi verebileceğini belirtiyordu.” (Kuhn, 2007: 359-360) Ancak çıplak gözle Venüs’ün evrelerini fark etmek son derece zor olduğu için böyle bir gözlem gerçekleştirilemiyordu. Teleskopun gezegenlerin görüntüsünü yeteri kadar büyütmesi Venüs’ün gözlenmesine de olanak sağlamıştır.

“Venüs hilal şekline büründükçe, görünür çapı büyüdü. Galileo bunun Venüs’ün Dünya’ya yaklaştığı anlamına geldiğini kavradı. Venüs küçük ve neredeyse tam yuvarlakken Güneş’ten daha uzaktaydı, daha büyük ve hilal şeklindeyken ise Güneş’ten daha yakındı. Bu gözlemler Galileo’yu Venüs’ün Copernicus sisteminde tarif edildiği gibi Güneş’in yörüngesinde döndüğüne ikna etti. İlk defa Copernicus’u destekleyebilecek nitelikte güçlü görsel kanıtları olduğunu hissediyordu.” (MacLachan, 2008: 57)

Galileo’nun teleskopla Venüs’ün evrelerini gözlemlemesi bir bakıma Ptolemaios sisteminin yanlışlığını ve Copernicus sisteminin doğruluğunu ortaya koyuyordu. Çünkü Venüs’ün evreleri, eğer Venüs Copernicus sisteminin varsaydığı gibi Güneş’in etrafında dönüyorsa oluşabilirdi. Ancak bir bakıma da Copernicus sistemini tam olarak doğrulamış olmuyordu. Çünkü Venüs’ün Güneş etrafında dönmesi ve evreleri, Pontuslu Heraclides’in ve Brahe’nin astronomi sistemlerine de uygun düşmekteydi. Ne var ki Galileo söz konusu sistemleri görmezlikten gelmiş ve Venüs’ün evreleri ile uyum içinde olanın yalnızca Copernicus sistemi olduğunu ileri sürmüştür.

Aslında Galileo’nun astronomi alanındaki çalışmaları, Copernicusçu bir gözle yorumladığı gözlem ve keşiflerle sınırlı kalmış ve matematiksel değil gözlemsel astronomiye katkıda bulunmuştur. Ne yazık ki matematiksel astronomide çok önemli gelişmeye imzasını atan Kepler’in eliptik yörünge fikrini kabul etmemiş olan Galileo’ya göre gezegenler Güneş’in etrafında dairesel yörüngelerinde dönmeye devam etmişlerdir. Einstein şöyle yazar: “Kepler’in ortaya koyduğu kesin ilerlemenin Galileo’nun eserleri üzerinde hiçbir iz bırakmamış olması, yaratıcı zekâların genellikle birbirlerinden hiçbir biçimde yararlanmadıklarının; birbirlerinden bir şey almaya yanaşmadıklarının çarpıcı bir örneğini sunar.” (Vigoureux, 2008: 124)

Gözlemlere ve teleskopa karşı çıkışlar
Galileo’nun teleskopla yaptığı gözlemler Copernicus’un kavramsal sistemine güçlü görsel kanıtlar sağladığı halde tam olarak kanıtlamaktan uzaktı. Ancak bu gözlemler Galileo ve diğer Copernicusçular tarafından geleneksel Aristoteles-Ptolemaios sistemini savunanlara karşı çok etkili silahlar olarak kullanılmıştır. Bu mücadelede söz konusu olan kanıtlamadan ziyade propagandaydı (Kuhn, 2007: 361). Yani gözlemlerin nasıl yorumlanacağı, yani hangi sistem içinde anlamlandırılacağı konusunda bir savaş vardı.

Galileo teleskopla yaptığı gözlemlerini Copernicusçu bir paradigma içinde yorumluyor, bu yorumlardan da göklerin mükemmel olmadığı sonucu çıkıyordu. Ayüstü dünya da tıpkı ayaltı dünya gibi mükemmel değildi. Bu durumda Yer de sıradan bir gezegen olarak kabul edilebilirdi.

Galileo’nun yorumlarını kabul ettirmesi kolay olmamıştır. O sırada Prag’da yaşayan ve Jüpiter’in uydularını teleskopla gözlemleyerek bir kitapçık yazan Kepler dışında önemli bir desteği yoktu. Aristotelesçi filozoflar gökyüzünün mükemmel olduğunu ısrarla savunmaya devam ediyorlardı. Özellikle Ay yüzeyinin pürüzlü ya da engebeli olduğu görüşüne karşı çıkıyorlardı. Bu filozoflardan biri Floransa’da yaşayan Ludovico delle Colombe göklerin kusursuzluğunu savunan kitabında, önceden gözlenmemiş parlak bir yıldızın (yani bir ‘süpernova’nın) artık gözlenebilir olmasını “gökyüzünde hareket eden [ve kendisi görünmez olan] bir tür merceğin onu insan gözüne görünür hale getirmesiyle” açıklamaya çalışmıştı (MacLachan, 2008: 39). Colombe aynı zengin hayal gücünü Ay’ın pürüzsüz olduğunu savunmakta da kullanmıştır: “Colombe Ay’ın karanlık yüzeyinin pürüzlü olabileceğini, ancak görülemeyen ve tamamen pürüzsüz bir yüzeye sahip kristal bir maddeyle kaplı olduğunu ileri sürüyordu.” (MacLachan, 2008: 55-56) Ay yüzeyinin engebeli olduğu fikrini kabul edemeyenlerden biri de Cizvitlerin başlıca eğitim merkezi olan Roma Koleji’nin matematik bölümü dekanı Christoph Clavius’tu. Bir teleskop yardımıyla Clavius ve Cizvit arkadaşları Galileo’nun tüm gözlemlerini doğrulamışlardı:

“Gözlemlere ilişkin bir itirazı olmamasına rağmen Clavius’un yorumları Galileo’nunkilerden farklıydı. Clavius Aristoteles’in fikirlerine sıkı sıkıya bağlıydı. Ay’ın yüzeyinin engebeli olduğu fikrini kabul edemiyordu. Ay’ın pürüzsüz yüzeyinin farklı yoğunlukları olan bölgelerden meydana geldiğini düşünüyordu. Anlaşıldığı kadarıyla Galileo’nun değişen parlak ve karanlık lekelerle ilgili savı Clavius’a inandırıcı gelmemişti.” (MacLachan, 2008: 59)

Galileo’nun gözlem ve yorumları teleskopun güvenilirliği de gündeme getirmişti. O sıralarda bir teleskop edinen Kepler bu aletin “kralların asasından çok daha değerli” (Sobel, 2000: 44) olduğu yargısına ulaşmış olsa da bazı bilimciler teleskopun astronomide güvenilir bir alet olmadığına inanıyorlardı. Örneğin Clavius, “teleskoptan görünen bütün yeni şeylerin gökyüzünde değil (teleskopun) merceklerinde” (Drake, 1989: 44) olduğunu söylemişti. Bu davranış aslında optik aletlere karşı yaygın bir güvensizliğin ifadesiydi. Çünkü o dönemde büyücüler ve bazı sıradan hokkabazlar da insanları kandırmak için aynalardan ve merceklerden oluşan düzenekler kullanıyorlardı (Henry, 2009: 6; Vigoureux, 2008: 198). Gözün en güvenilir gözlem aracı olduğu varsayılıyor ve “eğer gerekseydi tanrı insanlara zaten teleskop biçiminde gözler verirdi” biçiminde düşünülüyordu. Geleneksel yaklaşımın sağlam zemininden ayrılmak istemeyen gökbilimciler ve filozoflar önce teleskoptan bakmayı reddediyorlar, baktıklarında da bu yeni gözlenen cisimlerin gökyüzünde değil teleskopun içinde olduğunu ileri sürüyorlardı. Fakat bir süre sonra bu yeni cisimleri kendi gözleriyle gördükçe karşı çıkışlar da azaldı.

Günümüzün standartlarına göre sıradan bir dürbün olan ‘teleskop’ için Galileo Sidereus Nuncius (1610) adlı yapıtında perspicilli ismini kullanıyordu. Latince perspicio: içinden bakmak ya da görmek; perpicuus: saydam, duru anlamına gelir. ‘Teleskop’ kelimesi ise, daha sonra Roma’da Federico Cesi’nin başkanı olduğu Lincean Akademisi’nin bir toplantısında, konuklar arasında bulunan Yunanlı matematikçi Giovanni Demisiani’nin önerisiyle icat edilmiştir:

“14 Nisan 1611’de Prens Cesi Galileo’yu bir ziyafete davet etti. Bilimadamının diğer konuklara teleskopun kullanımını göstermesini istiyordu. Galileo’nun yeni aygıtı için telescopium adı işte bu toplantıda ortaya atılmıştır. Bu Latince sözcüğün kökleri Yunancada ‘uzakta’ anlamına gelen tele ve ‘bakmak’ anlamına gelen scopein’den geliyordu, yani uzağa bakmak için bir aygıt. Yeni sözcük kısa süre içinde İngilizcede telescope, İtalyancada telescopio olarak kabul edildi.” (MacLachan, 2008: 60)

Koyré’ye göre Galileo’nun teleskopu yalnızca “Hollanda dürbünü”nün gelişmişi değildir; bir optik teoriden yola çıkılarak yapılmıştır (Koyré, 1994: 52). Ancak o dönemde teleskopun güvenilir bir gözlem aracı olduğunu gösterecek bütünlüklü bir teorik açıklamasının olmayışı teleskopla yapılan gözlemleri tartışmalı kılan ve yapılan keşiflerin etkisini azaltan bir öğe olmuştur. Çünkü farklı maddelerden oluştuğu ve farklı yasaların geçerli olduğu kabul edilen ayaltı ve ayüstü dünyalardaki nesnelerin gözlenmesinin aynı doğrulukta olmayacağı düşünülüyordu. Bu görüşe göre teleskop, “duyumlarımız yakınımızdaki yersel nesnelerin görünüşlerine alışık olduğu” için, yeryüzündeki nesneleri “seçik olarak algılayabilir.” Ancak yıldızlar hiçbir zaman yakından algılanmamış oldukları için, “teleskoptan gelen etkilerle, nesnenin kendisinden çıkan etkileri” (Feyerabend, 1991: 133) ayırmak gerekliliği ortaya çıkar.

 Galileo ve Kilise
Galileo’nun yargılanması bilim tarihinin en tartışmalı konuları arasında yer alır. Bu olay bir açıdan bilim ve din arasındaki özsel karşıtlığın bir cisimleşmesi olarak görülürken, başka bir açıdan bir dizi rastlantının ya da seçimin bir araya gelmesinin zorunlu bir sonucu olarak değerlendirilir.

Copernicus sistemini benimsemiş Galileo’nun mahkûmiyetiyle sonuçlanan süreç Aristotelesçi filozofların dinsel saldırısıyla başlamıştı: Yer’in hareket ettiği görüşü Kitab-ı Mukaddes’le çelişmez miydi? Galileo’nun muhalifleri Dünya’nın hareketsiz durduğu ve Güneş’in döndüğü iddiasının kanıtı olarak Kitab-ı Mukaddes’in Yaratılış 1’i, Derlemeci l :4-6’yı, Yeşu 10:12’yi, Zebur 19:4-6, 93 ve 104’ü sık sık alıntılamışlardır (Blackwell, 2016: 143). En çok alıntı yapılan metindeki ifadeler açıktı:

“Dur, ey Güneş, Gibeon üzerinde; ve Ay, sen Ayyalon deresinde. (…) Güneş durdu ve Ay yerinde kaldı. (…)Ve Güneş göklerin ortasında durdu ve tam bir gün kadar batmakta acele etmedi.” (Yeşu’nun Kitabı, 10: 12-14)

Galileo saldırının özellikle kendisini hedeflediğini düşünmemiş ama felsefeyle Kitab-ı Mukaddes’in, yani bilim ve dinin karşı karşıya getirilmesinden kaygılandığı için, uzun bir mektup yazarak tarafları uyarmıştı: “Kutsal metinlerin amacı bize nasıl cennetlik olunacağını söylemektir, cennetin nasıl olduğunu değil.” (Sobel, 2000: 66; MacLachan, 2008: 88) Bunun anlamı açıktır: Teologların otoritesi ahlaki alanda geçerliyken felsefecilerin işi cennet ya da gökyüzü dâhil doğayı araştırmak olmalıdır. Ancak aklın ve bilimin bu özerklik talebi Kilise açısından potansiyel bir tehlikeydi. Akıl bir alanda serbest bırakılırsa ahlakın ve inancın bulunduğu diğer alanları da kontrol etmeye yönelebilirdi. Galileo’nun amacı doğa felsefesine,  yani fizik bilimine yer açmaktı. O daha yirmi dört yaşındayken Dante’nin Cehenneminin Biçimi, Yeri ve Boyutuyla İlgili Dersler’i (Galileo, 2009) kaleme alarak bu yönelimini belli etmişti. Galileo evrenin fiziksel yapısıyla ilgiliydi.

Doğa kitabı
Galileo da her inançlı Hıristiyan gibi evrenin Tanrı tarafından yaratıldığına ve Kitab-ı Mukaddes’in güvenilir bir bilgi kaynağı olduğuna inanıyordu. Ancak Kitab-ı Mukaddes tek bilgi kaynağı değildi. Onun kadar önemli bir bilgi kaynağı olan “doğa”, Tanrı’nın ikinci kitabıydı. Kitab-ı Mukaddes’in kendisi de doğanın bir bilgi kaynağı olduğunu kabul etmekteydi. Hem kutsal kitabı hem de doğa kitabını Tanrı yazmış olduğundan her ikisi de eşit ölçüde doğruydu ve çelişmeleri mümkün değildi. Bununla birlikte, Galileo’ya göre bilimin bir üstünlüğü vardı: “Doğayla ilgili konularda Yaratıcının gözle görünen eserine kıyasla kutsal metinlerin daha az açık olduğu” (Galileo’dan akt. Vigoureux, 2008: 207) söylenebilirdi. Çünkü kutsal kitabın dili yer yer herkesin anlayabileceği biçime sokulmuştu. Bu kısımlar kelimesi kelimesine okunmamalı, alegorik ya da simgesel okumalardan yardım alınmalıydı. Galileo’nun sözleriyle:

“Kitab-ı Mukaddes’in yanılması olanaksızdır; içindeki hükümler mutlak olarak doğrudur ve aksi kanıtlanamaz. Ben buna sadece şunu ekledim: Kitab-ı Mukaddes’in yanılmaz olmasına karşın, onun tefsircileri, daima kelimelerin lâfzî anlamlarına dayanacaklarından, pek çok bakımdan yanılmaya müsaittirler. O yüzden, bu yaklaşım tarzında, pek çok çelişkinin yanı sıra, vahim sapkınlıklar ve küfürler de kendini gösterecektir; zira bu durumda Tanrı’ya el, ayak ve gözle birlikte, öfke, pişmanlık, nefret ve geçmiş konusunda zaman zaman unutkanlık, geleceği ihmal gibi insani ve bedensel zaaflar yakıştırmak gerekecektir.” (Sobel, 2000: 64)

Kitab-ı Mukaddes’te yer alan Yer’in hareketsiz olduğu biçimindeki ifadenin nedeni de aslında insanların gündelik deneyimleriydi. Bu yüzden Kitab-ı Mukaddes’te doğal olayları anlatmak için kullanılan dil, içinde örneğin primum mobile (Aristoteles-Ptolemaios evren sisteminde “ilk hareket ettirici”) kavramının geçtiği felsefi (bilimsel) bir dil olamazdı. Dolayısıyla doğa kitabını okuyabilen felsefeciler, sadece kutsal kitabı okuyabilen teologlardan üstündü. Yani doğa felsefecileri Kitab-ı Mukaddes’teki sözleri anlama konusunda din adamlarından daha iyi bir konumdaydılar. Galileo’nun sözleriyle:

“Duyusal deneyimle gözlerimizin önüne konan ya da gerekli kanıtların bize gösterdiği fiziksel hiçbir şeyin, kelimelerin ötesinde bazı farklı anlamları da içinde taşıyabilecek Kitab-ı Mukaddes pasajlarının tanıklığında sorgulanmaması gerekir. Fizikte herhangi bir kesinliğe ulaştığımızda, bunları Kitab-ı Mukaddes’in doğru açıklamasında en uygun yardımcılar olarak bir araya getirmeliyiz.” (Trusted, 1994: 55)

Sapkın Galileo?
Maddenin içsel yapısı konusunda “atomcu” bir görüşü benimsemiş olan Galileo, bu bağlamda materyalistti. H. Martin, P. Redondi, P. Costabel, I. Stengers ve P. Thuillier gibi kimi bilim tarihçileri Galileo’nun yargılanmasına giden sürecin asıl ve gizli nedeni olarak onun materyalist yaklaşımını gösterirler. Onun materyalizmi kutsal şarap ve ekmeğin İsa’nın kanına ve bedenine dönüşebileceğini varsayan ökaristik mucizeyi tehdit etmekteydi (Vigoureux, 2008: 216-217). Bu görüşe göre asıl yargılanan eser 1632 tarihli Dialogo değil 1623 tarihli Il Saggiatore’dir. Pietro Redondi, Sapkın Galileo adlı kitabında bu tezi geniş bir biçimde işlemiştir.

Ökaristik tözsel dönüşüm (Eucharistic transubstantiation. Eucharist: Hıristiyanlıkta kurban ya da sunu istemeyen Tanrı’ya şükretmek için kutsal ekmek ve şarabın ritüel paylaşılması; Efkaristiya.) dogmasına göre İsa’nın eti ve kanı ekmek ve şaraba dönüşmekteydi. Aristotelesçi töz ve ilinek kavramları arasında kurulan ilişki de bu dogmaya metafizik bir temel sağlamaktaydı. Buna göre biz tat, biçim, koku gibi ilinekleri algılayabiliriz ama tözü algılayamayız. Dolayısıyla aynı ilineklerin altında farklı tözlerle karşılaşabiliriz. Aristoteles’in doğa felsefesi, başka şeylerle birlikte, ökaristik mucizeyi onaylamaya yarıyordu. Bu durumda ayin ekmeği, görüntüsü değişmediği halde İsa’nın etine dönüşebilir ya da dindar bir Hıristiyan, komşusunun suretinde şeytanı görebilirdi.

Galileo felsefenin, yani bilimin doğası konusunda oldukça modern bir tutum geliştirmiştir. Aristotelesçiler felsefenin gerçeğin özünü yakaladığını düşünürler; yani tözün bilgisi mümkündür. Galileo için ise, tözün bilgisine değil, ancak ilineklerin bilgisine erişilebilir. Bu ilinekler de Galileo’nun “birincil nitelikler” olarak adlandırdığı özelliklerdir (Minois, 2010: 58). Yani Aristotelesçi anlamda “töz” ile “ikincil nitelikler” bilimin konusu içinde yer almazlar. İkincil özellikler sübjektif olduğundan nesnel gerçeklikleri yoktur; onlar yalnızca adlardan ibarettirler. Hıristiyan bir düşünür olan Galileo yepyeni bir “ilinekler” teorisi geliştirmiş ve bunu Kilise’ye kabul ettirebileceğini düşünmüştür. Ne var ki Galileo’nun felsefi rakipleri bu fırsatı kaçırmazlar. Fırsatı değerlendiren Cizvit rahip Grassi Ratio Ponderum’da ökaristik dogmadan yola çıkarak Galileo’ya şu soruyla saldırır: “Ama bu durumda saf adları korumak için daimi bir mucizeye ihtiyaç olur mu?” (Minois, 2010: 94).

Galileo’nun eserlerinde atom teorisinin sınırlı ya da zayıf bir yer tuttuğu açıktır (Minois, 2010: 91). Başkaları onun adına yapmış olsa da, Galileo atomcu yaklaşımının ökaristik sonuçlarını hesaba katmamıştır. Bu durum, Galileo’nun bilim-dışı konulardaki spekülasyonlara genel ilgisizliğiyle açıklanabilir. Nitekim Galileo’nun atomcu felsefesi mevcut bilimsel sorunlara bir çözüm olarak ortaya çıkmıştır. Rönesans’ta Campanella ve Vives gibi çağdaşı olan düşünürlerin epistemolojilerinde yeniden canlandırılan eski atomcu görüşleri benimseyen Galileo, “maddenin ‘son derece küçük bölünmez atomlara’ ayrıştığını varsaydı. Bu varsayımıyla katının sıvı ve gaz haline dönüşmesini açıkladı. Ayrıca, birleşme, genleşme, sıkışma sorunlarını, maddenin içine-işlenebilirliğini ya da katı cisimlerdeki boş uzayları varsaymadan çözebildi.” (Burtt, 1980: 86)

Akıl mı iman mı?
Ortaçağlarda akıl ile iman arasındaki çelişki teolojinin (ilahiyatın) üstünlüğünün kabul edilmesiyle çözülmekteydi. Standart bir Ortaçağ felsefe kitabının başındaki şu sözler bu kuralı iyi özetler: “Bizim felsefemiz Hıristiyan olmalıdır ve tanrısal teolojinin hizmetkârı olmalıdır. Metafizik ilkeler teolojik hakikatleri doğrulayacak şekilde aktarılmalı ve uyarlanmalıdır.” (Minois, 2010: 45) Dinsel açıdan bakıldığında Hıristiyanlaştırılmış bir Aristotelesçilik kabul edilebilir tek felsefe olarak görülmekteydi. Bu koşullarda ileri sürülen her yeni fizik ya da astronomi sistemi, karşısında bir blok olarak din adamlarını ve Aristotelesçi filozofları bulmaktaydı.

Galileo’nun yargılanmasına neden olan -gizli ya da açık- suçlamalar ne olursa olsun sonuç ortadadır: Galileo astronomi ve fizikte yeni ve devrimci fikirler geliştirmiştir. Büyük bir iyimserlikle bilimsel teorilerini dinsel otoritelere kabul ettirebileceğine inanan Galileo’nun rakipleri saray çevresiyle sınırlı değildi. Galileo’yu felsefi alanda yenemeyen Cizvitler, ona din alanında saldırmaya karar verdiler: “Çok geçmeden Galileo’ya karşı çıkan filozoflar din bilimcilerden yardım isteyecekti. Galileo’nun fikirlerini çürütemiyorlarsa da, onu Kitab-ı Mukaddes’e ters düşmekle suçlayabilirlerdi.” (MacLachan, 2008: 62) 1614 yılının Aralık ayında Cizvitler Galileo’nun ve onun Copernicusçu görüşlerinin aleyhinde vaaz verecek bir rahip buldular. Dominiken bir rahip olan Tommaso Caccini Yeşu’nun Kitabı’ndaki bilinen ifadeleri tekrarladı. Caccini vaazının sonunda Galileo’yu, takipçilerini ve diğer matematikçileri, “şeytanın sanatını icra eden … gerçek dinin düşmanları” (Sobel, 2000: 67) olmakla suçladı. Başka bir Dominiken rahip Niccolò Lorini de Galileo’nun Benedetto Castelli’ye yazdığı ve elden ele dolaşan mektubunun bir örneğini Roma’daki Engizisyon’a ulaştırdı.

Dominiken Caccini’nin suçlamaları engizisyon tarafından araştırılmış ve bu suçlamaların asılsız olduğu kanaatine ulaşılmış olsa da Galileo artık Kilise’nin gözünde şüpheli biri olmuştu. Ancak bu sırada kendisine bir kumpas kurulduğunu düşünen Galileo’yu cesaretlendiren bir gelişme de yaşandı. 1615 Mart’ında rahip Paolo Antonio Foscarini “Copernicus sisteminin Kitab-ı Mukaddes’e aykırı olduğunun düşünülmemesi gerektiğini ileri süren” (MacLachan, 2008: 87) bir kitapçık yayınladı. Kardinal Roberto Bellarmino, Foscarini’ye 12 Nisan 1615 tarihinde bir mektup yazdı ve bu mektubun bir kopyasını Galileo’ya iletti. Bu mektubunda Bellarmino, Copernicus sistemini sadece bir çalışma hipotezi olarak aldıkları sürece güvencede olduklarını bildiriyordu:

“Yer’in gerçekten hareket ettiğini iddia etmenin tehlikeli olacağını, çünkü bunun Kitab-ı Mukaddes’le çeliştiği için Hıristiyanlığa zarar vereceğini de ilave etti. Bellarmino, Yer’in hareket ettiği kanıtlanırsa, Kilise’nin bunun asılsız olduğunu söylemek yerine, Kitab-ı Mukaddes’teki buna ters görünen bölümlerin yanlış anlaşıldığını söyleyeceğini ifade etti. Mektubunu, Yer’in hareket ettiğine ilişkin herhangi bir kanıttan haberi olmadığını belirterek bitirdi.” (MacLachan, 2008: 88)

Bellarmino’nun bu görüşüne karşılık olarak Galileo, daha önce Castelli’ye yazdığı metni geliştirerek Grandüşes Cristine’ye Mektup’a (1636) dönüştürdü. 1615 yılının sonunda Kilise’nin kendisiyle ilgili tutumunu öğrenmek için gittiği Roma’daki yetkili kişilerin eskiye oranla daha mesafeli davrandıklarını gördü. Bu sırada Engizisyon birçok teologa, Caccini’nin verdiği ifadede yer alan Copernicusçu savlarla ilgili görüşlerini sormuştu. Teologların ezici çoğunluğu bu tezlerin Kitab-ı Mukaddes’le açıkça çeliştiği ve dini inançlara aykırı olduğu yorumunda birleşmişti. Ancak bu bir rapordu ve henüz Katolik Kilisesi’nin resmi görüşü değildi.

Copernicus Devrimi
1616 yılında Katolik Kilisesi güneş-merkezli görüşleri öğreten tüm eserleri Index Librorum Prohibitorum’a (Yasak Kitaplar Listesi; kısaca, Index.) dâhil ederek okunmasını yasakladı. Copernicus’un ünlü Göksel Kürelerin Devinimleri Üzerine adlı kitabı da, üzerinde kilise yetkililerinin uygun gördüğü değişiklikler yapılana kadar bu kapsamdaydı. Böylelikle Copernicus’un yapıtı 73 yıl serbestçe okunduktan sonra yasaklanmış oluyordu. Aslında eser ilk kez yayınlandığında Kilise çevresinde de “faydalı bir el kitabı” olarak görülmüştür. Bu yapıt önceleri Roma Kilisesi tarafından olumlu karşılanmış ve Cizvit gökbilimcileri tarafından da benimsenmiştir (Trusted, 1994: 33). Copernicus sisteminin fiziksel bir gerçeği ifade ettiğinin Galileo gibi düşünürler tarafından güçlü bir şekilde savunulmasıyla birlikte yasaklar da başlamıştır. Copernicus, kendi adıyla anılan devrimin aktivisti değil teorisyeniydi. Copernicus devrimci bir ilke ortaya atmış ama bu ilkenin üstü hemen örtülmüştü. Copernicus sistemi, yıllarca, fiziksel bir gerçeklik olarak değil yalnızca faydalı matematiksel ya da gökbilimsel bir varsayım olarak kabul gördü. Galileo ise örtüyü kaldırıp mücadeleye girişti. Ancak devrim süreci karşı devrimi tetikledi ve Kilise, Yer’in gerçekten döndüğünü ileri süren kitapların basımını 1822 yılına kadar durdurdu.

Papa’nın emriyle Galileo Index’te yer alan Copernicusçu görüşlerin “kutsal metinlerle çeliştiği için savunulamayacağına ve inanılamayacağına” ilişkin karardan haberdar edildi. Bu karamsar tablo içinde umut verici gelişme, yedi yıl sonra, 1623 yılının Ağustos ayında Galileo’nun arkadaşı Kardinal Maffeo Barberini’nin Papa VIII. Urbanus olmasıyla yaşandı. O sırada yayıma hazırlamakta olduğu Il Saggiatore’yi Papa’ya ithaf etti ve 1624 baharında saygılarını sunmak üzere Papa’yı ziyaret etti. 1616 yılında Copernicus’la ilgili yasağa karşı çıkmış olan VIII. Urbanus, bu kez yasağı kaldırmayacağını söyledi. Aslında VIII. Urbanus, bilime ilgi duysa da, bilimi ortadan kaldıran şu akıl yürütmesiyle ünlüydü: “Tanrı her şeye kadir olduğundan, bütün hesaplar tersini gösterirken bile Dünya’nın gerçekten hareketsiz kalmasını sağlayamaz mı?” (Minois, 2010: 85) Papa yine de Galileo’ya, Copernicus ve Ptolemaios sistemlerini taraf tutmadan karşılaştıran bir kitap yazma izni verecek kadar sıcak davranmıştı:

“Papa, Galileo’dan saraylıları heyecanlandıracak bir kitap daha yazmasını bekliyordu. Fakat bu kitapta hiçbir koşulda Yer’in hareketinin gerçek olduğuna değinilmemeliydi. Urbanus Galileo’nun gelgit kuramından haberdardı. Bunu hoş bir hayal olarak görüyordu. Ancak Galileo, Tanrı’nın istediği şekilde gelgit yaratabileceğini açıkça belirtmeliydi. Hiç kimse, zayıf insan zekâsının Tanrı’nın eylemlerini anlayabileceğini zannetmemeliydi.” (MacLachan, 2008: 93-94)

Galileo’nun yazma izni aldığı ve üzerinde sekiz yıl çalıştığı büyük eseri Dialogo, rolleri kesin sınırlarla çizilmiş üç konuşmacı üzerine kurulmuştur: Kitapta Copernicus’un ve Galileo’nun görüşlerini, yeni bilimin matematiksel zekâsını Salviati temsil ediyordu. Aristotelesçi geleneğin önyargılarından kurtulmuş, yeni olguları kavrayabilen zekâ da Sagredo’ydu. Sadece Aristoteles’in ve resmi bilimin otoritesine inanan Simplicio ise sağduyuyu temsil ediliyordu. Ancak Latince “basit” anlamına gelen Simplicio, okuyucular tarafından akılsız biri olarak algılanabilirdi. Galileo’nun “Simplicio” adını seçmesiyle ilgili bilim tarihi yazınında iki farklı yorum göze çarpar. Kimileri, onun bu isimle altıncı yüzyılda yaşamış Aristotelesçi düşünür “Simplicius”u çağrıştırmak istediğini (Whitfield, 2008: 159), kimileri de İtalyanca “bön, basit, avanak” anlamına gelen simpleton’a bilinçli bir gönderme olduğunu savunur (Minois, 2010: 100). Olayların gelişimi ve Galileo’nun kişiliği dikkate alındığında ikinci yorum daha akla yatkındır.

Dialogo’nun şifresi
Galileo Dialogo’yu 1632 yılında tamamlayarak sansür kurulunun denetiminde yayımladı. Papanın isteği doğrultusunda önsözde ve kapanışta iki ifadeye yer verdi. Önsözdeki ifade Copernicus sisteminin fiziksel bir gerçeklik değil bir varsayım olmasıyla ilgiliydi. Galileo önsözde “Sırf matematiksel varsayıma dayanarak Copernicus’un görüşünü, tüm düşünce yollarını akıllıca tarayıp aştıktan sonra üstün göstermeye çalıştım” (Galileo, 2008: xxii) diyordu. Ancak Papa’nın bu görüşü kitapta sürekli aptal ve gülünç duruma düşürülen Simplicio’nun ağzından tekrarlanıyordu (Galileo, 2008: 597). İkinci ifade Tanrı’nın gücü ve aklının sınırsızlığıyla ilgiliydi ve bu ifade de Simplicio’nun ağzından girdi: “… Bu durum karşısında müthiş bir cüret olurdu eğer biri çıkıp da Tanrısal gücü kendi özel fantezi fikriyle sınırlamaya ya da zorlamaya kalkışsaydı” (Galileo, 2008: 634). Ancak eserin başka bir yerinde Galileo, bununla açıkça çelişen bir görüşü Salviati’nin ağzından güçlü bir şekilde dile getirmişti:

“İnsanoğlu bazı şeyleri doğanın kendisi kadar algılar. Bunlar arasında saf matematik vardır yani geometri ve aritmetik. Bunlara ait önermelerden ilahi zihin sonsuz sayıdan da fazlasını bilir, çünkü o hepsini bilir; fakat insan zihni algıladığı az sayıdaki önermeleri anlamada objektif kesinlik bakımından ilahi algılamaya eştir.” (Galileo, 2008: 138)

Galileo açıkça insani aklı temsil eden matematiksel bilginin ilahi aklı temsil eden Kitab-ı Mukaddes’e denk olabileceğini söylüyordu. Hemen harekete geçen Cizvitler Yer’in hareket ettiği düşüncesini destekleyen Dialogo’nun Protestanlara destek sağladığını ileri sürdüler. Birisi Papa’nın kulağına Simplicio’nun şahsında hakarete uğradığını fısıldadı. Aldatıldığını düşünerek taraf değiştiren Papa Galileo’nun yargılanabilmesi için Engizisyon’u harekete geçirdi. Bunun üzerine Dialogo için üç teologdan rapor istendi. Üçü de Galileo’nun Copernicus’u benimseyerek savunduğu konusunda hemfikirdi. Sonunda yetmiş yaşındaki Galileo önceden hazırlanmış bir itirafnameyi diz çökerek okumak zorunda bırakıldı:

“Kutsal Katolik Kilisesi ve Papa’nın inandığı, vazettiği ve öğrettiği her şeye daima inandığıma ve inanmaya devam edeceğime yemin ederim. (…) Güneş’in evrenin merkezinde hareketsiz durduğuna ve Yer’in evrenin merkezi olmayıp hareket ettiğine inandığım için, dini inançlara karşı geldiğim şüphesiyle yargılandım. (…) Tüm samimiyetimle ve inançla, yukarıda andığım yanlışları ve sapkınlıkları nefretle lanetler, bunlardan vazgeçtiğime ant içerim. (…) Gelecekte, ne sözlü ne de yazılı olarak, hakkımda benzer bir şüphe uyandırabilecek hiçbir şey söylemeyeceğime ve beyan etmeyeceğime yemin ederim.” (MacLachan, 2008: 83-84)

16 Haziran 1633’te Engizisyon kararını açıkladı. Dialogo yayınlanmasından on altı ay sonra Index’e alındı ve Galileo da dini inançlara karşı gelmekten ikinci derecede suçlu bulundu. 1642 yılında ölene kadar da göz hapsinde tutuldu.

Galileo olayı her şeye gücü yeten totaliter dine karşı bilimin otonomisini savunmanın simgesi olmuştur. Bu olay bilimle din arasındaki özsel ya da potansiyel karşıtlığı açığa çıkarmıştır. Anlaşmazlığın alenileşmesinde kişi ve kurumlar arasında yaşanan güç çekişmesinin ve Galileo’nun kendine duyduğu aşırı güvenin payı büyüktür.

Galileo’nun felsefi konumu
Bruno ve Kepler Rönesans düşünce geleneğinin içinde değerlendirilebileceği halde, Galileo bu gelenek içinde değerlendirilemez. Çünkü Galileo’nun düşüncesinde Rönesans’ı karakterize eden özellikler yoktur. Galileo, büyücülüğe şiddetle karşı çıkmış ve fiziksel nesnelerin çeşitliliği karşısında bir sevinç duymamıştır. Galileo “gerçeği geometrik olana indirgemek” istemiştir. Yani matematiksel fiziği kurmak için evreni geometrikleştirmiş ve bu sayede Kepler’i aşabilmiştir (Koyré, 1994: 51). O Kepler’den farklı olarak sayılara ve geometrik şekillere mistik bir tutumla yaklaşmamıştır (Trusted, 1994: 51-52).

Galileo’nun matematiği kullanması yalnızca bilimsel çalışmalar üzerinde değil, felsefi görüşler üzerinde de etkili olmuştur. Bir Copernicusçu olarak fizik ve astronomiye katkıda bulunmuş olan Galileo’nun felsefeye katkısı kısmen bilimsel çalışmalara bağlı, kısmen de bilimsel çalışmalardan bağımsız olarak ele alınabilir. Galileo’nun Dialogo adlı eseri, “Ptolemaios ve Copernicus sistemlerinin karşılaştırıldığı bir astronomi ya da fizik kitabı olmaktan çok, bu sistemlerin dayandıkları iki farklı felsefe sistemini” (Koyré, 1990: 22) karşılaştıran bir metin olarak okunabilir.

Doğanın dili: Matematik ve deney
Galileo’nun teorilerinde deney ve gözleme yer vermesi yöntem konusundaki önemli başarılarından birini temsil eder. Galileo’nun yöntem açısından diğer önemli bir başarısı, bilimsel çalışmalarında matematiği kullanmış olmasıdır. Bazı bilim tarihçileri haklı olarak Galileo’nun otoriteyle ve Aristotelesçi bilim geleneğiyle çatışması üzerinde durmuşlar, gözlem ve deneyin yeni fizik biliminin kuruluşundaki rolüne dikkat çekmişlerdir. Gerçekten de Galileo, yazılarında sık sık gözlem ve deneyin tanıklığına başvurmuştur. Ancak bu durum, yeni doğa biliminin kuruluşunda gözlem ve deneyin merkezi bir rol oynadığı anlamına gelmez. “Ortaçağ felsefecilerinin deneyi ihmal ettikleri sıklıkla söylenir ama onların deney anlayışının bizimkinden temelden farklı olduğunu söylemek daha doğru olacaktır.” (Whitfield, 2008: 106-107) Hatta gözlem ve sağduyunun kendiliğinden deneyi anlamındaki deneyin modern bilimin kurulmasında olumsuz ve engelleyici bir işlevi olduğu ileri sürülebilir. Galileo’nun sözünü ettiği deney, doğayı yöntemli olarak sorgulayan deneydir. Max Planck’ın dediği gibi “bir deney, bilimin doğaya sorduğu bir sorudur, bir ölçüm ise, doğanın soruya verdiği cevaptır”. Bu sorgulama bir dili ve sözlüğü gerektirir. Bu dil matematiksel, daha doğrusu geometrik bir dildir. Galileo’nun Il Saggiatore’deki (1623) ünlü deyişiyle:

“Felsefe gözümüzün önünde sürekli açık duran o büyük kitapta, yani evrende yazılıdır. Ancak bu kitap, kullanılan dilin anlaşılması ve yazıldığı karakterlerin bilinmesinden önce anlaşılamaz. Bu kitap matematik dilinde yazılmıştır ve onun karakterleri üçgenler, daireler ve diğer geometrik şekillerdir. Bunlar olmadan insanlık onun tek kelimesini anlayamaz ve kişi karanlık bir labirentin içinde boşuna dolanıp durur.” (Galileo, 2008b: 183)

Görüldüğü gibi Galileo, “matematik” ile “doğa” arasında bir uygunluk olduğu görüşünü açık bir şekilde dile getirmektedir. Doğada kimsenin ve Aristotelesçilerin göremediği daireler, üçgenler, küreler, doğrular görmektedir. Daha doğrusu buna kalkışmaktadır. Bugün bizler de böyle şeyleri görmediğimiz halde, tıpkı Galileo gibi yine de var olduklarına inanıyoruz. Bu görüşün bir sonucu, ancak matematiksel bir yöntem kullanan doğa felsefesinin (yani fiziğin) doğru bilgiye ulaşabileceğidir. Peki, Galileo bu doğa görüşüne nasıl ulaştı?

Galileo, dönemin yaygın yaklaşımını dile getiren hocası Francesco Bounamici ve meslektaşı Jacobi Mazzoni’den, bilimde matematiğin rolüne ilişkin Aristoteles ile Platon arasında “temel bir çatışma” olduğunu öğrendi. Bu dönemdeki Platoncular matematiğe üstün bir yer vererek, fizikte kullanılabileceğini savunmuşlardır. Aristotelesçiler ise matematiği soyut bir bilim olarak görmüş, matematiğe -fizik gibi gerçek varlığı inceleyen bilimlerden- daha az değer vermişlerdir. Aristoteles için sağlıklı kişilerin doğal koşullar içindeki algı ya da duyuları “bilginin güvenilir rehberi”ydi (Musgrave, 2013: 55). Dolayısıyla Aristotelesçilere göre fizik deneye ve algıya dayanıyordu ve matematiğin rolü ikinci derecedendi (Koyré, 1994: 125-126). Bununla birlikte “matematik kanıtların kesinliği” konusunda Platoncular ve Aristotelesçiler uzlaşmışlardı. Asıl sorun, matematik kanıtların gerçekliğe denk düşüp düşmeyecekleri ve matematiğin bilimin yapısı içindeki rolü, başka bir deyişle de bizzat gerçekliğin ne olduğu sorunu olmuştur. Örneğin “bir çemberin yanından geçen ve ona ancak bir noktada değen doğru olan” teğete ya da “çember çevresinin uzunluğunun çapının uzunluğuna bölünmesi ile elde edilen sabit sayı” olan pi sayısını Yer’in üzerinde (gerçeklikte) kimse göremez. Aristotelesçiler de böyle bir şey görmediklerinden buna inanmayı haklı olarak reddetmişlerdir.

Koyré’ye göre bu dönemde iki ayrı Platoncu gelenek vardır. Bunlardan biri sayılar üzerine mistik kurgular yapan gelenek, diğeri matematiksel bilim geleneğidir. Galileo, matematiksel bilim geleneğini temsil eden Platoncu akım içinde yer alır (Koyré, 1994: 138,154). Bu saflaşmada Galileo felsefi konumunu açıkça belirtir:

“Pythagorasçıların sayıların bilimine çok büyük saygı duyduklarını, Platon’un kendisinin insan zekâsına hayran olduğunu, insanın, sırf sayıların yapısını anlayabildiği için, tanrısal olandan pay aldığına inandığını pek iyi biliyorum. Ben kendim de bu yargıyı taşımaya eğilimliyim.” (Koyré, 1994: 129)

Ancak Galileo’nun Platonculuğu dönemin Platonculuğundan farklıdır. Matematiğin bilimlerdeki rolü konusunda yürütülen tartışmalarda “hem Platoncuların hem de Aristotelesçilerin üzerinde uzlaştıkları öncülü, yani matematiksel kavramların soyut karakterini, kusursuz figürlerin ontolojik ayrıcalıklarını” reddetmiştir. Galileo, matematik kavramların ya da geometrik şekillerin maddede her zaman somut bir halde var olduğunu söylemiştir. Bu durumda geometrik bir şekil fiziksel bir gerçekliğe sahip olmakla ideal karakterinden örneğin ‘küreliğinden’ bir şey kaybetmez. Bir cismin küre olup olmadığına o cismin gerçek olup olmadığına bakılarak değil, küre tanımına uyup uymadığına bakılarak karar verilir. Galileo’nun bu orijinal görüşünün, “geometrik formların maddeden ayrı olmaması”nın doğrudan bir sonucu, geometrik yasaların fizikte de geçerli olmasıdır. İşte doğa bu nedenle matematiksel bir dille konuşmaktadır. Bu dilin karakterleri üçgenler, çemberler ve doğrulardır. Bu nedenle doğayı matematiğin diliyle sorguya çekmek gerekir (Koyré, 1990: 23-24).

Galileo, Platoncu bir görüşü (“bilmek anlamaktır”) olduğu gibi yinelemiştir: “Ben size diyorum ki, bir insan hakikati kendiliğinden bilmiyorsa, herhangi birinin ona bu bilgiyi vermesi olanaksızdır.” (Koyré, 1994: 130) Fakat Galileo, eserlerinde Platon’a olumlu göndermeler yapmış, Sokratesçi düşündürme (doğurtma) yöntemini kullanmış olsa da, Galileo’nun Platonculuğu, “evrenin matematiksel bir işleyişi, matematiksel bir karakteri olduğu düşüncesinin” ilerisine geçmemiştir (Koyré, 1990: 24).

Koyré’ye göre Galileo, “bilmek anlamaktır” görüşünü fiziğe de uygulamıştır: “İyi fizik a priori yapılır. Kuram olgudan önce gelir. Deney gereksizdir; çünkü her deneyden önce, aradığımız bilgi elimizdedir zaten.” (Koyré, 1994: 153) Salviati’nin ağzından “Ben hiç deney yapmadan, sonucun söylediğim gibi çıkacağından eminim: Çünkü böyle bir sonuç vermesi gerekiyor” demiştir (Galileo, 2008a: 199-200). Burtt’ün işaret ettiği gibi Galileo’nun bu “matematiksel apriorizmi olası aşırılıklar” içerir ve Galileo “bu aşırılıkları ciddi olarak göz önünde bulundurmamıştır”. Ancak diğer yandan Galileo için bilgimizin nesnesi “duyusal dünyadaki” nesnelerdir; “duyusal olgular açıklanmak için önümüzde durmaktadır, görmezlikten gelinemezler” (Burtt, 1980: 77). Galileo, matematik kadar deneyi de vurgulamayı ihmal etmemiştir. Ancak Galileo’nun yeni bilimi nasıl yeni bir deney türünü zorunlu kaldıysa, aynı şekilde yeni bilimin ihtiyaçlarını karşılayacak yeni bir matematiğin geliştirilmesine de yol açmıştır:

“Klasik matematik, niceliklerin hesaplanmasında kullanılan aritmetikten ve alan hesaplamalarında kullanılan geometriden ibaretti. İki alan da statik unsurlarla ilgilenmekteydi. On yedinci yüzyıl bilim adamları fizik kuvvetlerin dünyasını keşfetmeye başlayınca, zaman konum, güç ve hız gibi dinamik unsurların hesaplanmasına elverecek yeni bir matematiğe gereksinim duyulur oldu. Matematiğin değişimi ve hareketi analiz edebilmesi için önce dilinin daha güçlü ve esnek hale gelmesi gerekiyordu.” (Whitfield, 2008: 186)

Yukarıda işaret edildiği gibi doğa kendisini “duyu dünyası” aracılığıyla değil, yalnızca matematiksel bir dil aracılığıyla ifade edebilmektedir. Öyleyse, bu durumda “duyu dünyası” da doğanın doğaya yabancı bir dil aracılığıyla ifade edilmesinden başka bir şey değildir. Galileo’ya göre, uzun süre yanlış yoldan gittikten sonra insanlık, doğanın dilinin matematik olduğunu keşfetmiştir. Galileo’nun bu görüşünü “bilimsel olarak bilinebilir olan, ölçülebilir olandır” biçiminde özetlemek mümkündür.

İkincil niteliklerin öznelliği
Nitel bilgi yerine matematiksel bilginin ön plana çıkması birincil ve ikincil nitelikler arasında bir ayrım yapılması demektir. Galileo için birincil nitelikler objektif, ikincil nitelikler sübjektiftir; birincil nitelikler, “nesnelerin sayı, şekil, hareket, durum, genişlik olarak bilinen yönleri”; ikincil nitelikleri ise “renk, ses, koku gibi duyu organlarımıza bağlı olarak elde” edilen özelliklerdir:

“Matematiksel metafiziğin doğasında varolan zorunluluklar Kepler gibi Galileo’yu da birincil ve ikincil nitelikler öğretisine götürdü… Galileo’nun yaptığı açık ayrıma göre birincil nitelikler mutlak, nesnel, değişmez ve matematiksel; ikincil nitelikler ise göreli, öznel, değişken ve duyulur özellikteydi. Birincil nitelikler ilahi ve insani bilgi dünyasıdır; ikincil nitelikler görüş ve yanılsama dünyasıdır.” (Burtt, 1980: 83)

Kepler için olduğu gibi Galileo için de nesne hakkında bilimsel bilginin kaynağı sayı, şekil, büyüklük, yer ve hareket gibi matematiksel olarak ifade edilebilen birincil niteliklerdir. Evren temelde geometrik bir yapıdadır. Diğer özellikler birincil niteliklerin sonucuna bağlı olarak ortaya çıkan ikincil niteliklerdir. Galileo’nun asıl önemli iddiası ikincil niteliklerin öznel olduğu görüşüdür (Burtt, 1980: 84). Galileo II Saggiatore adlı yapıtında fiziksel nesnelerin ikincil niteliklerinin sübjektif olduğu, yani yalnızca algılayan kişinin zihninde var olduğu görüşünü ifade etmiştir:

“Şimdi, diyorum ki, her ne zaman maddi ya da cisimsel bir tözü tasavvur etsem, hemen onu sınırlı olarak ve şu ya da bu şekle sahip olarak, diğer şeylere kıyasla büyük ya da küçük olarak ve herhangi bir verili zamanda belirli bir yerde, devinim veya dinginlik halinde, başka bir cisme değiyor ya da değmiyor olarak, sayıca tek, az ya da çok olarak düşünme ihtiyacı hissediyorum. İmgelemimi ne kadar zorlasam da böyle bir tözü bu koşullardan ayıramıyorum. Fakat beyaz ya da kırmızı, acı ya da tatlı, gürültülü ya da sessiz ve hoş ya da pis kokulu olması gerektiğini ise, zihnim zorunlu eşlikçiler olarak devreye sokmak gereğini hissetmiyor. Rehberimiz olarak duyular olmaksızın, yardımsız akıl ya da imgelem muhtemelen bu gibi niteliklere asla ulaşamazdı. Bu yüzden, tatların, kokuların, renklerin vb… yalnızca bilincin içinde bulunduklarını düşünüyorum. Bu yüzden, şayet canlı varlıklar ortadan kaldırılacak olsa, bütün bu niteliklerin de silineceğini ve yok olacağını düşünüyorum.

“Bizde tat, koku ve ses duyumları uyandırmaları için, dış cisimlerde şekillerden, sayılardan ve yavaş ya da hızlı devinimlerden başka bir şey olması gerekmediği kanısındayım. Sanırım eğer kulaklar, diller ve burunlar ortadan kalksa, şekiller, sayılar ve devinim kalır, ama kokular, tatlar ya da sesler kalmazdı.” (Musgrave, 2013: 146)

Görüldüğü gibi Galileo, çok açık bir şekilde fiziksel nesnelerin birincil nitelikleri olan sayı, şekil, hareket, durum gibi özelliklerinin insanların bilincinden ve duyularından bağımsız var olduğunu ya da insan türü yeryüzünden yok olsa bile var olmaya devam edeceğini ifade etmektedir. Bunun tersine ikincil nitelikler olan koku, tat ve ses gibi özelliklerin insanın duyu organlarının varlığına bağlı olduğunu ileri sürmektedir.

Burtt’ün işaret ettiği gibi, Galileo’nun birincil ve ikincil nitelikleri tanımlama biçimi, daha doğrusu ikincil niteliklerin sübjektifliği görüşü “modern düşünceyi etkilemesi bakımından” oldukça önemlidir. Çünkü Galileo’nun söz konusu nitelikleri tanımlama biçimi ile “insanı ve doğayı tamamen ayırmış” ve epistemolojik anlamda insanı önemsiz kılmıştır. Galileo’ya göre “gerçek dünya” insanın dışındadır (Burtt, 1980: 89). Bu nedenle doğanın ya da fiziksel nesnelerin yapısının insanın anlama yeteneğine olan önceliği vardır:

“Doğa, önce insanların beyinlerini oluşturup sonra insanların anlama kapasitelerine göre şeyleri inşa etmez; tersine, önce nesneleri kendi biçimine göre yapar ve sonra büyük emekler pahasına da olsa kendi gizlerinden birkaçını ortaya çıkarabilecek olan insanın anlama yetisini inşa eder.” (Burtt, 1980: 78)

Diğer bir deyişle doğa, insanın düşünce ve yargılarından etkilenmez. Galileo’ya göre doğa insan tarafından değiştirilemez ve “asla çiğnenemez sabit kanunlara” göre işler (Burtt, 1980: 75). Galileo’nun metafiziğine göre, “insan ile gerçek dünya arasındaki tek ortak nokta insanın gerçeği keşfedebilme yeteneğidir. Bir yanda insan, diğer yanda insanın dışında yer alan gerçek dünya. Tam bir Kartezyen düalizmi.” Galileo’nun “insan” ile “doğa” arasında kabul etmiş olduğu bu ilişki biçimi, düşünce tarihinde insanın “ilk kez pasif ve önemsiz bir varlık olarak” ele alınması anlamına gelir. Diğer bir deyişle Galileo’nun sisteminde insan, doğa karşısında “konu dışı bir izleyici, gerçekliğin tözü olan büyük matematiksel sistemin önemsiz bir sonucu” olarak kabul edilir (Burtt, 1980: 90). Albert Camus’nün Sisifos Efsanesi’nde söylediği gibi:

“Dünyanın ‘yoğun’ olduğunu ayrımsamak, bir taşın ne denli yabancı, bizce kavranılmaz olduğunu, doğanın, bir görünümün bizi ne büyük bir güçle yok sayabileceğini sezinlemek. Her güzelliğin dibinde insan dışı bir şey yatar ve bu tepeler, gökyüzünün bu tatlılığı, bu ağaç dizileri kendilerine yüklediğimiz düşsel anlamı hemen o dakikada yitiriverir, yitirilmiş bir cennet kadar uzaktırlar bundan böyle. Binyıllar ötesinden dünyanın ilkel düşmanlığı yükselir bize doğru. Yüzyıllar boyunca onda yalnızca kendisine önceden verdiğimiz biçimleri ve çizgileri anlamış olduğumuza göre, bundan böyle bu yapmacıklığı sürdürmeye gücümüz yetmediğine göre, bir saniye için onu anlamaz oluruz. Yeniden kendi kendisi olduğuna göre, dünya bizce anlaşılmaz olur.” (Camus, 2011: 32)

 Galileo ve basitlik ilkesi
Galileo, Copernicusçu dünya görüşünü savunmak, serbest düşme hareketi yapan cisimlerin hareketini açıklamak ya da metafizik nedenlerle “basitlik ilkesi” kullanmıştır. Galileo için “basitlik”, her durumda uyulması gereken bir ilkedir: “Aristoteles’in son derece doğru özdeyişi bize, bir tek yoldan elde edilmesi mümkün şeyi birçok yoldan elde etmeye çalışmanın gereksizliğini öğretir.” (Galileo, 2008a: 169) Böylece Galileo, Aristoteles’ten beri geçerliliğini koruyan bu kavramı açıkça kullanır.

Galileo Copernicus sistemini savunurken basitlik ilkesinden faydalanmış ve Ptolemaios ve Tycho Brahe’nin sistemlerini “karmaşık” olarak nitelemiştir. Basitlik ilkesi Galileo’nun eylemsizlik ilkesine ulaşmasında da rol oynamıştır:

“Hiçbir değişiklik meydana gelmediğinde bir şeyin olduğu halde kalması ona çok basit görünür. Kepler bir şeyin kendiliğinden, dururken hareket edemeyeceği önermesini benimsiyordu. Galileo ise daha ileri giderek bir şeyin kendi kendine ne hareket edebileceğini ne de hareket ederken durabileceğini keşfetti. Bu yasaya daha sonra -Kepler’in bir deyimine karşılık olarak- eylemsizlik ilkesi dendi.” (Höffding, 1955: 180)

Gerçekten de Galileo kendi hareket, uzay ve eylemsizlik gibi temel kavramlarını deney ve gözlemden çıkarmamıştır. Galileo için hareket göreli, sürekli ve tözsel bir durumdur (Koyré, 1994: 143). Galileo, Aristoteles fiziğinin tersine, hareketi bir değişim süreci olarak değil, bir durum olarak kavrayabildiği için eylemsizlik ilkesine ulaşabilmiştir. Eylemsizlik ilkesine uygun hareket (yani düzgün doğrusal hareket) yapan bir cisim normal koşullarda gözlenemeyeceği için söz konusu ilkeye kavramsal yoldan ulaşılmış olması şaşırtıcı değildir. Aslında Galileo, söz konusu ilkeye “düşünce deneyiyle” ulaşır. (Galileo’nun tasarladığı düşünce deneyi için ayrıca T. S. Kuhn’a (1994: 297-318) bakılabilir.) Keşif yolunun kanıtlama yolundan farklı olduğunu ifade etmiş olan Galileo, metafizik yoldan ulaştığı sonuçları ayrıca deneylerle kanıtlamıştır (Höffding, 1955: 180). Galileo, Descartes’ın tersine, -Descartes’ın evreni o kadar karmaşıktır ki, belirli bir fenomenin tek başına ele alınabilmesi mümkün değildir- bilimsel çalışmalarında her zaman basitliğin sağladığı olanakları kullanmıştır:

“Galileo’ya göre evrenin en temel özelliklerinden birisi de, işleyişindeki basitliktir. Bu basitlik, evrenin genel yasalarına basit fenomenlerin incelenmesi yoluyla ulaşılabilmesini sağladığı gibi, elde edilen yasaların doğaya uygunluklarının deney yoluyla araştırılmasına da olanak verir.” (Koyré, 1990: 24)

Höffding’e göre “Copernicus ve Bruno zamanında dünyanın yeni kavrayış biçiminin yeni bir bilgi sorununa yol açacağı” belli olmuş ve Galileo ise bu sorunu “çok daha güçlü bir şekilde ortaya” koymuştur. Bu nedenle Galileo, “pek çok önemli soruda basitlik ilkesini” temel alır. Galileo’ya göre doğanın basitliği ile bu basitliğe inanmamızı sağlayan nedenleri birbirinden ayırt etmemiz gerekir:

“Bizim anlamakta güçlük çektiğimiz şeyleri doğa kolaylıkla gerçekleştirir. Burada varoluş ve bilgi arasında kararlı bir karşıtlık ortaya çıkar. Galileo bu karşıtlığın matematiksel bilgi gibi sahip olduğumuz en açık bilgide belli bir derecede ortadan kalktığı görüşündedir. Burada insan bilgisi, Tanrı’nın varoluşla ilgili gerçekleri bildiği görüşüne yönelir. Bizim birçok sonuçlardan sonra ulaştığımız yere Tanrı basit bir sezgiyle varır. Bu noktada basitlik ve karmaşıklık arasındaki karşıtlık halen devam etmektedir.” (Höffding, 1955: 182)

Evrenin bitimsizliği
Ptolemaios, Copernicus ve Kepler’den farklı olarak Galileo, evrenin “sabit yıldızlar küresi tarafından sınırlandığını kabul” etmemiştir. Galileo, sonsuz evren düşüncesine eğilim duymasına karşın bu sorunu çözmeye çalışmamıştır. Galileo “evrenin sonluluğu ya da sonsuzluğu tartışmasında” taraf tutmamıştır (Koyré, 1998: 76, 78). Ancak Koyré’ye göre Galileo bu konudaki görüşünü açıkça söylememiş olsa da, Galileo’nun evreninin “göksel bir kubbeyle sınırlı” bir evren olduğu söylenemez (Koyré, 1994: 51). Höffding de aynı kanıdadır: “Galileo, hemen hemen, Bruno ile birlikte uzayın sonsuzluğunu varsaymaya başlamıştır. Dünyanın merkezi noktasının doğruluğu konusunda şüpheleri vardır. Bu konudaki kesin görüşünü bildirmemesinde Bruno’nun başına gelenler etkilidir.” (Höffding, 1955: 179)

Koyré’nin işaret ettiği gibi Galileo, evrenin bir merkezi olduğu görüşünü reddetmiştir. Galileo’nun deyişiyle “evrenin nerede bulacağımızı ya da varolup olmadığını bile bilemediğimiz merkezi” yoktur. Galileo’nun bu düşüncesi Ptolemaios, Copernicus ve Kepler’in bir merkez (Dünya ya da Güneş) varsayan evren görüşünden farklıdır. Galileo’nun yaklaşımı Cusalı Nicholas ve Giordano Bruno’nun merkezsiz kozmolojileri ile uyum içindedir (Koyré, 1998: 79).

Galileo, “fırlatılan cisimleri ne hareket ettirir?” sorunu üzerinde yoğunlaşmış ama “gezegenleri ne hareket ettirir?” sorunu üzerinde durmamıştır. Galileo, bu nedenle, evrenin sonsuzluğu gibi bir sonuca da ulaşamamıştır. Fakat Galileo fiziğinin bazı özellikleri evren anlayışının sonlu olmadığına işaret etmektedir. Galileo, Liceti’ye yazdığı bir mektubunda evreni “bitimsiz” (“interminate”) olarak nitelemiştir. Bu terimin, Galileo’dan önce Cusalı Nicholas tarafından kullanıldığı bilinmektedir (Koyré, 1998: 81).

Kavramların yeniden tanımlanması
Aristoteles’e bilinçli olarak karşı çıkmış olmasına ve fiziğindeki birçok kavramı eleştirmiş olmasına karşın Galileo, birçok düşünür gibi yine de ondan etkilenmiş ve bazı kavramlarını kullanmaya devam etmiştir. Örneğin Aristoteles’in hareket tanımında saklı olan animizmden etkilenen Galileo dairesel hareketin doğrusal hareketten daha mükemmel olduğu inancını da paylaşmıştır (Trusted, 1994: 49). Ancak birincil ve ikincil nitelikler arasındaki ayrım ve bu ayrımın arka planında yatan anlayış, Ortaçağ’dan beri, Aristotelesçi bir içerikle kullanılagelen felsefi kavramların yeni bir anlayışla aşama aşama tanımlanması anlamına gelmektedir. Daha önce de işaret edildiği gibi Ortaçağ’ın fiziksel nesne anlayışına göre fiziksel nesnelerin içinde bir erek vardır ve bu erek bir forma yönelir. Diğer bir deyişle fiziksel nesneler teleolojik bir yaklaşımla ele alınmış ve bunların on kategorik özelliği olduğu varsayılmıştır. Bu yaklaşıma göre ilk dokuz kategori fiziksel nesnelerin görünen özellikleriyle ilgilidir. Onuncu kategorinin ise, bu nesnelerin değişmeyen asıl özelliğini yani tözünü oluşturduğu kabul edilir:

“Bu görüşün mantıksal sonucu, asıl varlığın görünebilir olmadığı, ancak idrak edilebilir olduğudur. Duyumlar yalnızca form’u bildirebilir. Bu form, bir fiziksel varlığın daha önce içine konulmuş bir erek’e ulaşmak için aldığı biçimdir, görünüştür. Diğer bir deyişle, potansiyel olanın aktüel hale gelmesidir. Mevcut durum yani aktüel olan, fizik varlık aracılığıyla formun kendisini ifade etmesidir.” (Ural, 1994: 37)

Aristotelesçi anlayışta fiziksel nesnelerdeki değişim, söz konusu nesnenin bir ereğe ulaşma eğilimi olarak görülmüştür. Teleolojik anlayışta bütün nesnelerin (evrenin) bir ereği mevcuttur: “Bu görüş organik bir evren anlayışını da beraberinde getirmektedir. Çünkü evren, fizik varlıkların organik bir bütünlüğü olarak tasarlanmaktadır. Bu bütünlük içinde her eleman kendine has ve diğerinden farklı özelliklere sahiptir.” (Ural, 1994: 37) Bir organizmadaki organların belli bir yeri ve fonksiyonu olması gibi bu evren kavrayışında da bütün maddelerin belli bir yeri ve fonksiyonu vardır.

Modern bilimin kuruluşunun gecikmesinin nedenlerinden biri bizzat Aristoteles fiziğinin yapısıdır. Aristoteles fiziği oldukça gelişmiş ve tümüyle tutarlı bir bilimsel teoridir. Ayrıca bu fizik, derin bir felsefi temele dayanır ve modern bilime kıyasla, sağduyu ve günlük tecrübeyle çok daha iyi uyuşur. Galileo ise, deney ve duyu algısını değil, salt, katışıksız düşünceyi temel alır ve yeni bilim anlayışını bu sayede geliştirir. Galileo’nun yaklaşımına göre, sağduyu, nesneleri düşünmemize değil nesneleri tasarlamamıza yardımcı olabilir. Koyré’nin deyişiyle (1994: 143) “sağduyu Ortaçağlı ve Aristotelesçidir, hep de öyle olmuştur.”

Copernicus’la başlayan ve Galileo ile devam eden yeni evren anlayışı, Aristoteles’in fizik ve metafizik sisteminin temel kavramlarında radikal değişikliklere yol açmıştır.  Bu yeni anlayışta evren, organik bir bütünlük olarak görünmekten çıkmış, hareketleri matematik bir dille açıklanabilir hale gelmiştir. Diğer bir deyişle nitel olarak bölünmüş evren anlayışından homojen ve matematiksel bir evren anlayışına geçilmiştir. Dolayısıyla nesneler arasında da nitel değil matematiksel bir fark söz konusudur.

Rönesans’la başlayıp Yeniçağ’da devam eden felsefi görüş ile Antikçağ felsefesi arasında kökten bir fark ortaya çıkar. Bu kökten değişiklik birçok temel kavramın anlamlarındaki değişikliği içermektedir. Bilim ve felsefenin kavramlarının değişiminde “hareket” gibi bazı kavramların diğerlerine göre “daha merkezi rolü” olduğu söylenebilir. Copernicus, Kepler ve Galileo’nun cisimlerin hareketini matematiksel bir yolla betimlemesi başta fiziksel nesneler olmak üzere birçok fenomenin yeni bir bakış açısından kavranmasını sağlamıştır. Nitekim Galileo, kuvvetin özünün değil neden olduğu harekete bakılarak matematiksel yolla ölçülebilen yönünün bilinebileceğini ileri sürmüştür:

“Her şeyden önce hareketin nasıl olduğunun matematiksel incelenmesi kaçınılmaz olarak uzay ve zaman kavramlarının önem kazanmasını sağlamıştır. Hareketin herhangi bir durumunu matematiksel olarak ele aldığımızda, belli zaman birimlerini kapsayan belli uzaklık birimlerini analiz ederiz. Bu, Antikçağ’da astronominin ilgi alanına girdiği kadarıyla eksik bir şekilde fark edilmiştir; herhangi bir gezegensel hareketin matematiksel yöntemlerle göklerin geometrisi içinde izini sürmek, zaman kavramının kabul edilen ölçütleri olan mevsimler, günler ve saatlerin açıkça düzenli olarak birbirini izleyen belli durumlarıyla, gök küresindeki gezegenin art arda tekrarlayan durumlarını ilişkilendirmek anlamına geliyordu. Ancak Antikçağın metafizik düşünceleri, büyük ölçüde insanın yaşamı ve ilgileri göz önüne alınarak biçimlendi ve oldukça farklı bir terminolojiye yol açtı. Hareketi, uzay ve zaman içinde matematiksel olarak analiz etme olanağının önemli sonuçları görülemedi ve zamanın doğası hakkında en temel sorular diğer bağlantılar içinde ortaya çıktı. Skolastik felsefede ve Aristoteles fiziğinde nicel yönteme karşı nitel yöntem yalnızca uzay ve zamanı önemsiz kılmadı ama Aristoteles fiziğinde en azından Platoncular ve Pythagorasçılarca ortaya konulandan kökten farklı bir tanıma yol açtı ve daha çok matematiksel yönteme uydu. Aristoteles’e göre uzay, uzamlı olduğu ölçüde bütün nesnelerin altında yatan bir şey değil, nesneler tarafından işgal edilen bir şeydir; herhangi bir nesne ile onu kuşatan şeyler arasındaki sınırdır. Nesnenin kendisi geometrik bir şeyden çok nitel bir tözdür. Aristotelesçi fiziğin bu şekildeki düşünme alışkanlığının üstesinden, yavaş yavaş, ancak yeni bilim sayesinde gelinebilirdi; insanlar nesneler ve onların ilişkilerinin temelde matematiksel olduğu düşüncesine kendilerini birden alıştıramazlardı. Ancak, Yeni-Platonculuğun yeniden yükselişi -ve dönemin matematiksel ilerlemeleri- ki bunlar Copernicus astronomisinde doruğa ulaşır bu alışkanlığa katkıda bulundu. Fiziksel uzayın geometrinin dünyasıyla özdeş olduğu ve fiziksel hareketin saf bir matematiksel kavram olma özelliği kazandığı varsayıldı. Böylece Galileo’nun metafiziğinde uzay (ya da uzaklık) ve zaman temel kategoriler oldular. Gerçek dünya, matematiksel olana indirgenebilen hareketlerdeki cisimlerin dünyasıdır ve bu, gerçek dünyanın, uzay ve zaman içinde hareket eden cisimlerin dünyası olduğu anlamına gelir. İçinde Skolastik felsefenin değişim ve hareketi analiz ettiği teleolojik kategoriler yerine artık biz daha önce değersiz bulunan mutlak matematiksel süreklilik olarak yeni anlamlar yüklenen ve en yüksek metafiziksel nosyonlar statüsüne yükseltilen bu iki kendiliğe sahibiz. Yani gerçek dünya, uzay ve zaman içinde matematiksel olarak ölçülebilen hareketlerin dünyasıdır.” (Burtt, 1980: 92-93)

Görüldüğü gibi Galileo’nun hareketi yeni bir bakışla matematiksel bir şekilde tanımlaması, aynı bakışla ve yeni hareket kavramıyla uyumlu bir şekilde uzay ve zaman kavramlarının da yeniden tanımlanmasına yol açmıştır. Kavramların zincirleme bir şekilde yeniden tanımlanması yeni bir evren tasarımının ortaya çıkması anlamına gelir. Diğer bir deyişle Copernicus, Kepler ve Galileo’nun birçok fenomenin yeni bir bakış açısından kavranmasını sağlayan kavramları, aynı zamanda yeni bir sorunsalın ortaya çıkması anlamına gelir. Söz konusu sorunsalın oluşumunda “modern felsefenin kurucusu” olarak kabul edilen Descartes’ın ayrı bir yeri vardır.

Kaynaklar

1) Akdoğan, Cemil (1996), Bilim Tarihi, Eskişehir: A.Ü.A.F. Yayınları.

2) Bixby, William (1997), Galileo ve Newton’un Evreni, çev. Nermin Arık, İstanbul: Tübitak ve Yapı Kredi Yayınları.

3) Blackwell, Richard J. (2016), “Galileo Galilei”, Batı Geleneğinde Bilim ve Din Tarihi, Gary B. Ferngren (editör), çev. Ümit Hüsrev Yolsal, İstanbul: Say Yayınları, 142—148.

4) Burtt, Edwin Arthur (1980), The Metaphysical Foundation of Modern Physical Science, London: Routledge & Kegan Paul.

5) Camus, Albert (2011), Sisifos Söyleni, çev. Tahsin Yücel, İstanbul: Can Yayınları.

6) Drake, Stillman (1989), Galileo, Oxford: Oxford University Press.

7) Feyerabend, Paul Karl (1991), Yönteme Hayır, çev. Ahmet İnam, İstanbul: Ara Yayıncılık.

8) Galileo Galilei (2011), İki Yeni Bilim Üzerine Diyaloglar, çev. Yasemin Çevik, Ankara: Elips Kitap.

9) Galileo Galilei (2009), Dante’nin Cehennemi Üzerine Dersler, çev. Murat Sirkecioğlu, İstanbul: Bilge Kültür Sanat.

10) Galileo Galilei (2008a), İki Büyük Dünya Sistemi Hakkında Diyalog, çev. Reşit Aşçıoğlu, İstanbul: Türkiye İş Bankası Kültür Yayınları.

11) Galileo Galilei (2008b), The Essential Galileo, edited and translated by Maurice A. Finocchiaro, Indianapolis: Hackett Publishing Company.

12) Grant, Edward (1986), Orta Çağda Fizik Bilimleri, çev. Aykut Göker, Ankara: V Yayınları.

13) Henry, John (2009), Bilim Devrimi ve Modern Bilimin Kökeni, çev. Selim Değirmenci, İstanbul: Küre Yayınları.

14) Höffding, Harald (1955), A History of Modern Philosophy, New York: Dover Publications, Inc.

15) Kitab-ı Mukaddes (1985), İstanbul: Kitab-ı Mukaddes Şirketi yayını.

16) Koyré, Alexandre (1998), Kapalı Dünyadan Sonsuz Evrene, çev. Aziz Yardımlı, İstanbul: İdea Yayınevi.

17) Koyré, Alexandre (1994), Yeniçağ Biliminin Doğuşu, çev. Kurtuluş Dinçer, Ankara: Gündoğan Yayınları.

18) Koyré, Alexandre (1990), “Galilei Üstüne”, çev. Ender Abadoğlu ve Aydın Akkaya, Bilim ve Mühendislik, 2: 1-32.

19) Kuhn, Thomas S. (2007), Kopernik Devrimi / Batı Düşüncesinin Gelişiminde Gezegen Astronomisi, çev. Halil Turan vd., Ankara: İmge Kitabevi Yayınları.

20) Kuhn, Thomas S. (1994) Asal Gerilim / Bilimsel Gelenek ve Değişim Üzerine Seçme İncelemeler, çev. Yakup Şahan, İstanbul: Kabalcı Yayınevi.

21) MacLachan, James (2008), Galileo Galilei, çev. İnci Kalınyazgan, Ankara: TÜBİTAK Kitapları.

22) Minois, Georges (2010), Galileo, çev. Işık Ergüden, Ankara: Dost Yayınları.

23) Musgrave, Alan (2013), Sağduyu, Bilim ve Şüphecilik – Bilgi Kuramına Tarihsel Bir Giriş, çev. Nur Küçük, İstanbul: İthaki Yayınları.

24) Sobel, Dava (2000), Galileo’nun Kızı [bilim, inanç ve sevgi üstüne tarihsel bir inceleme ], çev. Bahadır Sina Şener, İstanbul: Türkiye İş Bankası Kültür Yayınları.

25) Tez, Zeki (1995), Doğa Karşısında Pratik ve Teknik Uğraşı, Ankara: Kültür Bakanlığı Yayınları.

26) Trusted, Jennifer (1994), Physics and Metaphysics: Theories of Space and Time, London and New York: Routledge.

27) Ural, Şafak (1994), Bilim Tarihi, Cilt III, İstanbul: Ağaç Yayınları.

28) Vigoureux, Jean-Marie (2008), Newton’un Elmaları, çev. Nedim Demirbaş, İstanbul: Alkım Yayınevi.

29) Westfall, Richard S. (1995), Modern Bilimin Oluşumu, çev. İsmail Hakkı Duru, Ankara: TÜBİTAK Kitapları.

30) Whitfield, Peter (2008), Batı Biliminde Dönüm Noktaları, çev. Serdar Uslu, İstanbul: Küre Yayınları.