Bu yazıda çok bilinen bir mantık bilmecesinin iki çeşitlemesini ele alacağız. Sözünü edeceğimiz mantık bilmeceleri çok eskidir ve o kadar popüler olmuşlardır ki, çoğumuz bu sorularla ilk kez ne zaman karşılaştığımızı anımsamayız bile. Birinci bilmeceyi fazla tanıdık buluyorsanız ve hikâyesinin erkek egemen dünyanın diliyle yazılmış olmasına tepkiliyseniz diğer bilmeceye göz atmanızı öneririm. İkinci bilmece de klasik bir sorudur, ama vereceğimiz çözüm son derece sıradışı ve şık. Öte yandan bu bilmecenin hikâyesinde kadınlar erkeklerin baskı ve dayatmalarına boyun eğmeyecek, kendi kurallarını koyacaklardır.
Birinci Bilmece. Üç güzel kadın ve onların eşleri yaşadıkları sahil kasabasının karşısındaki adaya bir sandalla gitmek isterler. Sandal sadece iki kişi taşıyabilmektedir. Ayrıca kadınların kocaları çok kıskançtır, eğer eşleri başka erkeklerle bir arada olursa aldatılma korkusu yaşadıklarından kendilerinin olmadığı ve diğer erkeklerin bulunduğu bir ortamda eşlerinin kalmasını izin vermezler. Sorumuz şöyle: Bu üç çift, bu koşullarda kasabadan adaya nasıl geçerler?
Çözüm. Problemin koşullarını sıralayalım: Üç evli çift kıyı kasabasından adaya sadece iki kişi taşıyan bir sandalla gidecekler. Hem kasabada hem de adada kadınlar kocalarının olmadığı ve diğer erkeklerin bulunduğu ortamlarda kalamayacaklar. Kadınları ve kocalarını da sırasıyla ve harfleriyle gösterelim. Kasabadan adaya gidişi → sembolüyle, adadan kasabaya dönüşü de ← sembolüyle ifade edelim. Çözüm on bir adımda yapılabilir ve aşağıdaki tablodaki gibidir.
Bu çözümden daha kısa bir çözüm vardır. Dokuz adımda sonuçlanan bu çözümü meraklı okurlar kolaylıkla bulabilir.
İkinci Bilmece. Bu bilmecede de üç evli çift bir sahil kasabasının karşısındaki adaya sadece iki kişi taşıyabilen bir sandalla gidecektir. Ama bu kez kadınlar kendi kurallarını koyarlar, kocaları yokken diğer erkeklerin bulunduğu ortamda bulunmamayı kabul etmezler. Kadın dayanışması sonuç verir ve erkeklerin olası baskılarına karşı şu kuralı kabul ettirirler: Her iki tarafta da (kasabada ve adada) kadınlar erkeklerden daha az sayıda olmamalıdır. Ama eğer herhangi bir tarafta hiç kadın yoksa erkeklerden en az biri bulunabilir. Bu altı kişi, bu koşullar altında en az kaç seferde kasabanın karşısındaki adaya geçebilir?
Çözüm. Söz konusu geçiş en az on bir adımda gerçekleşebilir. En uygun geçiş için gereken hamleleri deneme yoluyla bulabiliriz, ama biz ’lük bir matris kullanarak şık bir çözüm vereceğiz.
Kadınların sayısını k, erkeklerin sayısını da e ile gösterelim. k ve e’nin eşit olabileceği sayılar 0,1,2 veya 3 ’tür. Bu durumda ortaya çıkabilecek 4 X 4 = 16 seçenek vardır. Bu seçenekleri 4 X 4’lük bir matrise Şekil-1’deki gibi yerleştirelim. Karelerin içindeki bu sayılar sahil kasabasındaki sırasıyla erkek ve kadın sayılarını göstermektedir. Örneğin “2-1” kasabada 2 erkeğin, 1 kadının bulunduğunu gösteriyor. Tabii ki bu durumda adada 1 erkek 2 kadın bulunmuş oluyor.
Bu 16 seçenekten 6 tanesi bizim istemediğimiz durumlardır, yani “her iki tarafta da (kasabada ve adada) kadınların sayısı erkeklerin sayısından az olmamalı” koşuluna uymamaktadır. (Hiçbir kadının bulunmadığı durumlar dışında). İstenmeyen bu 6 durumun gösterildiği kareleri Şekil-2’de griye boyadık.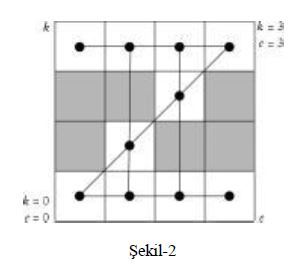
Burada Şekil-1’deki karelerin içindeki sayıların kasabadaki erkek ve kadın sayısını gösterdiğini hatırlatalım ve istenmeyen durumları belirlerken adadaki erkek ve kadın sayısını da dikkate aldığımızı belirtelim. Örneğin Şekil-1’de griye boyadığımız “1-2” karesi bize kasabada 1 erkek ve 2 kadının bulunduğunu gösteriyor, ama bu durumda adada ise 2 erkek, 1 kadın olacağından, yani kadın sayısı erkek sayısından az olduğundan istenmeyen bir seçenektir.
Şekil-2’de griye boyanmayan, kabul edilebilir olan 10 kare içinde hareket ederek problemin çözümünü yapabiliriz. Ama bu hareketleri şu kurallara göre yapmalıyız:
1) Hedefimiz, başlangıç karesi (3-3) olan sağ üst köşeden bitiş karesi (0-0) olan sol alt köşeye bir yürüyüş gerçekleştirmek. Böylece bütün kadın ve erkekler kasabadan adaya taşınmış olacak. Geçtiğimiz bir kareden bir daha geçebiliriz, gri karelerin üstünden atlayarak hareket edebilir, ama gri kareleri kullanamayız.
2) Üzerinden geçebileceğimiz 10 kare var. Bu karelerden sola, sağa, aşağı ve yukarı hareket ederek geçeceğiz. Sandal, kasabadan adaya gidip geri döneceğinden aşağı veya sola olan hareketler yukarı veya sağa olan hareketlere karşılık gelmek zorunda; çünkü aşağı ya da sola olan her adım kasabadan adaya geçişi, yukarı ya da sağa olan her adım da adadan kasabaya geçişi ifade edecek. Örneğin iki kare sola gidersek kasabadan adaya iki kişi taşıyan sandal geri dönerken bir kare sağa gittiğimizde adadan kasabaya bir kişi taşımış olacak. Çapraz gidişlerde ise iki yolcu taşınabilecek.
Bu kurallara göre sorunun çözümünü yapmak zor değil. Böylece problemin sadece dört çözümünün olduğunu görülebilir, yani başlangıç karesinden bitiş karesine belirlediğimiz kurallara göre dört farklı şekilde ulaşabiliriz. Bu dört çözümden biri Şekil-3’te görülmektedir. Meraklı okur diğer çözümleri kolaylıkla bulabilir.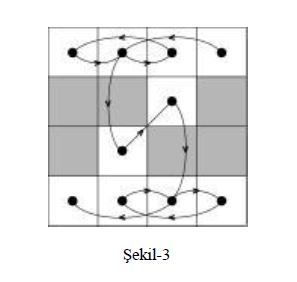
On bir adımda gerçekleşen bu çözümde hareketler Şekil-3’te görüldüğü gibi ilk olarak 3-3 karesinden başlayıp 1-3 karesine gidiyor, ardından 2-3 karesine dönüp ve daha sonra 0-3 karesine giderek devam ediyor. Şekil-3’te oklarla gösterdiğimiz bu hareketleri sıralayalım: (3-3), (1-3), (2-3), (0-3), (1-3), (1-1), (2-2), (2-0), (3-0), (1-0), (2-0), (0-0). Parantez içindeki bu sayılar her adımda kasabadaki erkek ve kadın (sırasıyla) sayılarını göstermektedir. Bu sayıları üçe tamamlayarak her adım için adadaki erkek ve kadın sayısını da bulabiliriz.
Bu çözümü bir de klasik gösterimle ifade edelim: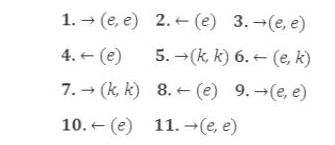
KAYNAKLAR
1) Petkovic, M, Famous Puzzles of Great Mathematicians, AMS, 2009.
2) Gardner, M, The Last Recreations: Hydras, Eggs, and Other Mathematical Mystifications, Springer, 2007.










