Matematikte doğruluğu kanıtlanabilen önermelere teorem deniliyor. Tarih boyunca matematiğin inşası süresince binlerce önerme kanıtlandı, kanıtlanıyor. En önemli, en iz bırakan ve bir kilometre taşı olarak görülebilecek teoremler hangileridir? Bu soruyu matematikle uğraşan hemen herkes farklı listeler yaparak yanıtlayabilir.
En iyi 100 film, en iyi 100 roman gibi matematiğin en büyük 100 teoreminin listesi matematikçiler Jack ve Paul Abad tarafından oluşturulup, 1999’daki bir matematik konferansına sunuldu.(1) Abad’lar listeyi hazırlarken şu üç kriteri kullandıklarını açıkladılar: Teoremin literatürdeki önem ve yeri, kanıtın kalitesi ve doğurduğu sonuçlar.
Yukarıdaki kriterlere ek olarak, teoremi ortaya atan veya kanıtlayan matematikçinin tanınırlığını, büyük matematikçi olmasını da dikkate alarak daha dar ve popüler bir liste Amerikalı matematik tarihçisi William Dunham tarafından oluşturulmuş.(3)
Büyük matematikçilere ait teoremleri önemsemek gerektiğini düşünüyorum, çünkü nasıl ki edebiyat tarihinin en önemli eserlerinden söz edilirken Dostoyevski, Balzac gibi dev yazarların isimlerinin geçmemesi mümkün değilse, teoremlerle ilgili bir listede de Newton, Euler, Gauss gibi büyük matematikçilerin yer alması son derece doğal.
Kuşkusuz ki, matematiğin büyük teoremlerinin listesi her matematikçi için keyfi bir seçimle farklı teoremleri kapsayacaktır. Aşağıdaki liste de yukarıda saydığımız özellikleri taşımakla birlikte eksiktir. Öte yandan okuru matematik tarihinde küçük bir geziye çıkarmayı amaçlayarak kronolojik bir liste yapmaya çalıştım.
Teoremlerin kanıtlarını bu yazının kapsamı içinde vermem mümkün olmadığından meraklı okur için her teoremin kanıtının yer aldığı kaynakları yazının sonunda belirttim.
Hilalin kareleştirmesi
Antik Çağ Yunan matematiğinin önemli problemlerden biri “dairenin kareleştirilmesi”, yani bir dairenin alanına eşit olan bir karenin pergel ve cetvel kullanılarak çizimidir. Sakızlı Hipokrat (MÖ 440) (Hekim olan Koslu Hipokrat’la karıştırılmamalı.) bu problemle uğraşırken hilallerin (aycıklar) kareleştirilmesini başarmış, yani hilalle eşit alanlı bir kare inşa etmiştir.
Aşağıdaki şekilde O merkezli AC çaplı ve D merkezli AB çaplı yarım dairelerle oluşan AFBE hilalinin alanının AOB ikizkenar dik üçgenin alanına eşit olduğunu kanıtlayan Hipokrat, bu üçgenin alanının iki katına karşılık gelen bir kareyi oluşturarak hilali kareleştirmiştir.(2)
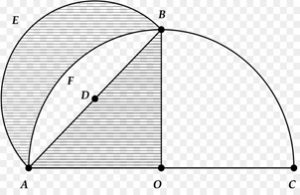
Hipokrat, hilallerin alanlarıyla ilgili yukarıdakine benzer çok sayıda örnek vererek matematikçiler arasında dairenin kareleştirilmesi probleminin çözümü için iyimser bir hava yaratmıştır. Binlerce yıl birçok matematikçinin bu yönde çalışmış olmasına karşın sonuç alınamamıştır. Bu problemin çözümsüz olduğu yaklaşık 2000 yıl sonra, 1882’de Alman matematikçi Ferdinand von Lindemann (1852-1939) tarafından gösterilmiştir.Lindemann, Pi sayısının “aşkın” bir sayı (katsayıları rasyonel sayı olan bir polinomun kökü olmayan reel sayı) olduğunu kanıtladığından, pergel ve cetvelle bir kenarı Pi’nin karekökü olan bir karenin inşa edilemeyeceği sonucuna ulaşılmıştır.
Öklid’in Elemanları’nda yer alan Pisagor Teoremi’nin ispatı
Öklid’in (M.Ö 330-270) kendinden önceki matematikçilerin eserlerini ve öz çalışmalarını derleyerek oluşturduğu Elemanlar isimli kitabı matematiği, hatta bilim ve felsefeyi olağanüstü etkilemiştir. 13 kitapta 465 önermenin yer aldığı bu yapıt, tanım, önerme ve ispatlardan oluşanaksiyomatik sistemin temellerini atarak teorik matematiğinbaşlangıç metni olarak kabul edilir.
Elemanlar’ın 1’inci kitabının 47’inci önermesi Pisagor Teoremi’dir: Dik açılı üçgenlerde dik açıyı gören kenar üzerindeki kare, dik açıyı içeren kenarlar üzerindeki karelere eşittir.
Öklid, Pisagor Teoremi’ni bu önermeden önce ifade ettiği tanım, önerme ve teoremlere dayanarak müthiş bir titizlikle kanıtlamıştır.[3]Yukarıdaki şekil yardımıyla yapılan bu kanıt Pisagor Teoremi’nin bilinen ilk yazılı kanıtı olmakla birlikte, aksiyomatik yöntemin en çarpıcı örneğidir.
Asal sayılar sonsuz sayıdadır
Bu teorem sayılar teorisinin temel bir önermesidir ve sonsuz sayıda asal sayının olduğunu ifade eder. Öklid bu teoremi Elemanlar’ın 9. kitabının 20. önermesi olarak ifade etmiş, her sonlu asal sayı listesi için bu listede bulunmayan başka bir asal sayının olacağını, bu yüzden de asal sayıların sonsuz sayıda olduğunu göstererek kanıtlamıştır.[,(3)
Öklid’in çelişki yaratma yoluyla (olmayana ergi) yaptığı bu kanıt birçok matematikçi tarafından en güzel kanıtlardan biri olarak gösterilmiş ve bu teorem daha sonra birçok farklı yolla kanıtlanmıştır.
√2 irrasyonel sayıdır
Dünyanın ilk matematikçilerinden biri olan Pisagor (Pythagoras) (MÖ 572-497) “Tanrı sayıdır” diyordu ve sayı olarak sadece doğal sayıları kabul ediyordu; kurduğu okulda evrenin, doğal sayılar ve onların oranları kullanılarak oluştuğu öğretiliyordu.
√2 irrasyonel bir sayıdır teoremi Pisagorcuların kâbusu olmuştur. Bu olayın ilginç hikâyesini daha önce bu köşede anlatmıştık.(8)
√2’nin rasyonel olmadığının ilk yazılı kanıtı yine Öklid’in Elemanlar’ında (2) (10’uncu kitap önerme 117) verilmiştir. Bu teoremin kanıtında da olmayana ergi yöntemi kullanılmış, √2’nin rasyonel olduğu, iki tamsayının oranı olarak yazılabileceği kabul edilmiş, çelişkili bir sonuçla teoremin doğruluğu gösterilmiştir.
Bu kanıt irrasyonel sayılar kümesinin varlığının habercisi olduğu için sayılar teorisi için ayrı bir öneme sahiptir.
Arşimet’in dairenin alanını hesaplama yöntemi
Arşimet’in (MÖ 287-212) gelmiş geçmiş en büyük matematikçilerden biri olarak görülmesi boşuna değildir. Ona bu payenin verilmesi birçok kavramı ilk kez bilimsel incelemeye tabi tutmuş olmasından kaynaklanır. Alan ve hacim hesaplarında kullandığı yöntemler yüzyıllar sonra Newton ve Leibniz’indiferansiyel ve integral hesabı keşfetmesine ilham kaynağı olmuştur.
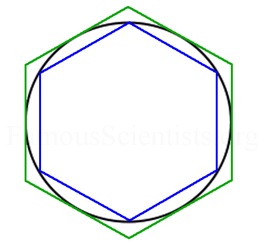
Arşimet’in bir dairenin düzgün dış teğet çokgeniyle dairenin içine çizilen düzgün kiriş çokgeninin alanlarını hesaplayarak dairenin alanını bulma çabası π sayısının değerinin 3 10/71 sayısıyla 3 1/7 sayısı arasında olduğunu göstermiştir.
Aşağıdaki şekilde dairenin içine ve dışına çizilmiş iki altıgen görülüyor. Dıştaki altıgenin alanı dairenin alanından büyük içtekininse küçüktür. Arşimet, bu çokgenlerin kenar sayısını 12, 24, 48 ve son olarak 96 alarak sayısının değer aralığını saf bir zihin gücüyle bulmayı başarmıştır.(2)
Üçgenin alanı için Heron formülü
Üç kenar uzunluğu bilinen bir üçgenin alanı veren bu formül İskenderiye’li geometrici, mekanikçi Heron’un (M.S 75) Metrica isimli kitabında yer almıştır. Kenar uzunlukları olan bir üçgenin alanı u= (a+b+c)/2 olmak üzere √(u(u-a)(u-b)(u-c)) olarak hesaplanmıştır.
Bu formülü listeye “büyük teorem” olarak almamızın nedeni, formül sayesinde üçgenin alanınınpratik yoldan bulunuyor olmasının yanı sıra, kanıtındaki adımların mükemmel bir soyutlamayla geometrik akıl yürütmeye sahip olmasıdır.
Bundan sonraki başlıkta yer alan teoremin ortaya çıkışıyla yukarıdaki arasında yaklaşık 1500 yıl geçmiştir. Bilindiği gibi bu dönemde Hint ve İslam matematikçilerinin çalışmaları ön plandadır. Musa al-Harezmi (780-850), Sabit bin Kurra (826-901), Ömer Hayyam (1048-1131), Şarafeddin Al-Tusi(1135-1213), Nasireddin Al-Tusi (1201-1274) Cemşit Al-Kaşi (1380-1429) gibi birçok bilgin ve matematikçilerin küresel geometriye, cebire, sayılar teorisine, trigonometri ve astronomiye özgün ve önemli katkıları olmuştur.[3] Ama bu çalışmalar birçok nedenden dolayı matematik literatüründe “teorem” olarak yer alamamıştır. Örneğin Şerafeddin Al-Tusi üçüncü dereceden denklemlerin çözümünü araştırırken “türevi” tanımlamış, ama türev, sonrasında Fransız matematikçi Fermat ve daha sonra da Newton ve Leibniz tarafından keşfedilerek literatüre girmiştir.
Üçüncü dereceden denklemlerin çözümü
İkinci dereceden denklemlerin kısmi çözümü (pozitif köklerin bulunması) MÖ 2000-1000’lerde Babilliler tarafından biliniyordu; fakat üçüncü dereceden denklemlerin genel çözümünün keşfi, o tarihten sonra insanlığın en az 2500 yılını almıştır.
Üçüncü dereceden denklemlere Antik Yunan’da bazı özel çözümler yapılmış, sonrasında Ömer Hayyam, Şerafeddin Al-Tusi gibi matematikçiler kısmi çözümlere ulaşmıştır. Özellikle İran’lı şair ve matematikçi Hayyam, 1075 yıllında yayımladığı Cebir Problemleri ve Karşıtlık Kanıtları Üzerine adlı eserinde geometrik yapıları (konik kesitlerinin kesişim noktalarını) kullanarak bu yolda önemli adımlar atmış; ama kökleri katsayılara bağlı olarak ifade edemeyip, bunu geleceğin matematikçilerinin başarması temennisinde bulunmuştur.
1535’te her şey değişmiş, Hayyam’ın temennisi gerçekleşmiştir. İtalyan matematikçi NiccolòTartaglia(1499-1557) a≠0 olmak üzere
ax^3+bx^2+cx+d=0
denklemini katsayılarına bağlı olarak çözmüştür.(3)
Tartaglia’nın çözümü matematik literatürüne Cardano formülleri ismiyle geçmiştir; çünkü Milano’lu bilgin Gerolamo Cardano (1501-1576) Tartaglia’nın bir sır gibi sakladığı çözümü Tartaglia’dan öğrenip, açıklamayacağına dair söz vermiş olmasına karşın Ars Magna isimli eserinde yayımlamıştır.(4)
Cardano, Ars Magna’da üçüncü dereceden denklemlerin kökleri arasında karesi negatif sayı olan sayıların da varlığına dikkat çekerek karmaşık sayılar kuramının işaret fişeğini ateşlemiştir.
Newton’un alan hesaplama yöntemi ve π sayısı
Isaac Newton ( 1643– 1727) önce Newton’un Binom Teoremi adıyla bilinen teoremi formüle etmiş ve sonrasında da mükemmel bir yöntemle eğri altında kalan alan hesabını keşfetmiştir.
Newton, merkezi 1/2,0) ve yarıçapı 1 birim olan çember x=1/4 doğrusunu ve x ekseni arasında kalan bölgenin alanını √(1-x)’i seriye açarak hesaplamış ve π sayısının 16 basamağını bulmuştur.(3)
Ters karelerin toplamı
Basel problemi adıyla bilinen bu teorem Pietro Mengoli tarafından 1644’te ortaya atılmış ve yaklaşık yüzyıl sonra 1735 yılında Leonhard Euler (1707-1783) tarafından çözülmüş ünlü bir sayı kuramı problemidir. Bu problem sayma sayılarının karelerinin çarpmaya göre terslerinin toplamından oluşan aşağıdaki serinin hangi sayıya yakınsadığını sormaktadır.
1/1^2 +1/2^2
Jacob, Johann ve Daniel Bernoulli gibi matematikçileri yaklaşık bir asır boyunca uğraştıran bu serinin Euler π^2/6’ya yakınsadığını göstererek 28 yaşında büyük ün sahibi olmuştur.(3) Euler’in seri üzerinde yaptığı bazı oynamalar zamanın matematikçilerince kabul görmemiş ve Euler daha kesin sonuçlar veren kanıtını 6 yıl sonra 1741’de tamamlayarak problemi genelleştirmiştir. Onun düşünceleri Bernhard Riemann’ın 1859’da yazdığı “Belirli Bir Büyüklükten Küçük Asal Sayılar Üzerine” isimli makaleye esin kaynağı olmuştur.
Cebirin Temel Teoremi
Bu teorem karmaşık değişkenli polinomların varlığıyla ilgili temel bir sonuçtur. Teoremin açık ifadesi şöyledir: Katsayıları karmaşık sayı olan ve sabit olmayan tek değişkenli her polinomun en az bir (karmaşık) kökü vardır.
Teoremi önce d’Alembert (1717-1783), Euler ve Daniel Bernoulli kanıtladıklarını açıklamışlar ama bu kanıtların yanlış olduğu anlaşılmıştır. 1799’da Carl Friedrich Gauss (1777-1855) geometrik bir kanıt vermiştir, ama bu kanıtta da topolojik bir hata ortaya çıkmıştır. İlk doğru kanıtı 1806’da kitapçı ve matematikçi Jean Robert Argand (1768-1822) tarafından bulunmuştur. Gauss
1816’da teoremin iki değişik kanıtını vermiş ve daha sonra 1849’da ilk kanıtı düzeltmiştir. O gün bugün teoremin birçok değişik kanıtı yapılmıştır.(5)
Cebirin Temel Teoremi günümüzde cisimler teorisinden spektral analize kadar birçok teorinin temelinde yer alan bir teoremdir.
Cantor Teoremi
Alman matematikçi Georg Cantor (1845-1918) sonsuz kümeler kuramını inşa ederek matematikte devrim niteliğinde adımlar atmıştır. Matematik literatürüne Cantor Teoremi adıyla geçen önerme, boş olmayan herhangi bir A kümesinin kuvvet kümesinin gücünün (kardinalitesinin), A kümesinin gücünden büyük olduğunu söyler. Kuvvet kümesi P(A) gösterilirse, teoreme göre A kümesi ile P(A) arasında birebir eşleme yapılamaz.
Cantor’un 1891’de kanıtladığı bu önerme sonlu kümeler için bariz bir sonuç olsa da sonsuz kümeler için çığır açıcı sonuçlar doğurmuştur.
Gödel’in Eksiklik Teoremleri
Avusturyalı mantıkçı ve matematikçi Kurt Gödel (1906-1978) matematiğin mantıksal olarak tutarlı olduğunu kanıtlamanın mümkün olmadığını kanıtlayarak matematiğin temellerine olan bakışı kökten değiştirmiştir. Gödel, aksiyomatik bir sistemin tutarlı ise eksiksiz olamayacağını göstermiş ve ayrıca aksiyomatik bir sistemin tutarlılığını sistemin kendi içindeki adımlarla kanıtlamanın olanaksız olduğunu ispatlamıştır.(7)
Gödel’in eksiklik teoremleri matematikten felsefeye ve yapay zekâya kadar birçok alanda önemli sonuçlar doğurmuştur.
KAYNAKLAR
1) http://pirate.shu.edu/~kahlnath/Top100.html
2) Öklid’in Elemanları, Çev. Ali Sinan Sertöz, Tübitak Yayınları,
3) 2019.http://jwilson.coe.uga.edu/emt725/References/Dunham.pdf
4) https://bilimvegelecek.com.tr/index.php/2018/1/31/matematiksel-duello/
5) Carl Friedrich Gauss, Cebirin Temel Teoremi İçin Dört İspat, Boğaziçi Üniversitesi Yayınevi,Çev. Gülnihal Yücel, 2015.
6) http://mat.msgsu.edu.tr/~dpierce/Dersler/Kumeler-kurami/2015/kumeler-kurami-2016-02.pdf (S.107)
7) James R. Newman, Ernest Nagel, Gödel Kanıtlaması, Boğaziçi Üniversitesi Yayınevi, 2008.
8) https://bilimvegelecek.com.tr/index.php/2018/01/01/%e2%88%9a2-krizi/










