Bir pastayı (ya da bir somun ekmeği) arkadaşınızla paylaşacaksınız ve elinizde sadece bir bıçak var. Her iki tarafın da gönül rahatlığıyla kabul edeceği bir paylaşım nasıl yapılabilir? Popüler matematik meraklılarınca iyi bilinen bu sorunun yanıtı çok basit: Arkadaşınıza “Sen kes, ben seçeyim” önerisinde bulunursunuz, olur biter. Böylece artık onun amacı (kendine göre) pastayı eşit iki parçaya bölmektir, çünkü seçimi siz yapacaksınız. Eğer siz parçaların eşit olmadığını düşünüyorsanız büyük olanı seçersiniz. Bu durumda arkadaşınız sonuçtan memnun değilse, pastayı daha dikkatli kesmesi gerektiğini ve şikâyet etme hakkının olmadığını düşünmelidir. Eğer bu paylaşımdan siz memnun değilseniz, o zaman yanlış dilimi seçmişsiniz demektir. Sonuçta iki taraf da adil bir paylaşım yapılmadığını iddia edemez. Eğer başlangıçta arkadaşınız pastayı kesmeyi değil, seçmeyi tercih ederse bu kez sadece roller değişir, yine aynı yöntemle adil bir paylaşım yapılabilir.
Kısaca “kes ve seç” olarak adlandıracağımız bu yöntemin şu özellikleri sağladığını görüyoruz:
1) Kıskançlık yok. İki taraf da paylarına düşen parçaların en büyük parçadan daha küçük olmadığını düşünür ve karşısındakini kıskanmaz.
2) Verimli. Tarafların birbirlerine zarar vermediği bu paylaşımdan daha iyi bir dağılım yapılamaz.
Bu yöntemin sağlamadığı bir özellik eşitliktir. İki taraf da kendi paylarını sübjektif ölçülerle belirlediklerinden mutlak bir eşitlikten söz edilemez.
Çikolatalı ve vanilyalı pastanın paylaşımı
Şimdi, problemi biraz zenginleştirerek pastanın sol yarısının vanilyalı, sağ yarısının da çikolatalı olduğunu varsayalım. A ve B gibi iki kişiden A kessin, B de seçsin, ama ayrıca A için vanilyalı pasta kakaoluya göre iki kat değerde olsun. “Kes ve seç” paylaşımı nasıl yapılabilir? (Kaynak 1)
Bu durumda A, tabii ki payını pastanın sol yarısından almak isteyecektir, ama seçimi B yapacağından “adil” bir kesim yapmayı amaçlamalıdır. A, bu kesimi vanilyanın çikolatanın 2 katı değere sahip olduğunu düşünerek yapacağından pastayı tam ortadan kesmeyecektir. Onun için “adil” olan, yani onun ölçülerine göre yarı yarıya olacak paylaşım pastanın vanilyalı tarafında ve yarım porsiyondan küçük olmalıdır.
Pastanın, soldan sağa doğru sayı doğrusu üzerinde [0, 1] aralığındaki sayılarla temsil edildiğini düşünelim. [0, 1/2] aralığı vanilyalı, [1/2, 1] aralığı da çikolatalı bölümü göstersin. Bu aralıkta alacağımız herhangi bir reel sayı A’nın pastayı hangi oranda keseceğini ifade eder, ama unutmayalım A için vanilyalı bölüm çikolatalı bölümün iki katı değerinde. Bu durumda A’nın hangi oranda pastayı keseceğini gösteren sayı x ise x ≤ 1/2 olacaktır.
![]()
Buna göre aşağıdaki denklemi yazabiliriz:
2x=2(1/2-x)+1-1/2
A’ya göre pastanın ilk yarısından aldığı 3/8’lik dilim her iki taraf için adil ve eşit bir paylaşımı ifade ediyor, çünkü A vanilyaya çikolataya göre 2 kat değer biçiyor.
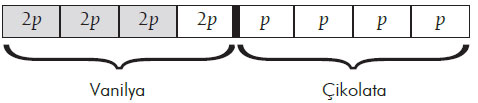
Tabloda da görüldüğü gibi A, griye boyalı olan 6p’lik bölümü almayı amaçlıyor ve B’ye de yine 6p’lik bölüm kalıyor.
Bir kez daha hatırlamakta fayda var: Bu paylaşımda iki porsiyonun eşitliği A’nın pastaya biçtiği değere göre belirleniyor ve A’nın bu değerlendirmesinden B’nin haberi yok. Eğer B, vanilya ve çikolataya eşit değer veriyorsa, bu durumda 5/8’lik porsiyonu tercih ederek büyük parçayı almış olacak. Bu paylaşım B’yi mutlu edecek çünkü kendini A’ya göre daha iyi durumda görecek. Öte yandan A da amacına ulaşmış olacak ve kendi açısından hakkaniyetli bir dağılımın yapıldığını düşünecektir. Dolayısıyla bu paylaşım “kes ve seç” yönteminin tüm özelliklerini sağlıyor.
Eğer kesme işlemini B yapar, A seçerse yine “kes ve seç” yöntemine uygun bir dağılım yapılacaktır. Şöyle ki: Bu kez B pastayı tam ortadan keserek yarısı vanilyalı, diğer yarısı da çikolatalı olacak şekilde iki eşit porsiyona ayırabilir çünkü onun için her iki bölüm de eşit değerde. Bu durumda A tabii ki vanilyalı bölümü seçecek ve böylece her iki taraf da “kes ve seç” yöntemine göre istediği sonuca ulaşmış olacaktır.
Bu paylaşımın “kes ve seç” yöntemine uygun olarak yapılabilmesi için A’nın pastayı soldan (vanilyalı bölümden) sağa doğru kesme işlemi için belirlediğimiz x sayısı [3/8,1/2] aralığında bulunmalı, yani 3/8 ≤ x ≤ 1/2 olmalı. Bu aralıktan seçilecek her x değeri için her iki tarafı da memnun eden paylaşımlar yapılabilir.
Bu problemi genelleştirmek mümkün, yani vanilya ile çikolata arasındaki değerlerin kişilere göre değişmesi durumunda “kes ve seç” yönteminin nasıl çalışacağı ele alınabilir. Ama biz böylesi bir incelemeyi sonraki yazılara bırakarak, belki de birçok okurun merak etmiş olabileceği “kes ve seç” yönteminin 3 kişi arasındaki uygulamasını ele almaya çalışalım.
Üç kişi için “kes ve seç” yöntemi
Amerika’lı ve İngiliz matematikçiler John Selfridge ve Horton Conway’ın 1960’ların başında A, B, C gibi üç kişi için formüle ettikleri “kes ve seç” yönteminde şu adımlar uygulanıyor:
1) A, pastayı “kes ve seç” yöntemine göre (adil olarak) üç parçaya böler.
2) B, eğer en büyük iki parçanın birbirine eşit olduğunu düşünürse ya sırasını atlar, ya da parçaları eşitlemek amacıyla büyük olandan parça ya da parçalar keser. Adına “artık” diyeceğimiz bu parçalar bir yerde toplanır.
3) C, B ve A, kendilerince en büyük buldukları parçayı belirtilen sıraya göre seçerler. Eğer B ikinci adımda sırasını atlamadıysa dilimleri eşitlemek için küçük parçalar kestiği dilimi seçmek zorunda, tabii daha önce C, o dilimi seçmediyse.
Bu durumda pasta, B’nin kestiği küçük parçalar hariç “kes ve seç” yönteminin özelliklerine uygun olarak paylaşılmış olur.
4) Eğer B, ikinci adımda sırasını atladıysa artık parça bulunmayacağından paylaşım işlemi tamamlanmış demektir. Eğer atlamadıysa C veya B artık parçaları birleştir. Bu oyunculardan biri artık parça yığınını kesecektir. Bu oyuncuyu “kesen” , diğerini “kesmeyen” olarak adlandıralım. “Kesen” artık parça yığınını eşit olduğunu düşündüğü üç parçaya ayırır.
Bu aşamada A’nın durumuna değinelim: A, “kesmeyen” oyuncuya göre başından avantajlı, çünkü A, başlangıçta bütün parçaların eşit olduğunu düşündüğü bir paylaşım yapmıştı ve “kesmeyen” oyuncu küçük parçalar kesildikten sonra kalan parçayı almıştı. Bu yüzden A, “kesmeyen” oyuncunun adil olmayan bir pay almadığını düşünecek ve “artıkların” paylaşılıyor olmasından dolayı “kesmeyeni” kıskanmayacaktır.
5) Üçe bölünmüş artık parçalar oyuncular arasında şu sırayla paylaşılır: “Kesmeyen”, A ve “kesen”. Elbette, her oyuncu kendilerine göre en büyük parçayı seçecektir. Bu paylaşımda “kesmeyen” ilk seçimi yaptığı için kıskanacağı bir durum söz konusu değildir. A, “kesmeyeni” kıskanmaz çünkü daha başlangıçtan avantajlı, “kesen” oyuncudan önce seçim yaptığından onu da kıskanmaz. “Kesen” oyuncu parçaları kendi kestiği için hiç kimseyi kıskanmaz.
Selfridge ve Conway’in üç kişi için geliştirdikleri “kes ve seç” yöntemi daha sonra siyaset bilimci Steven J. Brams ve Alan D. Taylor tarafından dört kişi için de formüle edildi. Sonrasında beş ve daha fazla oyuncu için de kesim sayısı sınırlı olmayan algoritmalar oluşturuldu. Gelecek ayki yazıda bu ilginç konuyu incelemeyi sürdüreceğiz.
Kaynaklar
1) S. J. Brams, Micheal A. Jones, Christian Klamler, Better Ways to Cut a Cake, Notices of the AMS, Volume 53, Number 11, 2006.
2) Ian Stewart, Matematik Histerisi, Çev. A. N. Narman, Aylak Kitap, 2013.