– Harika bir olasılık sorusu öğrendim, hiç hesaplama gerektirmeyen çok zarif ve kısa bir çözümü var: Bir küre yüzeyi üzerinde rastgele 4 nokta seçerek bu noktaları köşe kabul eden bir dörtyüzlü oluşturuyoruz. Kürenin merkezinin bu dörtyüzlü içinde olma olasılığı kaçtır?
– Güzel bir soru, ama kolay değil.
– Çözüm basit bir düşünceye dayanıyor. Bu soruyu Amerika’da düzenlenen Putnam Matematik Yarışmasının ilk bölümünün son sorusu olarak sormuşlar, yani en zor sorulardan biri. Ne diyorsun, çözebilir misin? Hatırlarsan bir zamanlar bana sorduğun bir olasılık sorusunu anında yanıtladığımda cevabımın doğru ama çözümümün yanlış olduğunu söylemiştin. “Nasıl çözdüğümü bilmiyorsun ki, neden yanlış?” diye sorduğumda, “Basit bir çözüm yaptığını anladım, matematikte çözüm basitse yanlıştır” diyerek dalga geçmiştin. Şimdi bu kez ben soruyorum ve oldukça basit bir çözümün olduğunu söylüyorum, bakalım bulabilecek misin? Bir saat süre, ama internete başvurmak yok!
– Anlaşıldı, geçmişin intikamı! Peki, bir saat sonra görüşelim.
Yukarıdaki diyalog yeğenim Doğucan Gün-cü’yle yaptığımız bir telefon görüşmesinde geçti. Bir saat sonra aradı. Çözememiştim. Güzeli görmenin heyecanı ve keskin zekâsıyla çözümü anlattı. Gerçekten çok hoş ve yalın bir akıl yürütmeyle gerçekleşen bu çözümü Bilim ve Gelecek okurlarıyla paylaşmak istedim.
Problemi bir kez daha ifade edelim: Küre yüzeyinde rastgele alınan dört noktayla bir dörtyüzlü oluşturuyoruz ve kürenin merkezinin bu dörtyüzlünün içinde olma olasılığını bulmak istiyoruz. Örmeğin aşağıdaki şekilde sağdaki dörtyüzlü kürenin merkezini kapsıyorken, soldaki kapsamıyor.
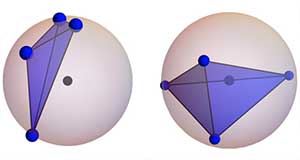Matematikte bir problemi çözerken daha basit bir analog problem bularak çözüme ulaşmak çok sık kullanılan bir yöntemdir. Biz de bu problemi şimdilik bir kenara bırakıp, bu sorunun çember versiyonuna bakalım.
Bir çember üzerinde rastgele üç nokta alarak bu noktaları köşe kabul eden bir üçgen oluşturuyor ve şu soruyu soruyoruz: Çemberin merkezinin üçgenin içinde olma olasılığı kaçtır?
Çözüm oldukça basit ve akıl dolu: Önce, çember üzerinde rastgele üç nokta seçmek yerine rastgele bir şekilde [BB’] ve [CC’] çaplarını çizelim ve çember üzerinde sadece bir noktayı sabitleyelim. Bu noktayı A ile gösterirsek, A noktası [BB’] ve [CC’] çaplarının çember üzerinde ayırdığı 4 farklı yaydan birinin üzerinde olacaktır, dolayısıyla A’yı herhangi bir yere koyabiliriz, BC (kısa) yayı üzerinde olsun. Bu durumda artık diğer iki noktanın sabitlenmesi için 4 farklı seçim yapabiliriz, şöyle ki: noktalardan birini B veya B’ diğerini ise C veya C’ noktalarından seçmeliyiz, yani, 2×2=4 farklı seçim yapabiliriz: B–C, B’–C, B–C’, B’–C’. Böylece A dışındaki iki noktayı 4 farklı şekilde sabitleyeceğimizi görmüş olduk, şimdi artık ABC, AB’C, ABC’ ve AB’C’ üçgenlerini çizebiliriz. Aşağıdaki şekilde bu 4 üçgen görülmektedir. Bu üçgenlerden sadece AB’C’ üçgeni çemberin merkezini kapsıyor. O halde çember üzerinde rastgele alınan 3 noktayı köşe kabul eden üçgenin çemberin merkezini kapsaması olasılığı 1/4’tür. Mükemmel bir çözüm!
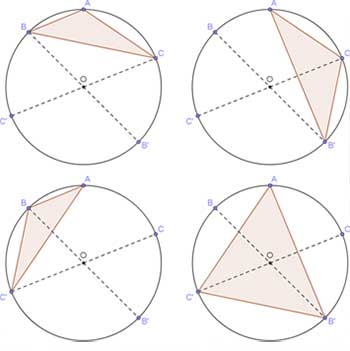Asıl sorumuza, küre yüzeyinde rastgele alınan 4 nokta problemine geri dönelim ve yukarıda ulaştığımız bulguları bu problemin çözümünde kullanalım.
Çemberin 2 farklı çapını çizmiştik, bu kez kürenin 3 farklı çapını çizerek çözüme başlayalım. Bu çapları [AB], [CD], [EF] ile gösterirsek her bir çapı kapsayan üç düzlemle küre sekiz parçaya bölünmüş olacaktır. Aşağıdaki şekle bakıp, bu küre parçalarını hayal etmemiz mümkün.
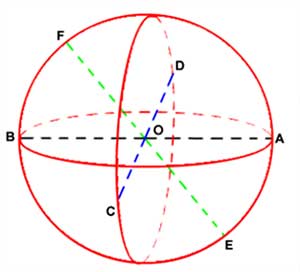Şimdi, tıpkı çemberin çaplarının uç noktalarını seçtiğimiz gibi burada da 3 çap için 2×2×2=8 farklı seçim yapabiliriz, şöyle ki A ya da B’yi veya C ya da D’yi veya E ya da F’yi seçebiliriz. Böylece 4 noktanın 3’ünü sabitlemiş oluruz. Bu 8 seçeneğin ortaya çıkardığı üçgenleri şu şekilde sıralayabiliriz: ACE, ACF, ADE, ADF, BCE, BCF, BDE, BDF. Dördüncü nokta sekiz küre parçasından herhangi biri üzerinde olabilir. Bu noktayı P ile gösterip, AE yayının arka tarafındaki küre parçasının üzerine koyduğumuzu varsayarsak (P, BCF) dörtyüzlüsü kürenin merkezini kapsarken diğer dörtyüzlüler merkezi kapsamayacaktır. Çünkü P noktasını BCF üçgeninin tam karşısındaki bölgeye koymuş olduk; bu durum diğer üçgenler için geçerli olmadığı için sadece (P, BCF) dörtyüzlüsü merkezi kapsıyor. Böylece küre üzerinde rastgele seçilen 4 noktayı köşe kabul eden dörtyüzlünün kürenin merkezini kapsama olasılığı 1/8 olarak bulunur.
Ne kadar ince ve zekice bir yol, değil mi? Çözüm çok basit ve yanlış değil! Öte yandan, problemi önce iki boyutta ele alıp, oradaki yöntemi üç boyuta taşımak da mükemmel bir hamle! Burada ister istemez şu soru geliyor insanın aklına: İki boyutta olasılık 1/4, üç boyutta 1/8 olduğuna göre dört boyutta(!) 1/16 mı olur? Böylesi bir problemi ortaya koyup çözmeden “1/16 olur” diyemeyiz elbette, ama problemi bir boyuta indirgersek bu kez sonuç 1/2 oluyor, şöyle ki: “[0,1] aralığından rastgele iki reel sayı alırsak sıfır sayısının bu sayılar arasında kalma olasılığı kaçtır?” diye soralım ve şöyle düşünelim: Sayılardan birini 0’ın soluna ya da sağına koyma olasılığı 1/2’dir, artık diğer sayının diğer tarafta olma olasılığı 1 olacağından sonuç 1/2’dir. Dolayısıyla üç boyuta kadar boyut sayısına bağlı olarak istenen olasılık 1/2n formülüyle hesaplanabiliyor. Sonrasını bilmiyoruz!
Not: Meraklı okur www.brilliant.org adresinden bu problemin çözümünün üç boyutlu simülasyonunun yer aldığı videoyu izleyebilir.
