Evlilik gibi karmaşık bir meseleyi matematiksel açıdan incelemek merak uyandırıcı. Yazının başlığından hareketle, mantık ve duygu savaşına nihayet bir çözüm getirildiği, evliliğin iyi olup olmadığı hususunda matematiğin son sözü söylediği düşünülebilir. Bu tür heyecanlara kapılmak yerine evlilik ve benzeri konuların matematik problemlerine nasıl dönüştüğüne, bilim dünyası için ne anlama geldiğine odaklanmalı.
Evlilik gibi karmaşık bir meseleyi matematiksel açıdan incelemek merak uyandırıcıdır. Yazının başlığından hareketle, mantık ve duygu savaşına nihayet bir çözüm getirildiği, evliliğin iyi olup olmadığı hususunda matematiğin son sözü söylediği düşünülebilir. Bu tür heyecanlara kapılmak yerine evlilik ve benzeri konuların matematik problemlerine nasıl dönüştüğüne, bilim dünyası için ne anlama geldiğine odaklanmak gerekiyor.
Üniversite yerleştirme ve oda arkadaşı problemleri
Eğitim sisteminin eleştirisini bir yana bırakarak, öğrencilerin lise eğitimini tamamladıktan sonra üniversite sınavlarına girdiği gerçeğine dönelim. Adaylar tercih listeleri yaparak üniversite yerleştirme sonuçlarını beklerler. ABD’de olduğu gibi, örneğimizdeki üniversitelerin de adaylar arasında seçim yapma hakları olsun. Adaylara a ve b, üniversitelere ise A ve B diyelim. a’nın A’ya, b’nin ise B’ye yerleştirildiği bir durum düşünelim. Gerçekte b’nin A’yı, A’nın da b’yi istediği bilgisine sahipsek, bu eşleştirmenin kararsız olduğunu söyleyebiliriz, çünkü b ile A birbirini istemekte ve böylesi bir eşleştirmeyi kendi açılarından gelişim olarak görmektedir.
Kararlı, denge hâlindeki bir eşleştirmenin ne olduğunu bir başka örnekle açıklayabiliriz. Çift sayıda erkeğin oda arkadaşlığı için listeler hazırladığını düşünelim. Kararlı bir eşleştirme için, oda arkadaşı olmayan ve birbirlerini mevcut oda arkadaşlarına tercih eden iki erkeğin bulunmaması gerekir. Örneğin A, B, C ve D isimli dört erkeği bir öğrenci yurduna yerleştirmemiz istendi. A’nın ilk tercihi B, B’ninki C ve C’ninki A olsun. A, B ve C’nin son tercihinin D olduğu bir durumda, D’nin tercih sırasından bağımsız olarak, kararlı bir eşleştirme yapılamayacağı ortaya çıkar. Kanıt için kâğıt üzerinde kısa bir liste yapmak yeterlidir.
Köyün gençleri ve evlilik
Yukarıdaki iki probleme benzer şekilde ele alacağımız esas örneğimiz evlilikle ilgili olandır. Konuyu daha keyifli bir hâle getirmek için Ali Nesin’in Evliliğin Matematiği isimli çalışmasından yararlanacağım. (1)
Köyün birinde, evlenme çağındaki gençler her yılbaşında, evlenmek istedikleri kişilerin isimlerini bir listeye yazar ve ihtiyar heyetine verirmiş. Heyetin haftalar süren çalışmaları neticesinde gençler arasında bir eşleştirme yapılırmış. Heyet bu işte öylesine başarılıymış ki hiç boşanma görülmezmiş. Bir başka deyişle, bir erkek ve kadının eşlerinden ayrılıp birbirleriyle evlenmek istedikleri bir durum hiç olmazmış, biri istese diğeri istemezmiş. Gel zaman git zaman, heyettekiler bir konuda şüphe duymaya başlamış ve ağanın matematik mezunu oğlu Cevdet’e danışmışlar. Her zaman için başarılı eşleştirme yapıp yapamayacaklarını sormuşlar. Cevdet düşünüp taşınmış ve şu teoremi kanıtlamış: “Gençlerin istekleri ne olursa olsun, iki çiftin boşanıp eşlerini değiş tokuş etmek istemeyeceği en az bir eşleştirme vardır.” (s.57)
Heyet bu sonuçtan oldukça memnun kalmış ancak öyle bir an gelmiş ki, liste verenlerin sayısı ve eşleştirmelerin karmaşıklığı yüzünden işin içinden çıkılamaz olmuş. Heyet çalışmalarını bir türlü sonlandıramadığı için yeni evlilikler yapılamamış. Bunun üzerine tekrar Cevdet’ten yardım istenmiş. Görüşme neticesinde, Cevdet’in bahsettiği ve bilgisayar denen makinenin satın alınmasına karar verilmiş. Toplanan paralarla şehre gidip bilgisayarı alan Cevdet köye geri döndüğünde, kahvede toplantı yapılmış. Cevdet bu sorunu çözmek için bir yazılım hazırlaması gerektiğini açıklayarak, bir gün süre istemiş. Ertesi sabah köylüler kahveye doluşmuşlar, yazılım beş dakikada evlenecek çiftleri belirlemiş. Tüm köye mutluluk dalgası yayılmış ancak düğün günü hiç unutulmayacak bir olay yaşanmış.
Köyün cadısı, üç ve hatta dört çiftin aralarında anlaşıp eşlerini değiştirmeleriyle daha mutlu evlilikler yapılabileceğini iddia ederek, bunu kanıtlamış. Cadının yönteminde de boşanmaya yer yokmuş, dolayısıyla köylüler onu dinlemişler. Dünyanın parasını harcayıp oğlunu okutan baba bir hayli üzülmüş. Oğlunu karşısına alıp konuşmuş. Cevdet de yeni kanıtladığı teoremden bahsetmiş babasına: “Eş istekleri ne olursa olsun öyle bir eşleştirme vardır ki, bu eşleştirmeye göre evlenilirse eskisi gibi gene boşanma olmaz, ve başka hiçbir eşleştirme erkekleri daha mutlu edemez.” (s.60) Babasının isteği üzerine Cevdet yazılımı güncellemiş, erkekler daha mutlu olmuşlar. Cadı yeniden ortaya çıkana kadar bu düzen devam etmiş.
Aradan geçen zamanda cadı evlenip üç kız çocuğu sahibi olmuş. Kızlar büyümüşler ve evlilik çağına gelmişler. Hazırladıkları listeleri gören anneleri onlara çok kızmış. Cadı, listelerde yapacağı değişiklikler sayesinde iki kızının daha iyi erkeklerle evlenebileceğini göstermiş, üçüncü kızın durumunda bir farklılık olmayacakmış. Tüm köy cadının hile yaparak bilgisayarı aldattığını konuşmaya başlayınca, Cevdet’in babası yine oğlunu çağırıp olayı sormuş. Cevdet bunun üzerine geliştirdiği son teoremi kanıtlamış: “Erkekler hile yaparak kendilerine daha iyi karı sağlayamazlar.” (s.61) Kadınların hile yaptıkları, hileye karışmayanların ise haksızlığa uğradıkları bir durum varmış ancak erkekler hileyle daha mutlu evlilikler yapamıyorlarmış. Ağa haksızlığın doğada da olduğunu söyleyip oğlundan bir şirket kurmasını istemiş. Böylece kadınlara para karşılığında nasıl daha iyi liste hazırlayacaklarını öğreteceklermiş. Cevdet babasının sözünü dinlemiş ve çok zengin olmuş.
Bir evlilik eşleştirmesi örneği (2)
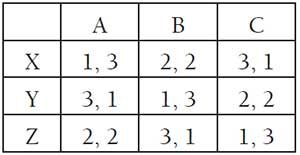Masalsı köyümüzden çıkarak masalsı olmayan tablomuza bakalım. Tablodaki numara çiftlerinde virgülden önceki sayılar erkeklerin, virgülden sonrakiler ise kadınların tercih sırasını vermektedir. X’in ilk tercihi A, ikincisi B ve üçüncüsü C’dir. A’nın ilk tercihi Y, ikincisi Z ve üçüncüsü X’tir. Yukarıdaki tabloya göre 6 farklı eşleştirme yapılabilir. Bunlardan 3 tanesi kararlıdır:
Erkekler tercih listelerinin ilk sıralarındaki kadınlarla, kadınlar tercih listelerinin ilk sıralarındaki erkeklerle ve herkes ikinci tercihiyle eşleştirilebilir.
Diğer üç durum kararsızdır.
Kararlı eşleştirmenin kanıtı
Evlilik probleminde her zaman için kararlı bir eşleştirme yapılabileceği ile ilgili teoremi kanıtlamak için özyineli (dürümsel) yordam (İng. iterative procedure) (3) yöntemine başvuralım.
n tane kadın ve erkek olsun. İlk adımda her erkek en beğendiği kadına evlilik teklifi götürür. Birden fazla erkekten teklif alan bir kadın en beğendiği erkek dışındakileri reddeder ancak ona henüz “evet” demeyip bekleme listesine yazar çünkü daha iyi bir erkekten teklif alma ihtimali vardır. (4) İlk aşamada reddedilen erkekler ikinci tercihlerine teklifte bulunurlar. Kadınlar bu teklifler ve varsa listelerinde bekleyenler arasında bir tercih yapıp gerekirse listelerini güncellerler. Bu işlem böyle devam eder. Bir erkek bir kadına en fazla bir defa teklif götürebileceği için sonuçta her kadın bir teklif alır ve en fazla n2-2n+2 (5, s.26) adımda problem sonuçlanır. Bu eşleştirme için bir örnek düşünelim. A ile B isimli, evli olmayan bir kadın ve erkek seçelim. A mevcut eşi yerine B’yi tercih ediyor olsun. Buradan yola çıkarak A’nın bir aşamada B’ye teklif götürdüğü ve reddedildiği sonucuna ulaşırız. B mevcut eşini A’ya tercih etmiştir. Görünen o ki eşleştirmemiz kararlıdır. Öğrencilerin üniversitelere başvurduğu problem için de aynı çözüm yöntemi kullanılabilir.
Problemimizde erkek ve kadınların sayısının eşit olması gerekmez. n tane erkek ve m tane kadının olduğu bir durumda n < m ise, n adet kadın teklif aldığında işlem sona erer. n > m ise, her erkek bir kadının listesine girdiğinde veya tüm kadınlarca reddedildiğinde süreç tamamlanır. Kadınların teklif ettikleri durumda da problemle ilgili anlatımlar değişmez.
Ele almaya çalıştığımız problemlerin gösterdiği gibi hayatla matematik iç içedir. Sadece evlilikte değil aile içinde, dostluklarınızda ve diğer sosyal ortamlarınızda kararlı ilişkiler dilerim çünkü tablolarımıza en çok (1, 1) yakışıyor.
Not: Alıntılar herhangi bir değişiklik olmadan yapıldı. Konuyla ilgili çalışmalardan haberdar olmamı sağlayan, yorumlarıyla ve sağladığı kaynaklarla bana destek olan, matematikçi Gizem Yıldırım’a teşekkür ederim.
Dipnotlar
1) Ali Nesin, Evliliğin Matematiği, 55-72.
2) Gale, D., & Shapley, L. S., College Admissions and the Stability of Marriage. The American Mathematical Monthly, Vol. 69, No. 1 (Jan., 1962), 9-15.
3) Çeviride Türkiye Bilişim Derneği tarafından hazırlanmış olan bilişim sözlüğünü kullandım: http://www.tbd.org.tr/index.php?sayfa=sozluk&mi1&tipi=entr&harf=A
4) Bahsi geçen yaklaşıma İngilizcede deferred-acceptance denmektedir.
5) Gura, E. Y., & Maschler, M. B., Insights into Game Theory. Cambridge University Press (2008).
