Dünya dönüyorsa neden savrulmuyoruz? Ay neden düşmüyor? Ağırlık sıfır olur mu? Fil ile fare neden aynı anda düşer? Uzay mekiği Dünya’ya dönerken yapay engellemeler olmasa düşene dek hızlanmaya devam eder mi? Dünya’nın ekseni ekliptik düzleme dik olsaydı ne olurdu?.. Milattan önce Apollonius’la başlayıp Kepler’le anlam kazanan, Galileo ve Newton’la doruğa ulaşan uzay yolculuğu devam ediyor.
Apollonius MÖ 262-190 yılları arasında yaşamış. Pergeli Apollonius da deniliyor. Perge Antalya çevresinde eski bir yerleşim alanı. Kültür ve sanatın geliştiği önemli kentlerden. Perge’de doğan Apollonius daha sonra Mısır’ın İskenderiye kentine geçiyor. Bir süre sonra da Bergama’ya. İskenderiye, dönemin en önemli bilim – kültür merkezi. Bergama da bu anlamda önemli merkezlerden biri.
Apollonius’un matematik üzerine birçok çalışması var. Örneğin üç çembere teğet çizme çalışması “Apollonius Problemi” olarak bilinir. En önemli çalışması ise “koni kesitleri” ile ilgili çalışmasıdır. Koninin içinde bir şeyler olduğunu seziyor Apollonius. Koniyi bir düzlemle kestiriyor. Değişik konumlarda oluşan arakesitleri gözlemliyor ve adlandırıyor. Düzlem koninin tabanına paralel ise oluşan şekil çember. Koniyi kesen düzlem koni tabanına paralel değilse (verev) elips, tabanına dik ise hiperbol, ana doğruya (koninin tepe noktası ile taban çemberinin herhangi bir noktasını birleştiren doğru) paralel ise parabol olduğunu görmüş. Bu karşılaştırmayı biraz daha kurcalamış ve arakesitin kâh kesişen iki doğru, kâh paralel iki doğru, hatta bir nokta olduğunu görmüş…
Elips, hiperbol, parabol o güne dek bilinmeyen şekiller değil. Doğada var. Bilinmeyen, bu şekillerin koni ile ilişkisi. Bu ilişkiyi ortaya koymuş Apollonius. Peki, neden yapmış bu incelemeyi? Bu sorunun belli bir yanıtı yok… Kim bilir kaç kişi dudak bükmüştür Apollonius’a, “yapacak işin mi yok” diyerek. Bugün bile bilimle ilgili etkinliklere birçok insan benzer sözleri etmezler mi?
Yaratmak, bulmak, üretmek için “işi olmamak” mı yoksa yaratmanın, bulmanın, üretmenin “kendisinin iş” olması mı tartışması sanırım o gün bugündür sürüyor. Kişinin konumuyla ve niyetiyle ilgili. Ama bulunanların işe yaradığı açık… Bulurken yaşanan süreç ya da bulmaya yönelten itki de önemli. Anlatılır: Küçük bir çocuk kayayı yontan heykeltıraşı görmüş ve sormuş: Sen ne yapıyorsun? Heykeltıraş yanıtlamış, “At yapıyorum.” Anlam veremeyen çocuk dudak bükerek uzaklaşmış. Bir süre sonra aynı yerden geçerken at heykelinin bitmek üzere olduğunu görmüş. Hayretle sormuş. “Sen o taşın içinde at olduğunu nereden anladın?”
Apollonius koni içinde elips olduğunu bilmese de bir şeyler olduğunu seziyordu mutlaka.
Merak, sezgi ve olgular
Eratosthenes MÖ 276-194 yıllarında Yunanistan’da yaşamış. Matematikçi ve astronom. Eski bilimciler genellikle matematikçi ve felsefeci. Bu anlamda her biri birer filozof. Eratosthenes Dünya’nın olgularıyla yetinmemiş. Güneş’i ve gezegenleri gözlemlemiş. Coğrafyanın temellerini atmış, enlem boylam düşüncesini geliştirmiş. Dünya’nın çevresini, yarıçapını hesaplamış.
Yetinmemiş bununla Dünya’nın Güneş’e olan uzaklığını da hesaplamış. Ona da “Dünya’nın Güneş’e olan uzaklığını bilsek ne olur, bilmesek ne olur, işin mi yok” diyenler olmuştur sanırım. Ama o yine de hesaplamış…
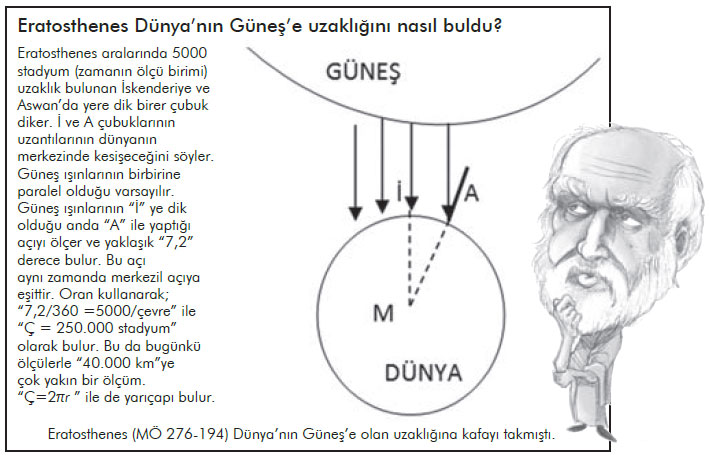
Eratosthenes’in bulgusu Apollonius’un konik kesitleri bulgusundan farklı. Erathosthenes olgulardan yola çıkarken, Apollonius’a sezgileri yön veriyor. Ama ikisi de meraklı, ikisi de kayanın içindeki atı arıyor. İçinde at olduğunu bilse de bilmese de.
İlkel çağlardan beri gökyüzü, yıldızlar, gezegenler, ay, güneş ve bunların hareketi insanların ilgi odağı. Bazen salt merak bazen “dünyadaki yaşamla ilintisi var mı” sorusuyla. Elbette Dünya’nın Güneş’e olan uzaklığı Güneş’e yapılacak bir yolculuk için araştırılmıyor. Ama enlem ve boylamların saptanması fiziksel dünyadaki olayları açıklamak ve yönlendirmek yönüyle anlamlı.
Açıklama ve anlamlandırmada objektiflik sorunu
İster merak ister gereklilik nedeniyle olsun insanın anlama ve anlamlandırma çabası ilkel çağlardan beri tazeliğini korumaya devam ediyor. Bu çaba sonucunda eski çağlarda gözlem ve gözlem sonuçlarına bağlı olarak yoruma dayalı bilgiler üretilmiş. O nedenle birçok kez yanlış sonuçlar da ortaya çıkmış.
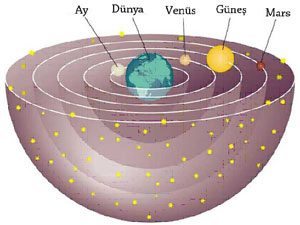Yanlışlardan en bilineni “yer (dünya) merkezli evren” modelidir. Bu model Aristoteles’in evren modeli olarak geçer. Aslında Aristoteles’in ortaya koyduğu model daha genel ve hareketle ilgilidir. Aynı zamanda felsefi… Fiziksel evrene tanrısal anlam yükler Aristoteles. Ona göre evrenin merkezinde dünya vardır. Eflatun da evrenle ilgili Aristoteles’inkine benzer düşünceler ileri sürer. Bu nedenle yer merkezli evren modeli birçok kez Aristoteles-Eflatun modeli diye anılır.
Fiziksel modellemeyi bir sistem olarak yazılı hale getiren ise MÖ 1. yüzyılda yaşadığı sanılan Yunanlı astronom Batlamyus’tur (Ptolemais). Modellemeye göre evrenin merkezinde Dünya vardır. Dünya hareketsiz bir kütledir. Güneş ve Ay, Dünya’nın etrafında dönen cisimlerdir. Her ne kadar MÖ 200 yıllarında yaşayan Yunanlı Aristarchus Güneş merkezli evren modelini ortaya atmışsa da ikna edici olamamıştır.
Gökyüzü-Yeryüzü ve yanlışlar
Dünya merkezli evren modeli en etkili yanlışlardan biri olma özelliğini yüzlerce yıl korudu. Dünya’nın Güneş etrafında dönüyor olması aklın alabileceği şey değildi. İnsanlar kayak yapar gibi dengeleri bozulmadan yerküre üzerinde nasıl duracaktı? Hele de Dünya’nın kendi etrafında dönüyor olması! Dünya dönüyorsa üzerinde bulunan insanlar, nesneler savrulmadan nasıl duracaktı?
Bugün bile bunu anlamak/anlatmak kolay değil. Hele de Dünya’nın dışına çıkıp “işte bak Dünya dönüyor” demenin olanaksız olduğu koşullarda… Yaşanan ama gözlemlenemeyen bir gerçeklik.
Yeryüzünde gözlemlenen olayları doğru yorumlamak da çok kez kolay değildi. Düşme (bugün serbest düşme diyoruz), insanların var oluşlarından beri gözlemledikleri bir olgu. Gözlem sonucunda varılan yargı: “tüm cisimler yere düşer.” Devamında da “hava, gaz, bulut vb. cisim değildir” yargısı. Çünkü onlar yere düşmemektedir! Bir diğer yanlış, Aristoteles’in “cisimler düşerken ağırlıklarına (bugünkü kavrayışımızla kütle) göre hız kazanırlar” tezi. “Aynı yükseklikten düşen (ya da bırakılan) farklı ağırlıktaki iki cisimden ağır olan önce düşer” çıkarımı yüzlerce yıl tartışmasız kabul gördü. Bugün bile sorulduğunda ağır olan önce düşer yanıtı hatırı sayılır ölçüde çoktur.
Harekete ilişkin başka ilginçlikler de gözleniyordu. Örneğin cam (ya da benzeri) üzerinde duran bir cisim camı kırmıyordu. Ancak aynı cisim belirli bir yükseklikten bırakıldığında cam kırılıyordu. Yine herkesin her an görebildiği bir olay, bir gözlem. Düşüşteki şiddet gözlemleniyor ama düşüşün ya da hareketin yarattığı etki ölçülemiyordu. Ölçme araçları olmadığı gibi ölçme düşüncesi de yoktu. Çünkü “deney” bilgiye ulaşmanın yöntemi değildi ve akla bile gelmiyordu. Böyle olunca da deney için gerekli araçlar yapılmıyor ya da yapılamıyordu.
Modern bilimin ayak sesleri
15.- 16. yüzyıla değin süreç böyle işledi. Gözleme, sınama-yanılmaya ve basit ölçmelere bağlı bir süreçti bu. Özellikle hareket alanında. Gezegenlerin ve yerçekiminin yarattığı hareket de bu kavrayışa göre açıklanmaya çalışılıyordu. 1472-1543 yıllarında yaşayan Kopernik Güneş merkezli evren modelini ortaya koydu. Bu model modern astronominin ilk adımı olarak tarihe geçti. Oysa o yıllarda hâlâ Aristoteles ve Eflatun tarafından ortaya konulan “yer merkezli evren” modeli kabul görüyor, okullarda İskenderiyeli Ptolemais’in yazdığı “yer merkezli evren” kuramını esas alan kitabı okutuluyordu. 14 yüzyıl boyunca okutulan bu model belleklere öyle kazınmıştı ki, yerini Kopernik’in Güneş merkezli evren modeline terk etmesi hiç de kolay değildi. Kaldı ki kilisenin öğretilerinde de Aristoteles modeli tanrı yaratısı olarak savunuluyordu. Aksini savunmak yürek işiydi.
Öte yandan Kopernik’in güneş merkezli evren modeli, yer merkezli evren modeline göre çok daha gerçek olmasına karşın eksikleri ve hatta hataları vardı. Kopernik gezegenlerin yörüngelerinin çemberler biçiminde olduğunu söylüyor ve bu yanlış nedeniyle gezegenlerin ve uydularının hareketi tam olarak açıklanamıyordu.
Dönem için daha iyi gözlem olanaklarına sahip olan Kepler (1571-1630) Kopernik’in teorisini geliştirdi. Yörüngelerin, odaklarının birinde güneş olan birer “elips” olduğunu belirledi. Apollonius’un 1800 yıldır atıl olan konik kesitler bulgusu işlevsellik kazanmıştı. Kepler Evren’i “Kepler Yasaları” olarak bilinen üç temel yasaya göre açıkladı. Bunlar:
1) Tüm gezegenlerin yörüngeleri bir odağında Güneş bulunan elipslerdir.
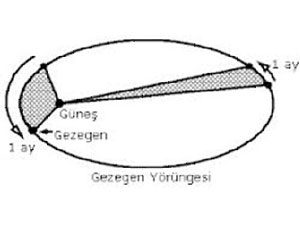
2) Gezegenler eşit zaman aralıklarında eşit alanlar süpürerek hareket ederler. Bu nedenle hızları (yörünge hızı) Güneş’e yakın olduklarında fazla, uzak olduklarında azdır.
3) Bir gezegenin Güneş etrafında dönüş periyotunun karesinin (T2), yörüngesinin (elipsin) büyük eksen uzunluğunun küpüne (R3) oranı sabittir (“T2 / R3 = C”). Bu oran bütün gezegenler için geçerlidir.
Kepler’in ortaya koyduğu yasalar da aslında gözleme dayanıyordu. Giderek gelişen teleskoplar gözlem sonuçlarını daha gerçekçi sonuçlarla açıklasa da inandırıcılık yönü yeterli olmuyordu. Yüzyılların köklü inanışlarını değiştirmek hiç de kolay değildi.
Galileo ve deney
Galileo (1564-1642) da Güneş merkezli evren modelini savunuyordu. Elbette dünyanın kendi etrafında döndüğünü de. Aslında Dünya’nın kendi etrafında döndüğünü anlamak-anlatmak zor değildi. 24 saat içinde gece ve gündüzün yaşanması dünyanın döndüğünün ispatı için inandırıcı bir kanıttı. Dünya kendi etrafında dönmese gece ve gündüz bir dönüş boyunca yani 365 günde birer kez yaşanacaktı. Dünya’nın Güneş’e bakan yüzü gündüz, bakmayan yanı gece olacaktı. Merkezde Güneş de olsa Dünya da olsa bu böyleydi.
Ama en çok karşı çıkışlar kendi etrafında dönen bir kütlenin üzerindeki cisimlerin savrulmadan durmasınaydı. Galileo Pisa kulesinde deneyler yaptı. Öyle ya kulenin tepesinden bırakılan cisim yere inene kadar kule bir yol alacak ve cisim geriye düşecekti. Öyle olmuyor cisim kulenin dibine düşüyordu. İlkel çağlarda bile bazı bilimciler hareket halindeki bir geminin direğinin tepesinden bırakılan cismin direğin dibine düştüğüne ilişkin deneyler yapmıştı. Ve hareket halindeki gemide cisimlerin savrulmadığına ilişkin başka deneyler…
Cisimlerin düşerken ivme kazanması yani hızlanması ile ilgili deneyler de yaptı Galileo. Modellemeyle birleştirerek. Kulenin tepesinden düşen bir cismin saniye saniye hızlanmasını ölçmek (hele o günün koşullarında) olanaklı değildi. İvmelenmeyi kanıtlamak ve ölçmek için eğik düzlemleri kullandı. Sürtünmenin olabildiğince azaltıldığı bir düzlemde yuvarlanmaya bırakılan bilyelerin giderek hızlandığını görmek ve ölçmek daha olanaklıydı. Bu deneylerin sonucu Galileo’yu; “bir cismin düşerken aldığı yol, o yolu almak için geçen zamanın karesiyle orantılıdır” sonucuna götürdü. Modellemeye dayanan bu deneyin matematiksel sonuçlarıyla da kesin bilgiye ulaşıldı. Galileo’nun çalışmalarına sarkaç yasası gibi başka örnekler de verilebilir.
Sonuç olarak söylemek gerekirse Galileo’yla bilime deneyin girmesi ve matematikte analitik yöntemin bulunması bilimin dayanılmaz ağırlığını ortaya çıkardı. “Deneye dayalı” kavrayışlar “inanmaya dayalı” eski kavrayışları zorluyordu. O nedenle adı geçen biliminsanları modern bilimin öncüleri sayılmaktadır. Art arda gelen kuramlar dünyayı, olguları ve hareketi daha gerçekçi kavramaya yol açtı. Bilim gündemine “yerçekimi”, “kütle çekimi”, “serbest düşme”, “kuvvet” gibi yeni kavramlar deneysel ve matematiksel kanıtlarıyla art arda girdi. Ve arkasından Newton’la uzayın ve hareketin kavranması devrimci bir yörüngeye oturdu.
Ve Newton…
MÖ 4. yüzyılda başlayıp 1400’lü yılların sonuna dek hakim olan Aristotelesçi dünya görüşü yıkılıyordu. Kopernik ile başlayan bilimsel devrim aşağı yukarı 200 yıllık bir sürede Newton’la doruğa ulaştı. Newton 1687’de ünlü eseri Principia’yı yayınladı. Okullarda hâlâ Aristotelesçi evren modelinin okutulduğu yıllarda yayınladığı bu eserinde üç temel yasaya indirgediği “dinamik ilkeleri”ni ortaya koydu ve bunları kanıtladı. Bu üç yasa:
1) Üzerinde etki ettirilen kuvvetlerle durumunu değiştirmeye zorlanmadıkça her cisim kendi durgun durumunu, ya da düz çizgi üzerindeki hareket durumunu sürdürür. (Eylemsizlik İlkesi)
2) Hareketteki değişme, etki eden hareket ettirici kuvvet ile orantılıdır. Ve bu değişme kuvvetin etki ettiği düz çizgi doğrultusunda olur. (Dinamiğin Temel Kanunu)
3) Her etkiye eşit bir karşı tepki vardır; ya da, iki cismin birbirleri üzerine karşılıklı etkileri daima eşittir. Ve karşı cisme doğru yönelmiştir. (Etki ve Tepki Yasası)
Kabaca yorumlarsak; yerden 1 metre uzaklıktaki cisim yerçekimi kuvveti (hareket ettirici kuvvet) olmasa havada asılı kalacaktır. Bu cisme bir yönde yere paralel bir itme uygulanırsa sürtünme ve yerçekimi bir yana bırakıldığında itme uygulanan yönde sonsuza dek hareketini sürdürecektir. Yani eylemsizlik yasası. Aynı cisme bir yönde ek bir kuvvet uygulanırsa cisim uygulanan kuvvetin yönü ve şiddeti ölçüsünde hızlanarak harekete devam edecektir. Bu Newton’un ortaya koyduğu ikinci ilkeydi.
Üçüncü yasa yani etki tepki yasası oldukça açıklayıcı. Yere düşen elma yerde durmaya devam eder. Yerin ve elmanın birbirine uyguladığı kuvvetler eşittir. Hareketi (düşmeyi) sağlayan yerin ve elmanın kütleleri arasındaki farktır. Eğer yer çekimi daha az veya daha çok olsaydı yaşadığımız koşullar, davranışlarımız ve belki de bizler bile daha farklı olacaktık. Ama elma yine düşmeye devam edecekti.
Elma neden düşüyor?
Anlatılan, ağacın altında otururken Newton’un kafasına elmanın düşmesi ve Newton’un neden düştü deyip yerçekimini bulduğudur. Hikaye öyle midir, değil midir bilinmez ama bu düşüşe kafa yormuş Newton. Kendisinden önce kafa yoran bilimciler gibi. Çünkü çağlardan beri yüksekten bırakılan cismin ağırlığından daha fazla bir şiddetle düştüğü gözlemlenen bir olguydu. Bu olguyu kargalar bile kullanıyordu. Onlar da düşme şiddetiyle düşme uzaklığının orantılı olduğunu biliyor, aşırdığı cevizi kırmak için belli bir yüksekliğe kadar çıkıp ağzındaki cevizi yere bırakıyor, kırılmadıysa daha yükseğe çıkıp tekrar bırakıyordu. Ancak ne kargalar ne de insanlar bu şiddet artışını biliyor ama şiddetin ölçüsünü bilmiyordu. Ölçme araçları yoktu. Asıl önemlisi ise ölçme-deneme düşüncesi yoktu. Bu nedenle deneyi bilimin merkezine yerleştiren Galileo bilimsel devrimin öncüsü kabul edilir. Daha önce bilgi iknaya dayanıyordu. Ve sanırım bu nedenle güzel konuşma, hitabet, dil becerisi gibi anlamlarda kullanılan “retorik” bilimle birlikte anılan en önemli disiplinlerden biriydi. Deneyin bilime girmesi, sözün yerini alması, bilimin seyrini değiştirdi. Galileo’nun başlattığı süreç yerçekiminden hareketle Newton’un kütle çekim yasasına ulaştı.
Düşmeyle ilgili ilk adımlar Galileo’dan gelmişti. Farklı kütleli cisimler aynı zamanda ama hızlanarak düşüyor ve de düşme şiddetleri kütlelerine bağlı olarak artıyordu. Yani köprüden atlayan fare de fil de hızlanarak (ivmelenerek) ama aynı zamanda düşüyordu. Düştükleri anda ise filin altında olmayı kimse yeğlemezdi. Tüm bu deneysel sonuçlar matematiksel kanıtlar sunulmadan yeterince inandırıcı olamıyordu. Newton kanıtlamalarda matematiği daha yoğun olarak kullanmaya başladı. İşte o zaman; “g” yer çekimi ivmesini, “t” geçen zamanı, “y” alınan yolu göstermek üzere “y = ½ g.t2” bağıntısı ortaya kondu. Bu bağıntı serbest düşmede alınan yolun zamana göre değişimini gösteren evrensel bağıntı. Evrensel diyoruz çünkü Ay’da ya da başka bir gezegende de aynı bağıntı geçerli. Ancak yerçekimi ivmesi dediğimiz “g” farklı gezegenlerde farklı olmak üzere.
Serbest düşme bağıntısını yaratan yerçekimi kuvveti aslında “kütle çekim kuvveti” denilen ve genel anlamda evrende her şeyin yerli yerinde durmasına neden olan temel kuvvet. Elbette yerli yerinde durmaktan hareketsizliği kastetmiyoruz. Yerkürede bize göre yerde duran bir taş hareketsiz… Ya o taşa Ay’a gidip oradan bakan için öyle mi?
Kütle çekim kuvveti
Dünya elmadan büyük ve elmayı kendine doğru çekiyor. Elma da uysal bir kabullenmişlikle bu isteğe uyuyor. Ya dünya küçük elma büyük olsaydı aynı olay gerçekleşecek miydi? Elma, taş gibi toprak gibi dünyanın bir parçası değil mi? Taş, toprak, elma ve yerküredeki tüm nesneler dünyanın merkezine doğru çekiliyorsa merkezde ne vardı? Nesnelerin parçalarını (örneğin taşı oluşturan parçalar, moleküller) yapışık tutan neydi? Bir kaya parçalandıktan sonra neden birleşmiyordu? Ya da bir taş kolayca parçalanabildiği halde bazı taşlar ya da metaller niçin parçalanamıyordu?
Benzer sorularla Newton, çekim kuvvetini salt dünyaya yüklemenin yanlış olacağını düşünmüş olacak ki her iki cismin birbirlerine kuvvet uyguladığını ortaya koydu. Örneğin masanın üzerinde duran bardak o kadar da masum değildi. Yere doğru masayı bir kuvvetle zorluyordu. Masa da ilgisiz kalamıyordu bu meşke. O da bardağa karşı yukarı doğru bir kuvvet uyguluyordu. Öyle ki bu kuvvetler eşit olduğu için bardak masanın üzerinde duruyor, bir anlamda geçinip gidiyorlardı. Daha önce de söyledik. Bardak yerine demir bir gülle, masa yerine de ince camdan bir sehpa seçtiğimizi düşünün… Geçinmek ne mümkün? Cam paramparça, gülle yerlerde… Newton iki cismin birbirini çekmesini ortaya koymakla kalmadı, olgulara dayanarak ispatladı. Daha da önemlisi kütle çekim kuvveti adı verilen bu kuvvet tüm evren için geçerliydi. O nedenle adı “Evrensel Çekim Kanunu”na çıktı. Daha önceki çalışmalarında çekim kanununda çekilen cismin kütlesine yer veriyordu sadece Newton. İşte bu yeni saptamayla iki cismin kütlesini de kullandı.
Kütle Çekim Kuvveti, kütlelerin çarpımı ile doğru, aralarındaki uzaklığın karesiyle ters orantılıdır biçiminde tanımlandı. Yani dünya elmayı çekmek için bir kuvvet uygularken, elma da (kütlesine bakmadan) dünyaya eşdeğer bir kuvvet uyguluyordu. Ve de aynı şey uzaydaki koca koca cisimler için de geçerliydi.
Kütle çekim kuvveti denilen bu kuvvet “ F = G = m.g” bağıntısı ile ifade edildi. Bağıntıda “m” cismin kütlesini (cismin madde miktarını), “g” yerçekimi ivmesini göstermektedir. Örneğin bir bardağın kütlesi Dünya’da ya da Ay’da değişmiyor oysa ağırlık değişiyordu. Değişime neden olan ise Dünya’nın ve Ay’ın yer çekim ivmelerinin farklı olmasıydı. Yer çekim ivmesi de hızdaki değişimin, zamandaki değişime oranı olarak tanımlandı ve matematiksel olarak ortaya konuldu…
Kepler – Newton
Newton’a göre Yer ve elma birbirlerini hangi yasaya göre çekiyorsa Güneş ve gezegenler de aynı yasaya göre çekiyordu. Yani evrenseldi. Newton’un yasaları Kepler’in yasalarından farklı olarak genel hareket yasalarıdır. Evrensel hareket yasaları diye adlandırılan bu yasalar elbette gezegenlerin hareketlerini de kapsıyordu. Newton’un yasalarının diğer üstün yanı ise matematiksel olarak kanıtlanmış olmalarıdır. Öyle olduğu içindir ki Newton’un yasaları geriye dönülmez biçimde uzayın konumuna ve devinimine noktayı koydu. Bu nokta Kopernik’le başlayan sürecin sonucuydu. Bu nedenle Newton, Kopernik, Galileo ve Kepler’i kastederek; “eğer ben uzağı görebilmişsem, devlerin beni omuzlarında taşımış olmasındandır” der.
Gökyüzü ve gökyüzündeki hareket en ilkel çağlardan beri insanlığın ilgi odağı olmuştur. Nasıl olmasın ki? Engin maviliği ile coşturan, yıldırımı ile korkutan, yağmuru ile umutlandıran, buzu ile üşüten… başka ne ola ki? En çok da hareketinin gizemi çekiciliğini hep korumuştur. Ama ürkekliğini de! Gizemin olduğu yerde dogmatik düşünüşün olması da kaçınılmazdı elbette. Bu nedenle gökyüzünün ürkütücü gizemi tanrısal yaptırımlardan, falcılığa kadar birçok alana kapı açmıştır.
Gizemli tur
Kepler’in gözleme ve yoruma dayalı olarak ortaya koyduğu “Gezegenlerin yörüngelerinin elips biçimli olduğunu ve eşit zaman aralığında eşit alanlar süpürdüğü” saptamasının Newton tarafından kanıtlandığını söylemiştik. Ama nasıl? Newton “gezegen A’dan B’ye ve B’den C’ye eşit zaman aralığında yol alıyorsa taradıkları alanlar eşittir” iddiasını nasıl kanıtlamıştı?
Bunun için ardışık iki eşit zaman aralığında gezegenin aldığı yolları karşılaştırmakla başlayalım. Ve aşama aşama harekete etki eden unsurları ele alalım.
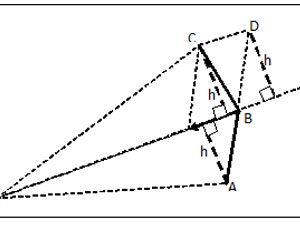
A noktasındaki gezegenin bir zaman aralığında B noktasına gittiğini düşünelim. Eylemsizlik ilkesi nedeniyle aynı zaman aralığında D noktasına ulaşması beklenir ki; lBDl yolu lABl yoluna eşit olacaktır. Ancak B noktasındayken Güneş’in (G) çekim kuvveti nedeniyle yolu lBCl biçimine dönüşecektir. Üç köşesi B, C, D olan dördüncü köşesini adlandırmadığımız dörtgenin paralelkenar olduğu ve paralelkenarın köşegeni olan lBCl uzunluğunun lAB=lDBl’den küçük olduğu açıktır. Paralelkenar özelliğinden C ve D noktalarından indirilen dikmelerin eşit olacağı da açıktır. Diğer yandan lABl ve lDBl hipotenüslü dik üçgenler de eş üçgenlerdir. Bu nedenle A noktasından indirilen dikme de D noktasından indirilen dikmeye eşittir ki; bu dikmeler lGBl tabanlı AGB ile CGB üçgenlerinin yükseklikleridir.
Bu durumda yükseklikleri eşit olan lGBl tabanlı AGB ile CGB üçgenlerinin alanlarının eşit olduğunu söyleyebiliriz. Yani gezegen eşit zaman aralığında daha az yol aldığı halde eşit alan süpürmektedir.
Aslında biz söylemiyoruz. Bu kanıt 1600’lü yıllarda Newton’un ortaya koyduğu matematiksel ve geri dönüşsüz mükemmel bir kanıt. Kepler’in gözleme dayalı bulgusunun matematiksel kanıtı. Elbette inceleme çok daha kapsamlı. Bu kanıt ayrıntılarıyla (ve kendi katkılarıyla) yakın tarihin büyük fizikçilerinden Richard Feynman (1918-1988) için yazılan ve TÜBİTAK yayınlarından çıkan “Feynman’ın Kayıp Dersi” adlı kitapta anlatılmaktadır.
Bu kanıtın ardından da gezegenin eşit zaman aralığında (örneğin 1 ay) Güneş’e yakınken taradığı alanla uzakken taradığı alanlar eşittir. Yakınken aldığı yol ise uzakken aldığı yoldan daha fazladır. Sanırım artık gezegenin yörüngede hareket ederken hızlanıp yavaşlamasını kanıtlamaya gerek kalmadı.
Ay neden düşmüyor? Ya da savrulmuyor?
Bilim Ay’ın Dünya’nın uydusu olduğunu açıklıyor. Bu dönüşün nedenini de dünyanın çekim kuvvetine bağlıyor. Ama karşı çıkışlar da başlıyor… “Dünya Ay’ı çekiyorsa Ay neden düşmüyor?” Bunu söyleyen içinden “iyi ki de düşmüyor” diyordur elbette. Ya da düşecek seviyede çekemiyorsa neden uzay boşluğuna savrulup gitmiyor? Yanıt yine bilimden geliyor.
Bu denge olmasa Ay’ın Dünya etrafında dönüşü düzenli ve dengeli olmazdı. Ya savrulma kuvveti ağır basar eylemsizlik ilkesi nedeniyle yatay kuvvet yönünde savrulur kaybolur giderdi. Ya da yer çekimi ağır basar Dünya’nın merkezine doğru düşüş Dünya’ya çarpmasına neden olurdu. Bizim için de tartışılacak kafa yorulacak bir şey kalmazdı. İşte bu savrulma-düşme dengesinin yarattığı aşk, Ay’ın Dünya etrafında biteviye dönmesini sağlıyor. Düşmeden ve savrulmadan…
Milattan önce Apollonius’la başlayıp Kepler’le anlam kazanan, Galileo ve Newton’la doruğa ulaşan uzay yolculuğu devam ediyor. Uzaya ilk yolculuğu yapan Sovyet uzay adamı Yuri Gagarin, Ay’a ilk ayak basan Amerikalı Neil Armstrong ve günümüzde Kızıl Gezegen’e yapılan yolculuklarla… Ve de yeni sorularla: Hâlâ neden savrulmuyoruz, Ay neden düşmüyor, ağırlık sıfır olur mu, fil ile fare neden aynı anda düşer, uzay mekiği Dünya’ya dönerken yapay engellemeler olmasa düşene dek hızlanmaya devam eder mi, Dünya’nın ekseni ekliptik düzleme dik olsaydı ne olurdu vb.
Son sözümüz eğitimle ilgili. Yukarıda söz ettiğimiz şeyler aşağı yukarı lise öğrenimi boyunca öğrencilere anlatılan konulardır. Matematik, Fizik, Coğrafya derslerinde. Ancak bu sorulara ya da benzer sorulara çoğunlukla doğru yanıtlar alamayız. “Ocak ayında mı Dünya Güneş’e daha yakın, Temmuz ayında mı” sorusunu sorun ve deneyin. Bu denli merak duyulan bir alanı bile öğrenilemez duruma getirmek eğitimin içerik ve yöntem sorunu değilse nedir? Nedenleriyle ortaya konmayan bilginin kalıcılığı yetersizdir. Ne yazık ki öğrenme yöntemi ya da bilgiye sahip olma yöntemi genellikle ansiklopedik yaklaşımla olmaktadır. Yani nedenleri ortaya konulmadan ve de ezberlenmesi istenerek. Elbette bilgi aktarımı bir öğrenme yöntemi. Ancak kalıcı olmayan, unutulmaya hazır bir öğrenme yöntemi. Okullardaki öğretimde “neden öğrenemiyorlar” yakınmasının temel nedenlerinden biri bu. Öğrenciler için bilgi; hesabı verilecek, unutulmaya hazır “beyin ve duygu yükü…”
