Bu yazıda basit ama oldukça ilginç bir yazı tura oyununu ele alıyoruz. Bu oyunu kumarhaneye karşı oynar mısınız, yani “uzun vadede” kazanabilir misiniz? Bu soruyu sıra dışı, şık bir çözümle sezgilerimizden bağımsız olarak yanıtlayacağız. Çözüm, matematiksel yaratıcılığın sürpriz zarafetine güzel bir örnek. Meraklı okurun ilgisini çekeceğini umuyorum.
Dokuz atışta yazı tura oyunu. Oyuncu yazı ya da turadan birini seçtiğini açıklar ve hilesiz bir madeni parayı dokuz kez atar. Diyelim ki oyuncu yazıyı seçti. Oyun boyunca her atış sonrası yazıların sayısı turaların sayısından büyükse oyuncu kazanır, ortaya koyduğu her 10 lira için 60 lira alır. Eğer her atış sonrası yazıların sayısı turaların sayısından küçük ya da eşitse oyuncu ortaya koyduğu 10 lirayı kaybeder.
Oyuncunun kazanma olasılığı ve beklenti sayısı kaçtır?
Çözüm. Önce, her atış sonrası yazıların sayısının turalardan büyük olmasını dikkate almayalım. Bu durumda dokuz atış sonunda yazı sayısının tura sayısından fazla olduğu olası seçenekler şunlardır: 9 yazı 0 tura, 8 yazı 1 tura, 7 yazı 2 tura, 6 yazı 3 tura, 5 yazı 4 tura.
Şimdi, yukarıdaki beş seçenekten birini ele alalım, örneğin 6 yazı 3 tura. Bu durum için sorunun bizden istediği olasılığı bulmaya çalışacağız, daha sonra aynı yöntemle diğer seçenekleri de hesaplayıp oyuncunun kazanma olasılığına ulaşacağız.
Dokuz atışta 6 yazı 3 tura gelme olasılığını hesaplamak oldukça basit: mümkün haller sayısı 29=512 , uygun haller sayısı 9’un 6’lı kombinasyonu, ve 6 yazı 3 tura gelme olasılığı 84/512.
Tabii ki bulmak istediğimiz olasılık yukarıdaki sonuç değil, çünkü biz her atış sonrası yazı sayısının tura sayısından fazla olmasını istiyoruz. Bunun için 84 seçenek içinden istemediğimiz durumların sayısını çıkarırsak geriye her atış sonrası yazıların sayısının turaların sayısından büyük olduğu durumlar kalacak.
Akıl dolu bir hamle: Şah mat!
Az sonra istemediğimiz durumların sayısını akıl dolu bir yolla bularak probleme beyaz bayrak sallatacağız.
Yazıların daima önde gidebilmesi ilk iki atışta yazı gelmesine bağlı, çünkü (YT), (TY) veya (TT) gelmesi durumunda oyuncu kaybediyor, kumarhane kazanıyor.
Şimdi, 6 yazı 3 tura içinden rastgele bir durumu ele alalım. Örneğin (YYTTTYYYY) seçeneğine bakalım: Oyuncu kaybeder, çünkü dördüncü atışta yazı sayısı tura sayısına eşit oluyor.
Bu aşamaya dikkat! Sayıları geometriyle buluşturuyoruz. Her bir atış için koordinat düzleminde göstereceğimiz noktaların bileşenlerini belirleyeceğiz. Şöyle ki: Birinci bileşen atış sayı, ikinci bileşense her atış sonrası yazıların turalardan ne kadar fazla ya da eksik olduğunu gösteren sayı olacak. Örneğin beş atışlık (YYTTT) durumuna karşılık gelen beş noktanın ilki (1, 1) olur çünkü atış sayısı 1, yazı sayısı 1. Aynı şekilde ikinci nokta (2, 2), üçüncü (3, 1), dördüncü (4, 0), beşinci nokta (5, -1). Dikkat edilirse, dördüncü atış sonunda yazı sayısı tura sayısından çıkarılırsa sonuç sıfır olduğundan dördüncü noktanın ikinci bileşeni sıfır oluyor. Aynı şekilde beşinci atış sonrasında yazılar turalardan çıkarıldığında elde edilen sonuç -1, beşinci noktanın ikinci bileşeni oluyor.
Şimdi, yukarıda rasgele seçtiğimiz (YYTTTYYYY) durumuna bir kez daha bakalım ve dokuz atış için dokuz noktayı sırasıyla belirleyelim: (1, 1), (2, 2), (3, 1), (4, 0), (5, -1), (6, 0), (7, 1), (8, 2), (9, 3).
Yukarıda belirlediğimiz dokuz noktayı koordinat düzleminde gösterip, bu noktaların birleştirilmesinden oluşan grafiği çizelim.
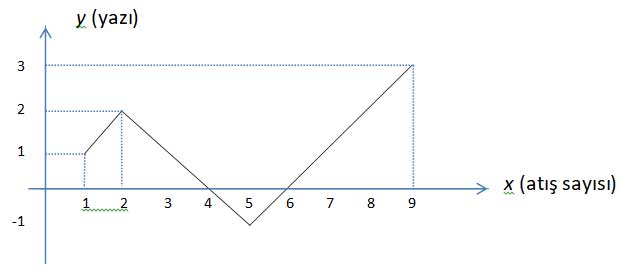
Oyuncunun kazanabilmesi için grafiğin (1, 1) noktasından başlayıp (9, 3)’te bitmesi gerekiyor, ama bu yeterli değil, ayrıca grafiğin x eksenini kesmemesi (ikinci bileşen negatif olduğunda turalar yazılardan çok oluyor), hatta x eksenine uğramaması gerekiyor ( ikinci bileşen sıfır olduğunda yazı sayısı tura sayısına eşit oluyor, oyuncu kaybediyor). O halde biz (1, 1)’de başlayıp (9, 3)’de biten ve x eksenini kesmeyen grafiklerin sayısını bulmalıyız.
Öte yandan 6 yazı 3 turaya karşılık gelen toplam 84 tane grafiğin olduğunu biliyoruz. Bu 84 grafiğin başlangıç noktası (1, 1) ya da (1, -1) olacak. Oyunun her aşamasında yazıların önde olması için başlangıç noktası (1, 1) olmalıdır elbette.
(1, 1)’den başlayıp x eksenine uğrayarak (9, 3)’e giden grafiklerin sayısıyla (1, -1)’den başlayan (9, 3)’e giden grafiklerin sayısını toplayıp 84’ten çıkarırsak x eksenine uğramadan (9, 3)’e giden grafiklerin sayısını bulmuş olacağız.
Önce, (-1, 1)’den başlayıp (9, 3)’e giden grafiklerin sayısını bulalım: Bir grafik (-1, 1)’den başladıysa ilk atış tura gelmiş demektir. Grafiğin (9, 3)’e gidebilmesi için ilk atıştan sonraki sekiz atışın altısının yazı ikisinin tura olması gerekiyor. O halde (-1, 1)’den başlayıp (9, 3)’e giden grafiklerin sayısı ’dir.
Şimdi de (1, 1)’den başlayıp x eksenine uğrayarak (9, 3)’e giden grafiklerin sayısını bulalım. Bu sayı da 28, yani (-1, 1)’den başlayıp (9, 3)’e giden grafiklerin sayısına eşit! Hoş bir sürpriz! Şöyle ki: Yukarıda grafiğini çizdiğimiz (YYTTTYYYY) seçeneğinde yazıları tura, turaları yazı yaparsak (TTYYYTTTT) olur. Bu durumun grafiği aşağıdaki gibidir.

İlk grafikle yukarıdaki karşılaştırılırsa grafiklerin x eksenini ilk uğradıkları noktanın solunda birbirlerinin x eksenine göre simetriği oldukları görülür. O halde her bir seçenek için yazıları tura, turaları yazı yaparsak (-1, 1)’den başlayıp (9, 3)’e giden grafiklerin sayısıyla (1, 1)’den başlayıp x eksenine uğrayarak (9, 3)’e giden grafiklerin sayısının eşit olduğu görülür. Böylece (1, 1)’den başlayıp x eksenine uğramadan (9, 3)’e giden grafiklerin sayısı 84 – 28 – 28 =28 olur.
Artık istediğimiz olasılığı, yani dokuz atış boyunca yazı sayısının tura sayısından büyük olma olasılığını bulabiliriz: 28/512.
Bundan sonra, diğer durumlar ( 9 yazı 0 tura, 8 yazı 1 tura, 7 yazı 2 tura, 5 yazı 4 tura) için de aynı yöntemle olasılıkları hesaplayabiliriz.
5 yazı 4 tura için istenilen olasılık, (9, 5) – 2 x (8, 5) / 29=14/512
olur. Aynı şekilde hesaplanırsa, 7 yazı 2 tura için 20/512, 8 yazı 1 tura için 7/512, 9 yazı 0 tura için 1/512 bulunur.
Başlangıçtaki 6 yazı 3 tura için bulduğumuz 28/512 sayısıyla yukarıdaki sayıları toplarsak oyuncunun kazanma olasılığını buluyoruz: 28+14+20+7+1/512=35/256
Dokuz atış boyunca yazıların sayısının turaların sayısından büyük olma, yani oyuncunun kazanma olasılığı 35/256. Kaybetme olasılığı ise 1-35/256 = 221/256 olur.
Şimdi, beklenti sayısını bularak bu oyunun uzun vadede kazanılıp kazanılamayacağına karar verelim.
Oyuncu kazandığında ortaya koyduğu her 10 lira için kumarhaneden 60 lira alıyor. Bu durumda oyunun beklenti sayısı: 35/256 x 60 – 221/256 x 10 = -55/128
Beklenti sayısı negatif çıktı, oyuncu kaybeder, oynamamalı!
Düzeltme: Geçen sayıdaki yazıda sayfa 76’daki eşitlikte 5/8 yazılmış, -5/8 olmalı. Ayrıca sayfa 77’de P(z)+P(z)=1 yazılmış, P(z)+P(g)=1 olmalı. Teknik nedenlerden kaynaklanan bu düzeltmeler için özür diliyoruz.