Ünlü Alman filozof Nietzsche’nin “Tanrı öldü” sözüyle bilimsel gelişmeler sonrasında Tanrıya ihtiyaç kalmadığını anlatmak istediği söylenebilir. Nietzsche’nin böylesi bir sonuca varmasındaki en önemli iki gelişme, Newton’un matematiksel fiziği, Darwin’in canlı türlerinin kökenini keşfetmesi olarak sayılabilir.
Doğal dünyayı anlamada en etkili yol olan matematiksel fizik bütünüyle türev ve integralleri konu eden diferansiyel hesaba dayanır. Diferansiyel hesabın öncüleri addedilen Newton ve Leibniz’in yaşadığı 17’inci yüzyılı izleyen yüz elli yıl içinde bu alanda çok hızlı ilerlemeler yaşandı. Doğanın birçok yasası türev ve integral hesabın diliyle yazıldı. Türev ve integraller, kabına sığmaz bir aşkınlıkla fizik, astronomi, mühendislik gibi alanlarda uygulanarak yeni buluş ve yöntemlerin ortaya çıkmasını sağladı, ama bu üretken süreç beraberinde bazı sorunların, belirsizliklerin ve zayıflıkların oluşmasına da neden oldu. Diferansiyel hesabın yapısındaki çelişkilere karşın doğadaki uygulamalarında elde edilen olağanüstü başarılar kanıt ve kavramlardaki bulanıklığı gizliyordu.
Diferansiyel hesabın inşasında yer alan “sonsuz küçük” kavramına ilk eleştiri, daha doğrusu ilk saldırı 1734’de İrlandalı piskopos George Berkeley tarafından yapıldı. Berkeley, The Analyst(Analizci) isimli kitabında sonsuz küçükleri “yok olmuş niceliklerin hayaletleri” olarak niteledi. Aslında Berkeley’in bu kitabıyla Newton’un arkadaşı ve Halley kuyruklu yıldızının isim babası olan astronom Edmund Halley’i hedef aldığı tahmin edilir. Halley ateisttir ve Berkeley’in bir arkadaşını dinin imkansızlığı konusunda ikna etmiştir. Belki Berkeley Halley’den intikam alıyordu ve belki sonrasında Nietzsche’nin dediği gibi “Tanrı öldü” denilmesinden korkuyordu, ama öne sürdüğü matematiksel eleştiriler son derece doğruydu.
Sonsuz küçük kavramındaki sorun neydi? Newton ve Leibniz’in kullandığı sonsuz küçük kavramını basite indirgeyerek şöyle açıklayabiliriz: Bütün pozitif sayılardan küçük ama sıfırdan büyük bir sayı! Böyle bir sayı bulabilir miyiz? Elbette bulamayız, çünkü bir sayı sıfır olmaksızın ne kadar küçük olabilir ki? “Sonsuz küçük” adını verdiğimiz sayıyla sıfır arasında hiçbir sayının olmaması gerekir ki bu mümkün değildir, çünkü “sonsuz küçüğün” yarısını alarak daha küçük bir sayı ve bu işleme devam ederek daha da küçük sayılar elde edebiliriz. Bu küçültme işlemlerini yaparak sıfıra çok yakın sayılar bulabiliriz, ama “en küçük sayı şu” veya “sonsuz küçük sayı şu” diyemeyiz.
Yolum yanlış ama sonuç doğru…
Öğrenciliğimizde bir matematik problemini çözerken çok sık karşılaştığımız bir durumdur, şöyle söyleriz: “Yolum yanlış ama sonuç doğru”. Matematik tarihinde sonsuz küçüklerle yapılan işlemlerde de tam böyle olmamakla birlikte benzer bir süreç yaşandı. Sonsuz küçükleri kullanarak doğru sonuçlara ulaşılıyordu ama gidilen yol belirsizdi. Bu durumu geometriden bir örnekle açıklayalım, sonra türev ve integraldeki sonsuz küçük kullanımını ele alalım.
Bir dairenin alanın sayısal değerinin çevresinin sayısal değerine oranının yarıçap uzunluğunun yarısına eşit olduğunu biliyoruz. (πr2/2πr = r/2). Bu eşitliği şu yöntemle kanıtlamaya çalışalım. Dairenin içine sonsuz sayıda yarıçap çizdiğimizi varsayalım ve yarıçapları yüksekliği r olan sonsuz küçük üçgenler gibi düşünelim. Aşağıdaki şekilde çizilmiş olan yarıçapların sonsuz sayıda olduğunu ve daireyi kapladığını hayal edelim.
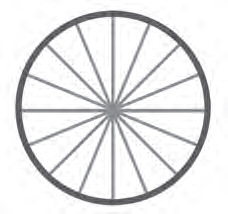Böylece daire her birinin yükseklik uzunluğu r birim olan sonsuz küçük üçgenden oluşmaktadır. Bir üçgenin alanı taban uzunluğuyla o tabana ait yükseklik uzunluğunun çarpımının yarısına eşit olduğundan üçgenlerin alanlarının toplamı taban uzunluklarının toplamıyla r’nin çarpımın yarısına eşit olacaktır. Taban uzunluklarının toplamı da dairenin çevre uzunluğuna eşit olduğundan üçgenlerin alanları toplamı yani dairenin alanı, çevresinin r/2 katına eşit olur.
Bu sonuç elbette doğrudur, ama sonuca giderken atılan adımlar oldukça sorunludur. Bir üçgenin sonsuz küçük tabanı olabilir mi? Sözü edilen üçgenlerin taban uzunlukları sıfır değilse (ki sıfır olamaz çünkü o zaman üçgenden söz edemeyiz) ne kadar küçük olurlarsa olsunlar taban uzunluklarından oluşan sonsuz sayıda terimi topladığımızda sonsuz büyüklükte bir toplam buluruz. Bu itiraz matematikte Arşimet özelliği olarak bilinen, sıfırdan büyük çok küçük bir sayının bile kendisiyle “defalarca” toplanması halinde sonlu bir büyüklüğe ulaşılacağı önermesine dayanır ki, burada sonsuz küçükler sonsuz sayıda toplandığından sonsuz büyüklükte bir toplama ulaşmamız gerekirdi.
Newton, türevi keşfederken bir eğri boyunca hareket eden ve hızı sürekli değişen bir cismin anlık hızının ne olacağı sorusuna yanıt aramıştır. Bu hesabı basitçe açıklayabilmek için bir örnek verelim. Düşen bir taşın s = t2 parabolü üzerinde hareket ettiğini varsayalım ve verili bir andaki, mesela t = 1 anındaki hızını hesaplamaya çalışalım. Burada s, taşın kat ettiği yolu, t de taşın bırakılmasından itibaren geçen zamanı gösteriyor.
Sonlu bir zamanda ortalama hızı hesaplarken kullandığımız, ortaokuldan bu yana bildiğimiz bir formül var: Hız = Yol Zaman. Acaba t = 1 anındaki hızı bu formülle bulabilir miyiz? Şöyle yapalım: t = 1 anından sonra geçen sonsuz küçük bir zaman olduğunu varsayalım ve bu sonsuz küçük zaman artışını da dt simgesiyle gösterelim. Bu durumda cismin t = 1 ile t = 1+dt zamanları arasında alacağı yolu eşitliğiyle hesaplayabiliriz: (1+dt)2–12 = 2dt+dt2.
Zamandaki sonsuz küçük artış, yolda da sonsuz küçük bir artışa karşılık gelecektir. Yukarıda hesaplanan yoldaki sonsuz küçük artışı da simgesiyle gösterelim. Şimdi, Hız = Yol / Zaman formülüyle sonlu olması gereken ds/dt oranını bulalım.
ds/dt = 2dt+dt2 / dt = 2+dt
Bu oran sonlu olması gerektiğinden sonsuz küçük bir terim olan dt’yi atar ve t = 1 anındaki anlık hızın değerini 2 olarak buluruz.
İtiraz fırtınası…
İşte, tam burada Berkeley’in itiraz fırtınası şöyle başlar: “Ne kadar küçük olursa olsun bir şey ihmal ediliyorsa, hızın kesin değere değil ancak yaklaşık bir değere sahip olduğunu söyleyebiliriz. (…) Artışların yok olduğunu varsayıyorsak, artışların var olduğu yönündeki ilk varsayım terk edilmiş demektir, bu durumda o ilk varsayımın sonuçlarından biri sayesinde elde edilmiş bir sonuçla karşılaşırız ki bu da yanlış bir akıl yürütmedir. Peki, bu anlık sonsuz küçük artışlar nedir? Bunlar ne sonlu niceliklerdir, ne de hiçliktir. Bunlara ölmüş niceliklerin hayaletleri dememiz gerekmez mi?”
Berkeley’in tepkisini yukarıda verdiğimiz örneğe göre şöyle özetleyebiliriz: Eninde sonunda, dt ya sıfıra eşittir ya da sıfıra eşit değildir. Eğer dt sıfıra eşit değilse 2+dt de 2’ye eşit değildir, eğer dt sıfıra eşitse mesafedeki ds artışı da sıfıra eşit olur ki bu durumda dt/ds oranı da 2’ye eşit değil, 0/0 gibi anlamsız bir ifadeye eşit olur.
Berkeley’in türev ve integralin mantıksal temellerine yönelik eleştirileri doğruydu. Acaba bu görkemli yapı çökecek miydi? Hiç de beklendiği gibi olmadı; matematikçiler, fizikçiler, mühendisler bir yüzyıl daha üstelik büyük bir başarıyla sonsuz küçüklere dayanan türev ve integrali kullanmaya devam ettiler. Sonsuz küçükler kavramı şüphe ve tepki çekse de mükemmel ve “doğru sonuçlar” elde edildiğinden türev ve integral hesaba olan güvenin sarsılmadığını söyleyebiliriz. Newton ve Leibniz’in yöntemlerinin tarihsel önemine büyük bir değer biçen Karl Marx, sonsuz küçükler krizi üzerine Matematiksel Elyazmaları’nda şu notu düşmüştür: “Matematikçiler, doğru sonuca yanlış bir matematiksel işlemle varan yeni bulunmuş hesaplama aracının gizemli karakterine gerçekten güvendiler”.
Bu krizden çıkmak için yaklaşık yüz yıl gibi bir sürenin geçmesi gerekiyordu. Soyut matematik ayrı bir disiplin olarak ortaya çıktığında matematikçiler türev ve integralin temellerinde hiçbir çelişki olmadığına emin oldular. Bugünkü limit kavramını 1916’da Bolzano, 1821’de Cauchy birbirlerinden bağımsız olarak keşfederek sonsuz küçük kavramının türev ve integral hesabının içinden atılmasını sağladılar. 1870’lerde Alman matematikçi Weierstrass, limitin “delta-epsilon” tanımını yaparak türev ve integral hesabın sarsılmaz biçimde temellerini atmış oldu.
Weierstrass’ın limit tekniğini kullanarak anlık hızı bulurken, hızı bir oran olarak değil bir limit, sonlu artışların oranlarıyla yaklaştığımız bir limit olarak ele alırız. Diyelim ki, Δt simgesi değişken bir sonlu zaman artışını, Δs simgesi de değişken mesafe artışını göstersin. Bu durumda Δs/Δt, 2+Δt değişken niceliğine eşit olacaktır. Δt’yi limit durumunda sıfıra yakalaşırken Δs/Δt’nin de 2 değerine yaklaştığını ve tanım itibariyle t = 1’deki hızın tam olarak 2 olduğu sonucuna ulaşırız. Bu attığımız adımlar sadece bir açıklama olup, meraklı okura daha derinlemesine bilgi için Kaynak 3’ü incelemesini öneririm.
Sonuç olarak, sonsuz küçükler krizi 19’uncu yüzyılın ikinci yarısında tamamen aşılmakla birlikte, her matematiksel krizin sonrasında olduğu gibi matematik dünyasında parlak keşiflerin yapılmasına ön ayak oldu ve tarih Newton’la Leibniz’i haklı çıkardı. Bu süreci matematik tarihçisi Judith Grabiner’in şu sözleri çok iyi açıklar: “Türev ilk önce kullanıldı, sonra keşfedildi, daha sonra araştırılıp geliştirildi ve en sonunda tanımlandı”.
Kaynaklar
1) Ian Stewart, Matematiğin Kısa Tarihi, Çev. Sibel Sevinç, Alfa yayınevi, 2016.
2) Philip J. Davis, Reuben Hersh, Matematiğin Seyir Defteri, Çev. Ender Abadoğlu, Doruk yayınevi, 2009.
3) Ali Nesin, Analiz I-II, NMK E-Kütüphane- Nesin Matematik Köyü.
4) Karl Marx, Matematiksel Elyazmaları, Çev. Öner Ünalan, Başak yayınevi, 1990.
